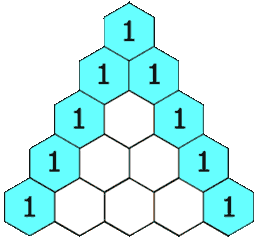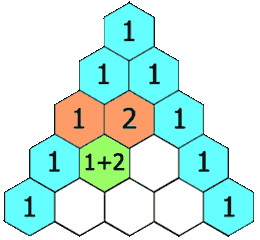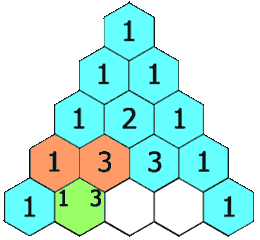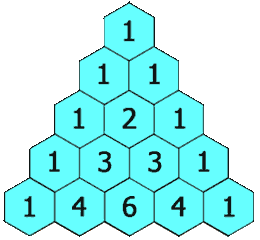
给定一个非负整数 numRows,生成杨辉三角(在杨辉三角中,每个数是它左上方和右上方的数的和。)的前 numRows 行。
示例:
输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
来源:力扣(LeetCode)
链接: https://leetcode-cn.com/problems/pascals-triangle
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路:
如果能够知道一行杨辉三角,我们就可以根据每对相邻的值轻松地计算出它的下一行。
所以要计算第n列的元素,需要从头开始
如下:
class Solution {
public List> generate(int numRows) {
List> resultlist=new ArrayList<>();
if (numRows == 0){//如果等于0直接返回
return resultlist;
}
resultlist.add(new ArrayList<>());
resultlist.get(0).add(1);//添加根元素
for (int i = 1; i nowList=new ArrayList<>();
List pre=resultlist.get(i-1);
nowList.add(1);//默认在每一列第一位为1
for (int j = 1; j 杨辉三角II
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角(在杨辉三角中,每个数是它左上方和右上方的数的和。)的第 k 行。
示例:
输入: 3
输出: [1,3,3,1];
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/pascals-triangle-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路:既然上面的可以把所有的元素都拿到,这次只拿他要求的k行就可以了,如下:
//第K行的元素
class Solution {
public List getRow(int rowIndex) {
List> resultlist=new ArrayList<>();
resultlist.add(new ArrayList<>());
resultlist.get(0).add(1);
if (rowIndex==0){
return resultlist.get(0);
}
for (int i = 1; i <=rowIndex ; i++) {//先获取每一行的list,然后塞进总list里
List nowList=new ArrayList<>();
List pre=resultlist.get(i-1);
nowList.add(1);
for (int j = 1; j 会发现这中效率不高,看题解中有用数学方式解决的:
首先我们应该了解杨辉三角正好是二次项的展开式,(1+x)的n次幂的系数,有通项公式C(n-1,m-1)=(n-1)!/[(m-1)!(n-m)!] 而研究每一项后,发现他们的规律,如 C(4,1)=C(4,0)4/1,C(4,2)=C(4,1)3/2,
C(4,3)=C(4,2)2/3,C(4,4)=C(4,3)1/4:
找到规律,所以0ms的大神代码才写成如下这样子:
作者:a-lan-ruo-2
链接:https://leetcode-cn.com/problems/two-sum/solution/yang-hui-san-jiao-de-tong-xiang-gong-shi-by-a-lan-/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
//第K行的元素
class Solution {
public List getRow(int rowIndex) {
List res = new ArrayList(rowIndex+1);
long nk = 1;
for(int i = 0; i <= rowIndex; i++){
res.add((int)nk);
nk = nk * (rowIndex - i) / (i + 1);
}
return res;
}
}
每天一算法,成功有方法,坚持!
原文链接:
杨辉三角:https://leetcode-cn.com/problems/pascals-triangle/
杨辉三角II:https://leetcode-cn.com/problems/pascals-triangle-ii/