几乎所有的深度学习框架背后的设计核心都是张量和计算图,PyTorch也不例外,本章我们将学习PyTorch中的张量系统(Tensor)和自动微分系统(autograd)。
3.1Tensor
Tensor,又名张量,读者可能对这个名词似曾相识,因为它不仅在PyTorch中出现过,也是Theano、TensorFlow、Torch和MXNet中重要的数据结构。关于张量的本质不乏深度剖析的文章,但从工程角度讲,可简单地认为它就是一个数组,且支持高效的科学计算。它可以是一个数(标量)、一维数组(向量)、二维数组(矩阵)或更高维的数组(高阶数据)。Tensor和numpy的ndarray类似,但PyTorch的tensor支持GPU加速。
本节将系统讲解Tensor的使用,力求面面俱到,但不会涉及每个函数。对于更多函数及其用法,读者可通过在IPython/Notebook中使用
In : from __future__ import print_function
import torch as t
3.1.1 基础操作
学习过numpy的读者会对本节内容非常熟悉,因为tensor的接口设计得与numpy类似,以方便用户使用。若不熟悉numpy也没关系,本节内容并不要求读者先掌握numpy。
从接口角度讲,对tensor的操作可分为两类:
(1)torch.function,如torch.save等。
(2)tensor.function,如tensor.view等。
为方便使用,对tensor的大部分操作同时支持这两类接口,在本书中不做具体区分,如torch.sum(a,b)与a.sum(b)功能等价。
从存储角度讲,对tensor的操作又可以分为两类:
(1)不会修改自身的数据,如a.add(b),加法的结果会返回一个新的tensor。
(2)会修改自身的数据,如a.add_(b),加法的结果仍存储在a中,a被修改了。
函数名以下划线结尾的都是inplace方式,即会修改调用者自己的数据,在实际应用中需要加以区分。
(1)创建Tensor
在PyTorch中新建Tensor的方法有很多种,具体如下:
其中使用Tensor函数新建tensor是最复杂多变的方式,它既可以接收一个list,并根据list的数据新建tensor,也能根据指定的形状新建tensor,还能传入其他的tensor,下面举几个例子。
In : # 指定tensor的形状
a = t.Tensor(2,3)
a # 数值取决于内存空间的状态
Out : tensor([[1.8441e-35, 6.3619e-43, 1.8441e-35],
[6.3619e-43, 3.5071e-35, 6.3619e-43]])
In : # 用list的数据创建tensor
b = t.Tensor([[1,2,3],[4,5,6]])
b
Out : tensor([[1., 2., 3.],
[4., 5., 6.]])
In : b.tolist() # 把tensor转为list
Out : [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]]
tensor.size()返回torch.Size对象,它是tuple的子类,但其使用方式与tuple略有区别。
In : b_size = b.size()
b_size
Out : torch.Size([2, 3])
In : b.numel() # b中元素个数, 2 * 3,等价于b.nelument()
Out : 6
In : # 创建一个和b形状一样的tensor
c = t.Tensor(b_size)
# 创建一个元素为2和3的tensor
d = t.Tensor((2,3))
c,d
Out : (tensor([[1.3003e+22, 1.0723e-08, 1.3602e-05],
[2.6942e+23, 5.3835e+22, 1.0547e-08]]), tensor([2., 3.]))
除了tensor.size(),还可以利用tensor.shape直接查看tensor的形状,tensor.shape等价于tensor.size()。
In : c.shape
Out : torch.Size([2, 3])
In : c.shape??
需要注意的是,t.Tensor(*sizes)创建tensor,系统不会马上分配空间,只会计算剩余的内存是否足够使用,使用到tensor时才会分配,而其他操作都是在创建完tensor后马上进行空间分配。其他常用的创建tensor方法举例如下。
In : t.ones(2,3)
Out : tensor([[1., 1., 1.],
[1., 1., 1.]])
In : t.zeros(2,3)
Out : tensor([[0., 0., 0.],
[0., 0., 0.]])
In : t.arange(1,6,2)
Out : tensor([1, 3, 5])
In : t.linspace(1,10,3)
Out : tensor([ 1.0000, 5.5000, 10.0000])
In : t.randn(2,3)
Out : tensor([[ 1.5961, -0.3247, 0.8576],
[ 1.4467, 0.5929, 1.1375]])
In : t.randperm(5) # 长度为5的随机排列
Out : tensor([3, 0, 1, 4, 2])
In : t.eye(2,3) # 对角线为1,其他位置为0,不要求行列数一致
Out : tensor([[1., 0., 0.],
[0., 1., 0.]])
(2)常用Tensor操作
通过tensor.view方法可以调整tensor的形状,但必须保证调整前后元素总数一致。view不会修改自身的数据,返回的新tensor与源tensor共享内存,即更改其中一个,另外一个也会跟着改变。在实际应用中可能经常需要添加或减少某一维度,这时squeeze和unsqueeze两个函数就派上了用场。
In : a = t.arange(0,6)
a.view(2,3)
Out : tensor([[0, 1, 2],
[3, 4, 5]])
In : b = a.view(-1,3) # 当某一维为-1的时候,会自动计算它的大小
b
Out : tensor([[0, 1, 2],
[3, 4, 5]])
In : b.unsqueeze(1) # 注意形状,在第1维(下标从0开始)上增加“1”
Out : tensor([[[0, 1, 2]],
[[3, 4, 5]]])
In : b.unsqueeze(-2) # -2表示倒数第二个维度
Out : tensor([[[0, 1, 2]],
[[3, 4, 5]]])
In : c = b.view(1,1,1,2,3)
c.squeeze(0) # 压缩第0维的“1”
Out : tensor([[[[0, 1, 2],
[3, 4, 5]]]])
In : c.squeeze() # 把所有维度为“1”的压缩
Out : tensor([[0, 1, 2],
[3, 4, 5]])
In : a[1] = 100
b # a和b共享内存,修改了a,b也变了
Out : tensor([[ 0, 100, 2],
[ 3, 4, 5]])
resize是另一种可用来调整size的方法,但与view不同,它可以修改tensor的尺寸。如果新尺寸超过了原尺寸,会自动分配新的内存空间,而如果新尺寸小于原尺寸,则之前的数据依旧会被保存,我们来看一个例子。
In : b.resize_(1,3)
b
Out : tensor([[ 0, 100, 2]])
In : b.resize_(3,3) # 旧的数据依旧保存着,多出的数据会分配新空间
b
Out : tensor([[ 0, 100, 2],
[ 3, 4, 5],
[ 0, 0, 0]])
(3)索引操作
Tensor支持与numpy.ndarray类似的索引操作,语法上也类似,下面通过一些例子,讲解常用的索引操作。如无特殊说明,索引出来的结果与原tensor共享内存,即修改一个,另一个会跟着修改。
In : a = t.randn(3,4)
a
Out : tensor([[-0.3973, 0.0700, -0.5916, -0.4848],
[ 0.5232, 0.8094, 2.4726, 1.4351],
[-0.0845, 2.0454, -0.0363, -0.8606]])
In : a[0] # 第0行(下标从0开始)
Out : tensor([-0.3973, 0.0700, -0.5916, -0.4848])
In : a[:,0] # 第0列
Out : tensor([-0.3973, 0.5232, -0.0845])
In : a[0][2] # 第0行第2个元素,等价于a[0,2]
Out : tensor(-0.5916)
In : a[0,-1] # 第0行最后一个元素
Out : tensor(-0.4848)
In : a[:2] # 前两行
Out : tensor([[-0.3973, 0.0700, -0.5916, -0.4848],
[ 0.5232, 0.8094, 2.4726, 1.4351]])
In : a[:2,0:2] # 前两行,前两列
Out : tensor([[-0.3973, 0.0700],
[ 0.5232, 0.8094]])
In : print(a[0:1,:2]) # 第0行,前两列
print(a[0,:2]) # 注意两者的区别,形状不同
Out : tensor([[-0.3973, 0.0700]])
tensor([-0.3973, 0.0700])
In : a > 1
Out : tensor([[False, False, False, False],
[False, False, True, True],
[False, True, False, False]])
In : a[a>1] # 等价于a.maked_select(a>1),选择结果与原tensor不共享内存空间
Out : tensor([2.4726, 1.4351, 2.0454])
In : a[t.LongTensor([0,1])] # 第0行和第1行
Out : tensor([[-0.3973, 0.0700, -0.5916, -0.4848],
[ 0.5232, 0.8094, 2.4726, 1.4351]])
其他常用的选择函数如下所示。
gather是一个比较复杂的操作,对一个二维tensor,输出的每个元素如下:
out[i][j] = input[index[i][j]][j] # dim=0
out[i][j] = input[i][index[i][j]] # dim=1
三维tensor的gather操作同理,下面举几个例子。
In : a = t.arange(0,16).view(4,4)
a
Out : tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
In : # 选取对角线的元素
index = t.LongTensor([[0,1,2,3]])
a.gather(0,index)
Out : tensor([[ 0, 5, 10, 15]])
In : # 选取反对角线上的元素
index = t.LongTensor([[3,2,1,0]]).t()
a.gather(1,index)
Out : tensor([[ 3],
[ 6],
[ 9],
[12]])
In : # 选取反对角线上的元素,注意与上面的不同
index = t.LongTensor([[3,2,1,0]])
a.gather(0,index)
Out : tensor([[12, 9, 6, 3]])
In : # 选取两个对角线上的元素
index = t.LongTensor([[0,1,2,3],[3,2,1,0]]).t()
b = a.gather(1,index)
b
Out : tensor([[ 0, 3],
[ 5, 6],
[10, 9],
[15, 12]])
与gather相对应的逆操作是scatter_,gather是把数据从input中按照index取出,而scatter_是把取出的数据再放回去。注释scatter_函数是inplace操作。
out = input.gather(dim,index)
--> 近似逆操作
out = Tensor()
out.scatter_(dim,index)
# 把两个对角线元素放回到指定位置
In : c = t.zeros(4,4).long()
c.scatter_(1, index, b)
Out : tensor([[ 0, 0, 0, 3],
[ 0, 5, 6, 0],
[ 0, 9, 10, 0],
[12, 0, 0, 15]])
(4)高级索引
PyTorch 0.2版本中完善了索引操作,目前已经支持绝大多数numpy风格的高级索引。高级索引可以看成是普通索引操作的扩展,但是高级索引操作的结果一般不和原始的Tensor共享内存。
In : x = t.arange(0,27).view(3,3,3)
x
Out : tensor([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9, 10, 11],
[12, 13, 14],
[15, 16, 17]],
[[18, 19, 20],
[21, 22, 23],
[24, 25, 26]]])
In : x[[1,2],[1,2],[2,0]]
Out : tensor([14, 24])
In : x[[2,1,0],[0],[1]]
Out : tensor([19, 10, 1])
In : x[[0,2],...]
Out : tensor([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[18, 19, 20],
[21, 22, 23],
[24, 25, 26]]])
(5)Tensor类型
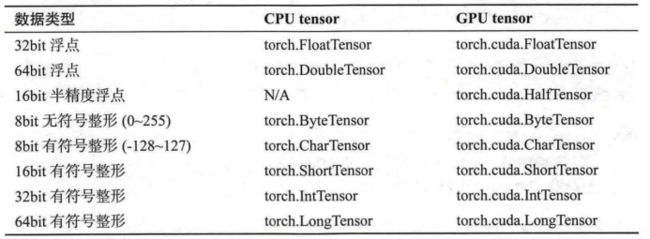
Tensor有不同的数据类型,如下表所示,每种类型分别对应有CPU和GPU版本(HalfTensor除外)。默认的Tensor是FloatTensor,可通过t.set_default_tensor_type修改默认Tensor的类型(如果默认为GPU Tensor,则所有操作都将在GPU上进行)。Tensor的类型对分析内存占用很有帮助。例如,一个size为(1000,1000,1000)的FloatTensor,它有1000 * 1000 * 1000 = 10^9个元素,每个元素占32bit/8=4Byte内存,所以共占大约4GB内存/显存。HalfTensor是专门为GPU版本设计的,同样的元素个数,显存占用只有FloatTensor的一半,所以可以极大地缓解GPU显存不足的问题,但由于HalfTensor所能表示的数值大小和精度有限,所以可能出现溢出等问题。
各数据类型之间可以互相转换,type(new_type)是通用的做法,同时还有float、long、half等快捷方法。CPU Tensor与GPU Tensor之间的相互转换通过tensor.cuda和tensor.cpu的方法实现。Tensor还有一个new方法,用法与t.Tensor一样,会调用该Tensor对应类型的构造函数,生成与当前Tensor类型一致的Tensor。
In : # 新版本PyTorch只支持FloatTensor和DoubleTensor作为默认Tensor
# 默认Tensor是FloatTensor,我们可以修改成DoubleTensor,注意参数是字符串
t.set_default_tensor_type('torch.DoubleTensor')
In : a = t.Tensor(2,3)
a # 现在a是DoubleTensor
Out : tensor([[0., 0., 0.],
[0., 0., 0.]])
In : # 把a转成IntTensor,等价于b=a.type(t.IntTensor)
b = a.int()
b
Out : tensor([[0, 0, 0],
[0, 0, 0]], dtype=torch.int32)
In : c = a.type_as(b)
c
Out : tensor([[0, 0, 0],
[0, 0, 0]], dtype=torch.int32)
In : d = a.new(2,3) # 等价于torch.Tensor(2,3)
d
Out : tensor([[0., 0., 0.],
[0., 0., 0.]])
In : # 恢复之前的默认设置
t.set_default_tensor_type('torch.FloatTensor')
(6)逐元素操作
这部分操作会对Tensor的每一个元素(point-wise,又名element-wise)进行操作,此类操作的输入和输出形状一致。常用的操作如下所示。
对于很多操作,例如div、mul、pow、fmod等,Python都实现了运算符重载,所以可以直接使用运算符。例如,a ** 2等价于torch.pow(a,2),a * 2等价于torch.mul(a,2)。
其中,clamp(x,min,max)的输出满足以下公式:
clamp常用在某些需要比较大小的地方,如取一个Tensor的每个元素与另一个数的较大值。
In : a = t.arange(0,6).view(2,3)
a
Out : tensor([[0, 1, 2],
[3, 4, 5]])
In : t.cos(a.float())
Out : tensor([[ 1.0000, 0.5403, -0.4161],
[-0.9900, -0.6536, 0.2837]])
In : a % 3 # 等价于t.fmod(a,3)
Out : tensor([[0, 1, 2],
[0, 1, 2]])
In : a ** 2 # 等价于t.pow(a,2)
Out : tensor([[ 0, 1, 4],
[ 9, 16, 25]])
In : # a中每一个元素都与3相比,取较大的一个
t.clamp(a,min=3)
Out : tensor([[3, 3, 3],
[3, 4, 5]])
(7)归并操作
此类操作会使输出形状小于输入形状,并可以沿着某一维度进行指定操作。如加法sum,既可以计算整个Tensor的和,也可以计算Tensor中 每一行或每一列的和。常用的归并操作如下所示。
以上大多数函数都有一个参数dim,用来指定这些操作是在哪个维度上执行的。关于dim(对应于Numpy中的axis)的解释众说纷纭,这里提供一个简单的记忆方式。
假设输入的形状是(m,n,k):
- 如果指定dim=0,输出的形状就是(1,n,k)或者(n,k)
- 如果指定dim=1,输出的形状就是(m,1,k)或者(m,k)
- 如果指定dim=2,输出的形状就是(m,n,1)或者(m,n)
size中是否有“1”,取决于参数keepdim,keepdim=True会保留维度1,从PyTorch 0.2版本起,keepdim默认为False。注意,以上只是经验总结,并非所有函数都符合这种形状变化方式,如cumsum。
In : b = t.ones(2,3)
b
Out : tensor([[1., 1., 1.],
[1., 1., 1.]])
In : b.sum(dim=0,keepdim=True)
Out : tensor([[2., 2., 2.]])
In : # keepdim=False,不保留维度“1”,注意形状
b.sum(dim=0,keepdim=False)
Out : tensor([2., 2., 2.])
In : b.sum(dim=1)
Out : tensor([3., 3.])
In : a = t.arange(0,6).view(2,3)
a
Out : tensor([[0, 1, 2],
[3, 4, 5]])
In : a.cumsum(dim=1) # 沿着行累加
Out : tensor([[ 0, 1, 3],
[ 3, 7, 12]])
(8)比较
比较函数中有一些是逐元素比较,操作类似于逐元素操作,还有一些则类似于归并操作。常用的比较函数如下所示。
表中第一行的比较操作已经实现了运算符重载,因此可以使用a>=b、a>b、a!=b和a==b,其返回结果是一个ByteTensor,可用来选取元素。max/min这两个操作比较特殊,以max为例,它有以下三种使用情况。
- t.max(tensor):返回Tensor中最大的一个数
- t.max(tensor,dim):指定维度上最大的数,返回Tensor和下标
- t.max(tensor1,tensor2):比较两个Tensor相比较大的元素。
In : a = t.linspace(0,15,6).view(2,3)
a
Out : tensor([[ 0., 3., 6.],
[ 9., 12., 15.]])
In : b = t.linspace(15,0,6).view(2,3)
b
Out : tensor([[15., 12., 9.],
[ 6., 3., 0.]])
In : a > b
Out : tensor([[False, False, False],
[ True, True, True]])
In : a[a>b]
Out : tensor([ 9., 12., 15.])
In : t.max(a)
Out : tensor(15.)
In : t.max(b,dim=1)
Out : torch.return_types.max(
values=tensor([15., 6.]), # 每一行的最大值
indices=tensor([0, 0])) # 对应的索引
In : t.max(a,b) # a和b对应位置比较,取出较大值构成Tensor
Out : tensor([[15., 12., 9.],
[ 9., 12., 15.]])
In : t.clamp(a,min=10) # a中每个元素和10比较,取出较大值构成Tensor
Out : tensor([[10., 10., 10.],
[10., 12., 15.]])
(9)线性代数
PyTorch的线性函数主要封装了Blas和Lapack,其用法和接口都与之类似。常用的线性代数函数如下所示。
具体使用说明请参考官方文档,需要注意的是,矩阵的转置会导致存储空间不连续,需要调用它的.contiguous方法将其转为连续。
In : b = a.t()
b.is_contiguous()
Out : False
In : b.contiguous()
Out : tensor([[ 0., 9.],
[ 3., 12.],
[ 6., 15.]])
3.1.2 Tensor和Numpy
Tensor和Numpy数组之间具有很高的相似性,彼此之间的互操作也非常简单高效,需要主要的是,Numpy和Tensor共享内存。由于Numpy历史悠久,支持丰富的操作,所以当遇到Tensor不支持的操作时,可先转成Numpy数组,处理后再转回Tensor,其转换开销很小。
- 当输入数组的某个维度的长度为1时,计算时沿此维度复制扩充成一样的形状。PyTorch当前已经支持了自动广播法则,但笔者还是建议读者通过以下两个函数的组合手动实现广播法则,这样更直观,更不易出错。
- unsqueeze或者view:为数据某一维的形状补1,实现法则1.
- expand或者expand_as,重复数组,实现法则3;该操作不会复制数组,所以不会占用额外的空间。
注意:repeat实现与expand相类似的功能,但是repeat会把相同数据复制多份,因此会占用额外的空间。
In : a = t.ones(3,2)
a
Out : tensor([[1., 1.],
[1., 1.],
[1., 1.]])
In : b = t.zeros(2,3,1)
b
Out : tensor([[[0.],
[0.],
[0.]],
[[0.],
[0.],
[0.]]])
In : # 自动广播法则
# 第一步:a是二维,b是三维,所以先在较小的a前面补1
# 即:a.unsqueeze(0),a的形状变成(1,3,2),b的形状是(2,3,1)
# 第二步:a和b在第一维和第三维的形状不一样,其中一个为1
# 可以利用广播法则扩展,两个形状都变成了(2,3,2)
a + b
Out : tensor([[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]]])
In : # 手动广播法则
# 或者a.view(1,3,2).expand(2,3,2)+b.expand(2,3,2)
a.unsqueeze(0).expand(2,3,2)+b.expand(2,3,2)
Out : tensor([[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]]])
In : a = np.ones([2,3],dtype=np.float32)
a
Out : array([[1., 1., 1.],
[1., 1., 1.]], dtype=float32)
In : b = t.from_numpy(a)
b
Out : tensor([[1., 1., 1.],
[1., 1., 1.]])
In : c = b.numpy() # a,b,c三个对象共享内存
c
Out : array([[1., 1., 1.],
[1., 1., 1.]], dtype=float32)
In : # 也可以直接将Numpy对象传入Tensor,这种情况下若Numpy类型不是Float32会新建,不会共享内存
d = np.ones([2,3],dtype=np.int)
e = t.Tensor(d)
d[0,1]=100
e
Out : tensor([[1., 1., 1.],
[1., 1., 1.]])
广播法则(Broadcast)是科学运算中经常使用的一个技巧,它在快速执行向量化的同时不会占用额外的内存或显存。Numpy的广播法则定义如下:
- 让所有输入数组都向其中shape最长的数组看齐,shape中不足的部分通过再前面加1补齐。
- 两个数组要么在某一个维度的长度一致,要么其中一个为1,否则不计算。
In : # expand不会占用额外空间,只会在需要时才扩充,可极大地节省内存
e = a.unsqueeze(0).expand(10000000000000,3,2)
3.1.3 内部结构
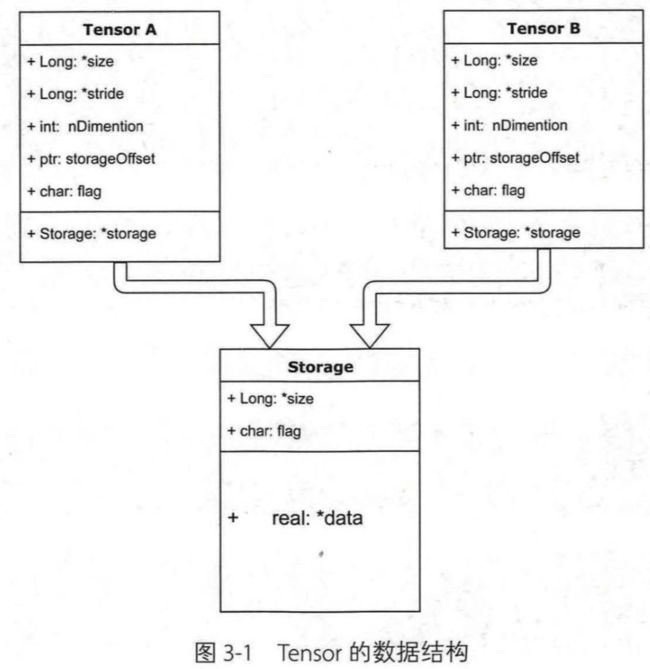
Tensor的数据结构如下图所示。Tensor分为头信息区(Tensor)和存储区(Storage),信息区主要保存着Tensor的形状(size)、步长(stride)、数据类型(type)等信息,而真正的数据则保存成连续数组。由于数据动辄成千上万,因此信息区元素占用内存较少,主要内存占用取决于Tensor中元素的数目,即存储区的大小。
一般来说,一个Tensor有着与之对应的Storage,Storage是在Data之上封装的接口,便于使用。不同Tensor的头信息一般不同,但却可能使用相同的Storage。下面我们来看两个例子。
In : a = t.arange(0,6).float()
a.storage()
Out : 0.0
1.0
2.0
3.0
4.0
5.0
[torch.FloatStorage of size 6]
In : b = a.view(2,3)
b.storage()
Out : 0.0
1.0
2.0
3.0
4.0
5.0
[torch.FloatStorage of size 6]
In : # 一个对象的id值可以看作它在内存中的地址
# a和b的storage的内存地址一样,即是同一个storage
id(b.storage())==id(a.storage())
Out : True
In : # a改变,b也随之改变,因为它们是共享storage
a[1] = 100
b
Out : tensor([[ 0., 100., 2.],
[ 3., 4., 5.]])
In : c = a[2:]
c.storage()
Out : 0.0
100.0
2.0
3.0
4.0
5.0
[torch.FloatStorage of size 6]
In : c.data_ptr(),a.data_ptr() # data_ptr返回Tensor首元素的内存地址
# 可以看出相差8,这是因为2 * 4 = 8相差两个元素,每个Float型元素占4个字节
Out : (2615363991816, 2615363991808)
In : c[0] = -100 # c[0]的内存地址对应a[2]的内存地址
a
Out : tensor([ 0., 100., -100., 3., 4., 5.])
In : d = t.Tensor(c.storage())
d[0] = 6666
b
Out : tensor([[ 6.6660e+03, 1.0000e+02, -1.0000e+02],
[ 3.0000e+00, 4.0000e+00, 5.0000e+00]])
In : # 下面四个Tensor共享内存
id(a.storage()) == id(b.storage()) == id(c.storage()) == id(d.storage())
Out : True
In : a.storage_offset(), c.storage_offset(), d.storage_offset()
Out : (0, 2, 0)
In : e = b[::2,::2] # 隔2行,隔2列取一个元素
id(e.storage()) == id(a.storage())
Out : True
In : b.stride(),e.stride()
Out : ((3, 1), (6, 2))
In : e.is_contiguous()
Out : False
可见绝大多数操作并不修改Tensor的数据,只是修改了Tensor的头信息。这种做法更节省内存,同时提升了处理速度。此外,有些操作会导致Tensor不连续,这是需要调用tensor.contiguous方法将它们变成连续的数据,该方法复制数据到新的内存,不再与原来的数据共享storage。另外,读者可以思考一下,之前说过的高级索引一般不共享storage,而普通索引共享storage,这是为什么呢?(提示:普通索引可以通过修改tensor的offset、stride和size实现,不修改storage的数据,高级索引不行)。
3.1.4 其他有关Tensor的话题
这部分的内存不好专门划分为一节,但笔者认为值得读者注意,故将其放在本节。
(1)持久化
Tensor的保存和加载十分简单,使用t.save和t.load即可完成相应的功能。在save/load时可指定使用的pickle模块,在load时还可将GPU tensor映射到CPU或其他GPU上。
In : if t.cuda.is_available():
a = a.cuda(0) # 把a转为GPU-0上的Tensor
t.save(a,'a.pth')
# 加载为b,储存于GPU-0上(因为保存时tensor就在GPU-1上)
b = t.load('a.pth')
# 加载为c,存储于CPU
c = t.load('a.pth',map_location=lambda storage,loc: storage)
# 加载维d,存储于GPU-0上
d = t.load('a.pth',map_location={'cuda:1':'cuda:0'})
(2)向量化
向量化计算是一种特殊的并行计算方式,一般程序在同一时间只执行一个操作的方式,它可在同一时间执行多个操作,通常是对不同的数据执行同样的一个或一批命令,或者说把指令应用于一个数组或向量上。向量化可极大地提高科学运算的效率,Python本身是一门高级语言,使用很方便,但许多操作很低效,尤其是for循环。在科学计算程序中应当极力避免使用Python原生的for循环,尽量使用向量化的数值计算。
In : def for_loop_add(x,y):
result = []
for i,j in zip(x,y):
result.append(i+j)
return t.Tensor(result)
In : x = t.zeros(100)
y = t.ones(100)
%timeit -n 10 for_loop_add(x,y)
%timeit -n 10 x + y
Out : 744 µs ± 60.2 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
The slowest run took 8.83 times longer than the fastest. This could mean that an intermediate result is being cached.
6.42 µs ± 6.71 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
可见二者有超过10倍的速度差距,因此在实际应用中应尽量调用内建函数(buildin-function),这些函数底层由C/C++实现,能通过执行底层优化实现高效计算。因此在平时写代码时,就应养成向量化的思维习惯。
此外,还有以下几点需要注意:
- 大多数t.function都有一个参数out,这时产生的结果将保存在out指定的tensor之中。
- t.set_num_threads可以设置PyTorch进行CPU多线程并行计算时所占用的线程数,用来限制PyTorch所占用的PCU数目。
- t.set_printoptions可以用来设置打印tensor时的数值精度和格式。下面举例说明。
In : a = t.arange(2**31,2**31+10).int()
print(a[-1],a[-2]) # 32bit的IntTensor精度有限导致溢出
b = t.LongTensor()
t.arange(2**31,2**31+10,out=b) # 64bit的LongTensor不会溢出
print(b[-1],b[-2])
Out : tensor(-2147483639, dtype=torch.int32) tensor(-2147483640, dtype=torch.int32)
tensor(2147483657) tensor(2147483656)
In : a = t.randn(2,3)
a
Out : tensor([[-0.6321, 0.7025, -0.0330],
[ 0.1462, 0.7813, -0.7753]])
In : t.set_printoptions(precision=10)
a
Out : tensor([[-0.6321436763, 0.7024819851, -0.0329958275],
[ 0.1461933255, 0.7812925577, -0.7752825022]])
3.1.5 小试牛刀:线性回归
线性回归是机器学习的入门知识,应用十分广泛。线性回归利用数理统计中的回归来确定两种或两种以上变量间的相互依赖的定量关系,其表达形式为,误差服从均值为0的正态分布。线性回归的损失函数是:
利用随机梯度下降法更新参数和来最小化损失函数,最终学得和的数值。
import torch as t
%matplotlib inline
from matplotlib import pyplot as plt
from IPython import display
device = t.device('cpu') #如果你想用gpu,改成t.device('cuda:0')
# 设置随机数种子,保证在不同电脑上运行时下面的输出一致
t.manual_seed(1000)
def get_fake_data(batch_size=8):
''' 产生随机数据:y=x*2+3,加上了一些噪声'''
x = t.rand(batch_size, 1, device=device) * 20
y = x * 2 + 3 + t.randn(batch_size, 1, device=device)
return x, y
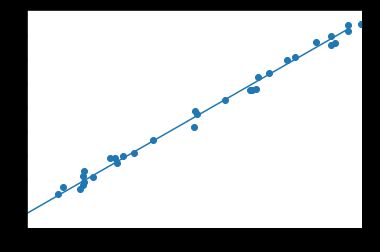
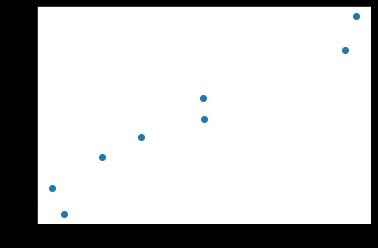
# 来看看产生的x-y分布
x, y = get_fake_data(batch_size=16)
plt.scatter(x.squeeze().cpu().numpy(), y.squeeze().cpu().numpy())
输出如下:
# 随机初始化参数
w = t.rand(1, 1).to(device)
b = t.zeros(1, 1).to(device)
lr =0.001 # 学习率
for ii in range(20000):
x, y = get_fake_data()
# forward:计算loss
y_pred = x * w + b
loss = 0.5 * (y_pred - y) ** 2 # 均方误差
loss = loss.mean()
# backward:手动计算梯度
dloss = 1
dy_pred = dloss * (y_pred - y)
dw = x.t().mm(dy_pred)
db = dy_pred.sum()
# 更新参数
w.sub_(lr * dw)
b.sub_(lr * db)
if ii % 1000 == 0:
# 画图
display.clear_output(wait=True)
x = t.arange(0, 20).view(-1, 1).float()
y = x * w + b
plt.plot(x.cpu().numpy(), y.cpu().numpy()) # predicted
x2, y2 = get_fake_data(batch_size=32)
plt.scatter(x2.numpy(), y2.numpy()) # true data
plt.xlim(0,20)
plt.ylim(0,45)
plt.show()
plt.pause(0.5)
print('w = ',w.item())
print('b = ',b.item())
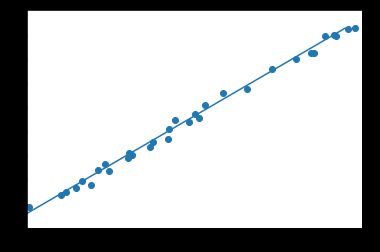
输出如下:
w = 2.0093319416046143
b = 3.007240056991577
可见程序已经基本学出w=2、b=3,并且图中直线和数据已经实现较好的拟合。
虽然上面提到了许多操作,但是只要掌握了这个例子基本上就可以了,其他的知识,读者日后遇到的时候,可以再看看这部份的内容或者查找对应文档。
3.2 autograd
用Tensor训练网络很方便,但从3.1节最后的线性回归例子来看,反向传播过程需要手动实现。这对线性回归这种较简单的模型来说还比较容易,但实际使用中经常出现非常复杂的网络结构,此时如果手动实现反向传播,不仅费时费力,而且容易出错,难以检查。torch.autograd就是为了方便用户使用,专门开发的一套自动求导引擎,它能够根据输入和前向传播过程自动构建计算图,并执行反向传播。
计算图(Computation Graph)是现代深度学习框架(如PyTorch和TensorFlow等)的核心,它为自动求导算法——反向传播(Back Propogation)提供了理论支持,了解计算图在实际写程序过程中会有极大帮助。本节会涉及一些基础的计算图知识,但并不要求读者事先对此有深入了解。关于计算图的基础知识推荐阅读Christopher Olah的文章《Calculus on Computational Graphs: Backpropagation》。
3.2.1 Variable
PyTorch在autograd模块中实现了计算图的相关功能,autograd中的核心数据结构是Variable。Variable封装了tensor,并记录对tensor的操作记录用来构建计算图。Variable的数据结构如下图所示,主要包括三个属性。
- data:保存variable所包含的tensor。
- grad:保存data对应的梯度,grad也是variable,而非tensor,它与data形状一致。
- grad_fn:指向一个Function,记录variable的操作历史,即它是什么操作的输出,用来构建计算图。如果某一个变量是由用户创建的,则它为叶子节点,对应的grad_fn等于None。
Variable的构造函数需要出入tensor,同时有两个可选参数。
- requires_grad(bool):是否需要对该variable进行求导。
- volatile(bool):意为“挥发”,设置为True,构建在该variable之上的图都不会求导,专为推理阶段设计。
Variable支持大部分tensor支持的函数,但其不支持部分inplace函数,因为这些函数会修改tensor自身,而在反向传播中,variable需要缓存原来的tensor来计算梯度。如果想要计算各个Variable的梯度,只需调用根节点variable的backward方法,autograd会自动沿着计算图反向传播,计算每一个叶子节点的梯度。
variable.backward(grad_variables=None,retain_graph=None,create_graph=None)主要有如下参数。
- grad_variables:形状与variable一致,对于y.backward(),grad_variables相当于链式法则中的。grad_variables也可以是tensor或序列。
- retain_graph:反向传播需要缓存一些中间结果,反向传播之后,这些缓存就被清空,可通过指定这个参数不清空缓存,用来多次反向传播。
- create_graph:对反向传播过程再次构建计算图,可通过backward of backward实现求高阶导数。
上述描述可能比较抽象,如果没有看懂也不用着急,笔者会在本节后半部分详细介绍,下面先看几个例子。
In : from __future__ import print_function
import torch
from torch.autograd import Variable
In : # 从tensor中创建variable,指定需要求导
a = Variable(torch.ones(3,4),requires_grad=True)
a
Out : tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]], requires_grad=True)
In : b = Variable(torch.zeros(3,4))
b
Out : tensor([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
In : # 函数的使用与tensor一致,也可写成c = a + b
c = a.add(b)
c
Out : tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]], grad_fn=)
In : d = c.sum()
d.backward() # 反向传播
In : # 注意二者的区别
# 前者在取data后变为tensor,从tensor计算sum得到float
# 后者计算sum后仍然是Variable
c.data.sum(),c.sum()
Out : (tensor(12.), tensor(12., grad_fn=))
In : a.grad
Out : tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
In : # 此处虽然没有指定c需要求导,但c依赖于a,而a需要求导
# 因此c的requires_grad属性会自动设为True
a.requires_grad,b.requires_grad,c.requires_grad
Out : (True, False, True)
In : # 由用户创建的variable属性叶子节点,对应的grad_fn是None
a.is_leaf,b.is_leaf,c.is_leaf
Out : (True, True, False)
In : # c.grad是None,c不是叶子节点,它的梯度是用来计算a的梯度
# 虽然c.requires_grad = True,但其梯度计算完之后即被释放
c.grad is None
Out : True
接着我们来看看autograd计算的导数和我们手动推导的导数的区别。
它的导函数是:
In : def f(x):
'''计算y'''
y = x ** 2 * torch.exp(x)
return y
def gradf(x):
'''手动求导函数'''
dx = 2 * x * torch.exp(x) + x ** 2 * torch.exp(x)
return dx
In : x = Variable(torch.randn(3,4),requires_grad=True)
y = f(x)
y
Out : tensor([[1.8043e-04, 1.7765e-03, 1.1095e-01, 1.2061e-01],
[2.2261e+01, 4.6146e-01, 1.6656e-01, 2.5974e-01],
[1.7301e-01, 7.1263e-02, 4.5603e-05, 3.2861e-01]],
grad_fn=)
In : y.backward(torch.ones(y.size())) # grad_variables形状与y一致
x.grad
Out : tensor([[-2.6503e-02, 8.7831e-02, -4.3213e-01, -4.3939e-01],
[ 4.6188e+01, -2.4654e-01, -4.5883e-01, -4.4553e-01],
[-4.5991e-01, 6.7237e-01, 1.3597e-02, -4.0307e-01]])
In : # autograd的计算结果与利用公式手动计算的结果一致
gradf(x)
Out : tensor([[-2.6503e-02, 8.7831e-02, -4.3213e-01, -4.3939e-01],
[ 4.6188e+01, -2.4654e-01, -4.5883e-01, -4.4553e-01],
[-4.5991e-01, 6.7237e-01, 1.3597e-02, -4.0307e-01]],
grad_fn=)
3.2.2 计算图
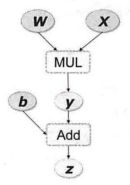
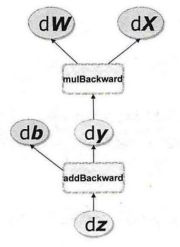
PyTorch中autograd的底层才用了计算图,计算图是一种特殊的有向无环图(DAG),用于记录算子与变量之间的关系。一般用矩形表示算子,椭圆形表示变量。如表达式可分解为和,其计算图如下所示。图中MUL和ADD都是算子,、、为变量。
如果有向无环图中,和是叶子结点(leaf node),这些节点通常由用户自己创建,不依赖于其他变量。称为根节点,是计算图的最终目标。利用链式法则很容易求得各个叶子节点的梯度。
而有了计算图,上述链式求导即可利用计算图的反向传播自动完成,其过程如下图所示。
在PyTorch实现中,autograd会随着用户的操作,记录生成当前variable的所有操作,并由此建立一个有向无环图。用户每进行一个操作,相应的计算图就会发生改变。更底层的实现中,图中记录了操作Function,每一个变量在图中的位置可通过其grad_fn属性在图中的位置推测得到。在反向传播过程中,autograd沿着这个图从当前变量(根节点)溯源,可以利用链式求导法则计算所有叶子节点的梯度。每一个前向传播操作的函数都有与之对应的反向传播函数用来计算输入的各个variable的梯度,这些函数的函数名通常以Backward结尾。下面结合代码学习autograd的实现细节。
In : x = Variable(torch.ones(1))
b = Variable(torch.rand(1),requires_grad=True)
w = Variable(torch.rand(1),requires_grad=True)
y = w * x # 等价于 y = w.mul(x)
z = y + b # 等价于 z = y.add(b)
In : x.requires_grad,b.requires_grad,w.requires_grad
Out : (False, True, True)
In : # 虽然未指定y.requires_grad为True,但由于y依赖于需要求导的w
# 故而y.requires_grad为True
y.requires_grad
Out : True
In : x.is_leaf,w.is_leaf,b.is_leaf
Out : (True, True, True)
In : y.is_leaf,z.is_leaf
Out : (False, False)
In : # grad_fn可以查看这个variable的反向传播函数
# z是add函数的输出,所以它的反向传播函数是AddBackward
z.grad_fn
Out :
In : # next_functions保存grad_fn的输入,grad_fn的输入是一个tuple
# 第一个是y,它是乘法(mul)的输出,所以对应的反向传播函数y.grad_fn是MulBackward
# 第二个是b,它是叶子节点,由用户创建,grad_fn为None,但是有
z.grad_fn.next_functions
Out : ((, 0), (, 0))
In : # variable的grad_fn对应着图中的function
z.grad_fn.next_functions[0][0] == y.grad_fn
Out : True
In : # 第一个是w,叶子节点,需要求导,梯度是累加的
# 第二个是x,叶子节点,不需要求导,所以为None
y.grad_fn.next_functions
Out : ((, 0), (None, 0))
In : # 叶子节点的grad_fn是None
w.grad_fn,x.grad_fn
Out : (None, None)
计算的梯度时需要用到的数值(),这些数值在前向过程中会保存成buffer,在计算完梯度之后会自动清空。为了能够多次反向传播需要指定retain_graph来保留这些buffer。
In : # 使用retain_graph保存buffer
z.backward(retain_graph=True)
w.grad
Out : tensor([1.])
In : # 多次反向传播,梯度累加,这也就是w中AccumulateGrad标识的含义
z.backward()
w.grad
Out : tensor([2.])
PyTorch使用的是动态图,它的计算图在每次前向传播时都是从头开始构建的,所以它能够使用Python控制语句(如for、if等),根据需求创建计算图。这一点在自然语言处理领域中很有用,它意味着你不需要事先构建所有可能用到的图的路径,图在运行时才构建。
In : def abs(x):
if x.data[0]>0:
return x
else:
return -x
In : x = Variable(torch.ones(1),requires_grad=True)
y = abs(x)
y.backward()
x.grad
Out : tensor([1.])
In : x = Variable(-1 * torch.ones(1),requires_grad=True)
y = abs(x)
y.backward()
x.grad
Out : tensor([-1.])
In : def f(x):
result = 1
for ii in x:
if ii > 0:
result = ii * result
return result
In : x = Variable(torch.arange(-2,4).float(),requires_grad=True)
y = f(x) # y = x[3] * x[4] * x[5]
y.backward()
x.grad
Out : tensor([0., 0., 0., 6., 3., 2.])
变量的requires_grad属性默认为False,如果某一个节点requires_grad被设置为True,那么所有依赖它的节点requires_grad都是True。这其实很好理解,对于 x→y→z ,x.requires_grad = True,当需要计算时,根据链式法则,,自然也需要求,所以y.requires_grad会被自动标为True.
有些时候我们可能不希望autograd对tensor求导。因为求导需要缓存许多中间结果,增加额外的内存/显存开销,那么我们可以关闭自动求导。对于不需要反向传播的情景(如inference,即测试推理时),关闭自动求导可实现一定程度的速度提升,并节省约一半显存,因其不需要分配空间计算梯度。
In : x = torch.ones(1)
w = torch.rand(1,requires_grad=True)
y = x * w
# y依赖于w,而w.requires_grad=True
x.requires_grad,w.requires_grad,y.requires_grad
Out : (False, True, True)
In : with torch.no_grad():
x = torch.ones(1)
w = torch.rand(1, requires_grad = True)
y = x * w
# y依赖于w和x,虽然w.requires_grad = True,但是y的requires_grad依旧为False
x.requires_grad, w.requires_grad, y.requires_grad
Out : (False, True, False)
In : torch.set_grad_enabled(False)
x = torch.ones(1)
w = torch.rand(1, requires_grad = True)
y = x * w
# y依赖于w和x,虽然w.requires_grad = True,但是y的requires_grad依旧为False
x.requires_grad, w.requires_grad, y.requires_grad
Out : (False, True, False)
In : # 恢复默认配置
torch.set_grad_enabled(True)
Out :
如果我们想要修改tensor的数值,但是又不希望被autograd记录,那么我么可以对tensor.data进行操作。
In : a = torch.ones(3,4,requires_grad=True)
b = torch.ones(3,4,requires_grad=True)
c = a * b
a.data # 还是一个tensor
Out : tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
In : a.data.requires_grad # 但是已经是独立于计算图之外
Out : False
In : d = a.data.sigmoid_() # sigmoid_ 是个inplace操作,会修改a自身的值
d.requires_grad
Out : False
In : a
Out : tensor([[0.7311, 0.7311, 0.7311, 0.7311],
[0.7311, 0.7311, 0.7311, 0.7311],
[0.7311, 0.7311, 0.7311, 0.7311]], requires_grad=True)
如果我们希望对tensor,但是又不希望被记录, 可以使用tensor.data 或者tensor.detach()。
In : a.requires_grad
Out : True
In : # 近似于 tensor=a.data, 但是如果tensor被修改,backward可能会报错
tensor = a.detach()
tensor.requires_grad
Out : False
In : # 统计tensor的一些指标,不希望被记录
mean = tensor.mean()
std = tensor.std()
maximum = tensor.max()
In : tensor[0]=1
# 下面会报错: RuntimeError: one of the variables needed for gradient
# computation has been modified by an inplace operation
# 因为 c=a*b, b的梯度取决于a,现在修改了tensor,其实也就是修改了a,梯度不再准确
# c.sum().backward()
在反向传播过程中,非叶子节点的导数计算完之后即被清空。若想查看这些变量的梯度,有以下两种方法。
- 使用autograd.grad方法
- 使用hook方法
autograd.grad和hook方法都是很强大的工具,更详细的用法参考官方API文档,这里只举例说明其基础的使用方法。推荐使用hook方法,但是在实际使用中应尽量避免修改grad的值。
In : x = torch.ones(3, requires_grad=True)
w = torch.rand(3, requires_grad=True)
y = x * w
# y依赖于w,而w.requires_grad = True
z = y.sum()
x.requires_grad, w.requires_grad, y.requires_grad
Out : (True, True, True)
In : # 非叶子节点grad计算完之后自动清空,y.grad是None
z.backward()
(x.grad, w.grad, y.grad)
Out : (tensor([0.0910, 0.6889, 0.9226]), tensor([1., 1., 1.]), None)
In : # 第一种方法:使用grad获取中间变量的梯度
x = torch.ones(3, requires_grad=True)
w = torch.rand(3, requires_grad=True)
y = x * w
z = y.sum()
# z对y的梯度,隐式调用backward()
torch.autograd.grad(z, y)
Out : (tensor([1., 1., 1.]),)
In : # 第二种方法:使用hook
# hook是一个函数,输入是梯度,不应该有返回值
def variable_hook(grad):
print('y的梯度:',grad)
x = torch.ones(3, requires_grad=True)
w = torch.rand(3, requires_grad=True)
y = x * w
# 注册hook
hook_handle = y.register_hook(variable_hook)
z = y.sum()
z.backward()
# 除非你每次都要用hook,否则用完之后记得移除hook
hook_handle.remove()
Out : y的梯度: tensor([1., 1., 1.])
最后再来看看variable中grad属性和backward函数grad_variables参数的含义:
- 的梯度是目标函数对的梯度,,形状和一致。
- 对于y.backward(grad_variables)中的grad_variables相当于链式求导法则中的中的。是目标函数,一般是一个标量,故而 的形状与的形状一致。z.backward()在一定程度上等价于y.backward(grad_y)。z.backward()省略了grad_variables参数,是因为是一个标量,而。
In : x = torch.arange(0,3, requires_grad=True, dtype=torch.float32)
y = x**2 + x*2
z = y.sum()
z.backward() # 从z开始反向传播
x.grad
Out : tensor([2., 4., 6.])
In : x = torch.arange(0,3, requires_grad=True, dtype=torch.float32)
y = x**2 + x*2
z = y.sum()
y_gradient = torch.Tensor([1,1,1]) # dz/dy
y.backward(y_gradient) #从y开始反向传播
x.grad
Out : tensor([2., 4., 6.])
另外值得注意的是,只有对variable的操作才能使用autograd,如果对variable的data直接进行操作,将无法使用反向传播。除了对参数初始化,一般我们不会修改variable.data的值。
在PyTorch中计算图的特点可总结如下:
- autograd根据用户对variable的操作构建其计算图。对变量的操作抽象为Function。
- 对于那些不是任何函数(Function)的输出,由用户创建的节点称为叶子节点,叶子节点的grad_fn为None。叶子节点中需要求导的variable,具有AccumulateGrad标识,因其梯度是累加的。
- variable默认是不需要求导的,即requires_grad属性默认为False,如果某一个节点requires_grad被设置为True,那么所有依赖它的节点requires_grad都为True。
- variable的volatile属性已经废除了。
- 多次反向传播时,梯度是累加的。反向传播的中间缓存会被清空,为进行多次反向传播需指定retain_graph=True来保存这些缓存。
- 非叶子节点的梯度计算完之后即被清空,可以使用autograd.grad或hook技术获取非叶子节点的值。
- variable的grad与data形状一致,应避免直接修改variable.data,因为对data的直接操作无法利用autograd进行反向传播。
- 反向传播函数backward的参数grad_variables可以看成链式求导的中间结果,如果是标量,可以省略,默认为1。
- PyTorch采用动态图设计,可以很方便地查看中间层的输出,动态的设计计算图结构。
这些知识不懂大多数情况下也不会影响对PyTorch的使用,但是掌握这些知识有助于更好地理解PyTorch,并有效的避开很多陷阱。
3.2.3 扩展autograd
目前,绝大多数函数都可以使用autograd实现反向求导,但如果需要自己写一个复杂的函数,不支持自动反向求导怎么办? 答案是写一个Function,实现它的前向传播和反向传播代码,Function对应于计算图中的矩形,它接收参数,计算并返回结果。下面给出一个例子。
In : from torch.autograd import Function
class Mul(Function):
@staticmethod
def forward(ctx, w, x, b, x_requires_grad = True):
ctx.x_requires_grad = x_requires_grad
ctx.save_for_backward(w,x)
output = w * x + b
return output
@staticmethod
def backward(ctx, grad_output):
w,x = ctx.saved_tensors
grad_w = grad_output * x
if ctx.x_requires_grad:
grad_x = grad_output * w
else:
grad_x = None
grad_b = grad_output * 1
return grad_w, grad_x, grad_b, None
对以上代码的分析如下:
- 自定义的Function需要继承autograd.Function,没有构造函数init,forward和backward函数都是静态方法。
- forward函数的输入和输出都是tensor,backward函数的输入和输出都是variable。
- backward函数的输出和forward函数的输入对应,backward函数的输入和forward函数的输出对应。
- backward函数的grad_output参数即torch.autograd.backward中的grad_variables。
- 如果某一个输入不需要求导,直接返回None,如forward中的输入参数x_requires_grad显然无法对它求导,直接返回None即可。
- 反向传播可能需要利用前向传播的某些中间结果,在前向传播过程中,需要保存中间结果,否则前向传播结束后这些对象即被释放。
使用Function.apply(variable)即可调用实现的Function。
In : from torch.autograd import Function
class MultiplyAdd(Function):
@staticmethod
def forward(ctx, w, x, b):
ctx.save_for_backward(w,x)
output = w * x + b
return output
@staticmethod
def backward(ctx, grad_output):
w,x = ctx.saved_tensors
grad_w = grad_output * x
grad_x = grad_output * w
grad_b = grad_output * 1
return grad_w, grad_x, grad_b
In : x = torch.ones(1)
w = torch.rand(1, requires_grad = True)
b = torch.rand(1, requires_grad = True)
# 开始前向传播
z=MultiplyAdd.apply(w, x, b)
# 开始反向传播
z.backward()
# x不需要求导,中间过程还是会计算它的导数,但随后被清空
x.grad, w.grad, b.grad
Out : (None, tensor([1.]), tensor([1.]))
In : x = torch.ones(1)
w = torch.rand(1, requires_grad = True)
b = torch.rand(1, requires_grad = True)
#print('开始前向传播')
z=MultiplyAdd.apply(w,x,b)
#print('开始反向传播')
# 调用MultiplyAdd.backward
# 输出grad_w, grad_x, grad_b
z.grad_fn.apply(torch.ones(1))
Out : (tensor([1.]), tensor([0.7181], grad_fn=), tensor([1.]))
之所以forward函数的输入是tensor,而backward函数的输入是variable,这是为了实现高阶求导。backward函数的输入输出虽然是variable,但在实际使用时autograd.Function会将输入variable提取为tensor,并将计算结果的tensor封装成variable返回。在backward函数中,之所以也要对variable进行操作,是为了能够计算梯度的梯度(backward of backward)。下面举例说明,有关torch.autograd.grad的更详细使用请参照文档。
In : x = torch.tensor([5], requires_grad=True, dtype=torch.float32)
y = x ** 2
grad_x = torch.autograd.grad(y, x, create_graph=True)
grad_x # dy/dx = 2 * x
Out : (tensor([10.], grad_fn=),)
In : grad_grad_x = torch.autograd.grad(grad_x[0],x)
grad_grad_x # 二阶导数 d(2x)/dx = 2
Out : (tensor([2.]),)
这种设计虽然能让autograd具有高阶求导功能,但其也限制了Tensor的使用,因autograd中反向传播的函数只能利用当前已经有的Variable操作。为了更好的灵活性,也为了兼容旧版本的代码,PyTorch还提供了另外一种扩展autograd的方法。PyTorch提供了一个装饰器@once_differentiable,能够在backward函数中自动将输入的variable提取成tensor,把计算结果的tensor自动封装成variable。有了这个特性我们就能够很方便的使用numpy/scipy中的函数,操作不再局限于variable所支持的操作。但是这种做法正如名字中所暗示的那样只能求导一次,它打断了反向传播图,不再支持高阶求导。
上面所描述的都是新式Function,还有个legacy Function,可以带有init方法,forward和backwad函数也不需要声明为@staticmethod,但随着版本更迭,此类Function将越来越少遇到,在此不做更多介绍。
此外在实现了自己的Function之后,还可以使用gradcheck函数来检测实现是否正确。gradcheck通过数值逼近来计算梯度,可能具有一定的误差,通过控制eps的大小可以控制容忍的误差。关于这部份的内容可以参考github上开发者们的讨论。
下面举例说明如何利用Function实现sigmoid Function。
In : class Sigmoid(Function):
@staticmethod
def forward(ctx, x):
output = 1 / (1 + torch.exp(-x))
ctx.save_for_backward(output)
return output
@staticmethod
def backward(ctx, grad_output):
output, = ctx.saved_tensors
grad_x = output * (1 - output) * grad_output
return grad_x
In : # 采用数值逼近方式检验计算梯度的公式对不对
test_input = torch.randn(3,4, requires_grad=True)
torch.autograd.gradcheck(Sigmoid.apply, (test_input,), eps=1e-3)
Out : True
In : def f_sigmoid(x):
y = Sigmoid.apply(x)
y.backward(torch.ones(x.size()))
def f_naive(x):
y = 1/(1 + torch.exp(-x))
y.backward(torch.ones(x.size()))
def f_th(x):
y = torch.sigmoid(x)
y.backward(torch.ones(x.size()))
In : x=torch.randn(100, 100, requires_grad=True)
%timeit -n 100 f_sigmoid(x)
%timeit -n 100 f_naive(x)
%timeit -n 100 f_th(x)
Out : 232 µs ± 123 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
211 µs ± 48.2 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
The slowest run took 4.32 times longer than the fastest. This could mean that an intermediate result is being cached.
195 µs ± 149 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
显然f_sigmoid要比单纯利用autograd加减和乘方操作实现的函数快不少,因为f_sigmoid的backward优化了反向传播的过程。另外可以看出系统实现的built-in接口(t.sigmoid)更快。
3.2.4 小试牛刀:用Variable实现线性回归
在上一节中讲解了利用tensor实现线性回归,在这一小节中,将讲解如何利用autograd/Variable实现线性回归,以此感受autograd的便捷之处。
import torch as t
%matplotlib inline
from matplotlib import pyplot as plt
from IPython import display
import numpy as np
# 设置随机数种子,为了在不同人电脑上运行时下面的输出一致
t.manual_seed(1000)
def get_fake_data(batch_size=8):
''' 产生随机数据:y = x*2 + 3,加上了一些噪声'''
x = t.rand(batch_size,1) * 20
y = x * 2 + 3 + t.randn(batch_size, 1)
return x, y
# 来看看产生x-y分布是什么样的
x, y = get_fake_data()
plt.scatter(x.squeeze().numpy(), y.squeeze().numpy())
输出如下:
# 随机初始化参数
w = t.rand(1,1, requires_grad=True)
b = t.zeros(1,1, requires_grad=True)
losses = np.zeros(20000)
lr =0.001 # 学习率
for ii in range(20000):
x, y = get_fake_data()
# forward:计算loss
y_pred = x.mm(w) + b.expand_as(y)
loss = 0.5 * (y_pred - y) ** 2
loss = loss.sum()
losses[ii] = loss.item()
# backward:手动计算梯度
loss.backward()
# 更新参数
w.data.sub_(lr * w.grad.data)
b.data.sub_(lr * b.grad.data)
# 梯度清零
w.grad.data.zero_()
b.grad.data.zero_()
if ii%1000 ==0:
# 画图
display.clear_output(wait=True)
x = t.arange(0, 20).view(-1, 1).float()
y = x.mm(w.data) + b.data.expand_as(x)
plt.plot(x.numpy(), y.numpy()) # predicted
x2, y2 = get_fake_data(batch_size=32)
plt.scatter(x2.numpy(), y2.numpy()) # true data
plt.xlim(0,20)
plt.ylim(0,45)
plt.show()
plt.pause(0.5)
print('w = ',w.item())
print('b = ',b.item())
输出如下:
w = 1.996268630027771
b = 3.0148122310638428
用autograd实现的线性回归最大的不同点就在于autograd不需要计算反向传播,可以自动计算微分。这点不单是在深度学习,在许多机器学习的问题中都很有用。另外需要注意的是在每次反向传播之前要记得先把梯度清零。
本章主要介绍了PyTorch中两个基础底层的数据结构:Tensor和autograd中的Variable。Tensor是一个类似Numpy数组的高效多维数值运算数据结构,有着和Numpy相类似的接口,并提供简单易用的GPU加速。Variable是autograd封装了Tensor并提供自动求导技术的,具有和Tensor几乎一样的接口。autograd是PyTorch的自动微分引擎,采用动态计算图技术,能够快速高效的计算导数。