树
在n个结点的树中有n-1条边。
树中一个结点的子结点个数称为该结点的度,树中结点的最大度数称为树的度。
有序树和无序树(左右子树是否有顺序)
路径只能从上到下,同一双亲结点的两个孩子结点之间不存在路径。
树的性质
1.结点数等于所有结点的度数加1
2.度为m的树中第i层上至多有m^(i-1)个结点
3.高度h的m叉树至多有(m^h-1)/(m-1)个结点
4.具有n个结点的m叉树的最小高度为:向上取整(log(m)(n(m-1)+1))
二叉树
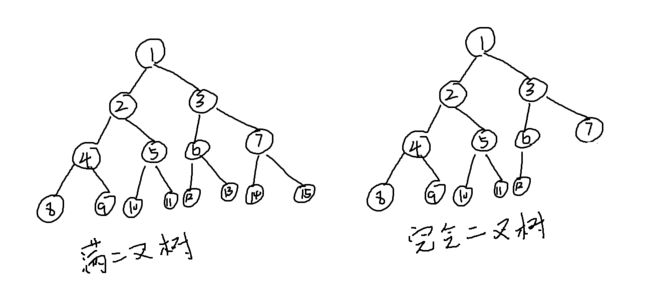
满二叉树
高度为h的,含有2^h-1个结点
若从1开始,自上而下,自左向右对结点编号,i结点的父节点为i/2向下取整,左孩子2i,右孩子2i+1
完全二叉树
每个结点的编号都与与其同高度的满二叉树一致
1.若i<=n/2向下取整,则i为分支结点,否则为叶子结点
2.叶子结点只可能在层次最大的两层上出现。对于最大层次中的叶子结点,都依次排列在该层的最左边
3.若有度为1的结点,则只可能有一个,且该结点只有左孩子
4.按层序编号后,一旦出现某编号为i的结点为叶子结点或只有左孩子,则编号大于i的结点均为叶子结点
5.若n为奇数则每个分支结点都既有左节点又有右节点
6.i所在的层次为:向下取整(log(2)i)+1
7.具有n个结点的完全二叉树的高度为:向上取整(log(2)(n+1))或向下取整(log(2)n)+1
二叉排序树
左子树上的所有结点的关键字均小于根结点的关键字,右子树上所有结点的关键字均大于根结点的关键字。左子树和右子树又各是一颗二叉排序树。
平衡二叉树
任一结点的左子树和右子树的深度之差不超过1
二叉树的性质
1.度为0,1,2的结点个数分别为n0,n1,n2
结点数(n0+n1+n2)-1=分支数=n1+2*n2
-》n0=n2+1(叶节点数)
2.非空二叉树第k层上至多有2^(k-1)个结点
二叉树的存储结构
完全二叉树和满二叉树比较适合顺序存储,通过序号来反映父子关系
二叉树一般采用链式存储结构
typedef struct BiTNode
{
ElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
在含有n个结点的二叉链表中,含有n+1个空链域。
二叉树的遍历
按照根结点被访问的时机,分为先序NLR,中序LNR,后序LRN
递归
void PreOrder(BiTree T)
{
if(T!=NULL){
visit(T);
PreOrder(T->lchild);
PreOrder(T->rchild);
}
}
每个结点都访问一次仅访问一次所以时间复杂度为O(n)
递归栈的深度恰好为树的深度
非递归
void InOrder2(BiTree T)
{
InitStack(S); BiTree p=T;
while(p||!IsEmpty(S))
{
if(p){
Push(S,p);
p=p->lchild;
}
else{
Pop(S,p); visit(p);
p=p->rchild;
}
}
}
p首先指向根节点,将p入栈,并使p指向其左节点,若p为null(没有左节点),则出栈并访问,再将p指向其右节点。
后序的非递归
因为在左,右子树都处理完毕之前不可将根从栈中移除,则需要在入栈时添加额外信息rvisited来标识,是从左子树回来的还是从右树回来的。
typedef struct{
BTNode *p;
int rvisited; //为1的时候代表p所指向的结点的右节点已被访问过
}SNode; //栈中的结点定义
typedef struct{
SNode Elem[maxsize]
int top;
}SqStack; //栈结构体
void PostOrder2(BiTree T)
{
SNode sn;
BTNode *pt=T
InitStack(S);
while(T){ //向左走到尽头,并把路径上的元素全部入栈
Push(pt,0);
pt=pt->lchild;
}
while(!S.IsEmpty()){
sn=S.getTop();
//栈顶结点的左子树一定是已经遍历完了
//因为左子树上的结点一定在它的上面
if(sn.p->rchild==NULL||sn.rvisited){
//若栈顶元素无rchild或rchild已被访问过,则出栈并访问它
Pop(S, pt);
visit(pt);
}
else{
//如果有rchild且未被访问,则去访问它的rchild
sn.rvisited=1;
pt=sn.p->rchild;
while(pt!=NULL){
Push(pt, 0);
pt=pt->lchild;
}
}
}
}
层次遍历
void LevelOrder(BiTree T)
{
InitQueue(Q);
BiTree p;
EnQueue(Q,T);
while(!IsEmpty(Q)){
DeQueue(Q,p);
visit(p);
if(p->lchild!=NULL)
EnQueue(Q,p->lchild);
if(p->rchild!=NULL)
EnQueue(Q,p->rchild);
}
}
由遍历序列构造二叉树
由二叉树的先序序列和中序序列可以唯一确定一棵二叉树
由二叉树的后序序列和中序序列可以唯一确定一棵二叉树
由二叉树的层序序列和中序序列可以唯一确定一棵二叉树
由二叉树的先序序列和后序序列不可以唯一确定一棵二叉树
二叉树遍历的应用
求二叉树的高度
递归 H=max(Hl+Hr)+1
int PostOrderGetHeight(BinTree BT)
{
int Hl,Hr,maxH;
if(BT){
Hl=PostOrderGetHeight(BT->left);
Hr=PostOrderGetHeight(BT->right);
maxH=(Hl>Hr)?Hl:Hr;
return (maxH+1);
}
else return 0;
}
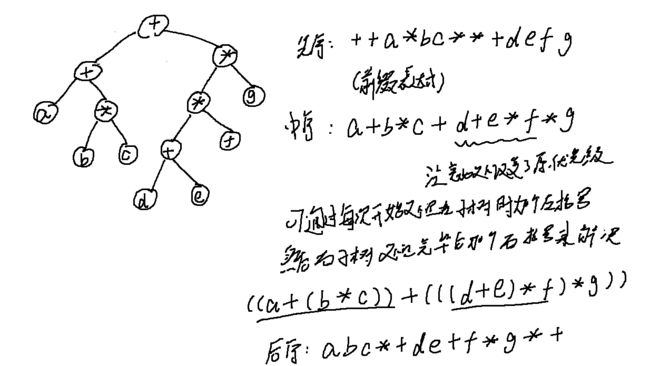
二元运算表达式及其遍历
用后缀表达式构造一棵树
思路类似用后缀表达式求值
依次读取,若遇到操作数,则建立一个单节点树并入栈,若遇到操作符,建立一个单节点,则从栈中弹出栈顶的两棵树T1,T2,将该节点作为根,T2,T1作为左右子树,再将这个树入栈
树和森林
**树的存储结构
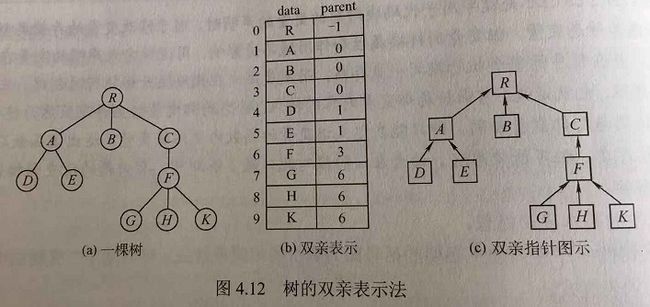
1.双亲表示法
采用一组连续空间来存储每个结点,在每个结点中增设一个伪指针,指示双亲结点在数组中的位置
#define MAX_TREE_SIZE 100
typedef struct{
ElemType data;
int parent;
}PTNode;
typedef struct{
PTNode nodes[MAX_TREE_SIZE];
int n;
}PTree;
可快速找到父节点但求子节点时需遍历整个结构
2.孩子表示法
将每个结点的孩子结点都用单链表链接起来形成一个线性结构
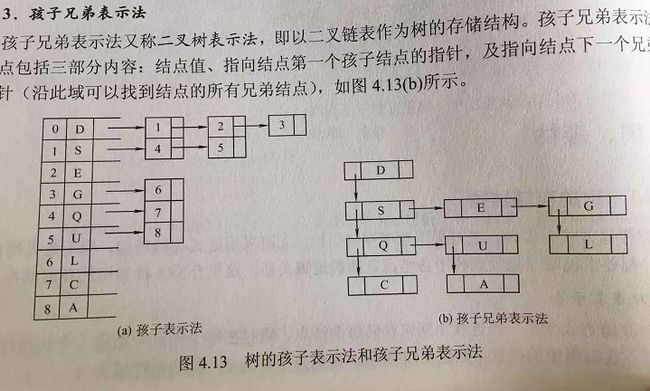
3.孩子兄弟表示法
又称二叉树表示法
每个结点包括三部分:结点值,指向结点第一个孩子结点的指针,指向结点下一个兄弟结点的指针
typedef struct CSNode{
ElemType data;
struct CSNode *firstchild, *nextsibling;
}CSNode, *CSTree;
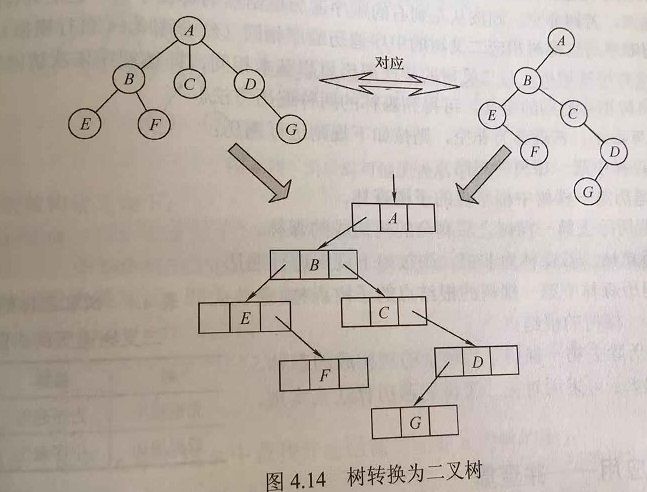
树,森林与二叉树的转换
树和森林的遍历
树的遍历
先根遍历:若树非空,则先访问根结点,再按从左到右的顺序遍历根结点的每棵子树,其访问顺序与这棵树相应二叉树的先序遍历顺序相同。
后根遍历:若树非空,则按从左到右的顺序遍历根结点的每棵子树,之后再访问根结点。其访问顺序与这棵树对应的二叉树的中序遍历相同。
森林的遍历
树的应用——并查集
有一些元素,各自为一个集合,若元素A与元素B有关系,则把它们并到同一集合,若A和C也有关系,就把C集合与之前AB合并后的集合合并。最后同一集合中的任意两个元素都是有关系可连通的。
并查集是一种集合表示,支持以下三种操作
1.Union(S, Root1, Root2)
把集合S中的子集合Root2并入Root1中,Root1与Root2互不相交
2.Find(S, x)
查找集合S中单元素x所在的子集合
3.Initial(S)
将集合S中的每个元素初始化为只有一个单元素的子集合
通常用双亲表示法作为并查集额存储结构,每个子集以一棵树表示。
初始化时每个元素自成一个单元素子集合
用数组存储
typedef struct{
ElementType Data;
int Parent;
}SetType;
查找某元素所在的集合
int Find(SetType S[], ElementType X)
{
int i;
for(i=0;i=MaxSize) return -1; //cannot find
for(;S[i].parent>=0;i=S[i].parent);
return i;
}
集合的并运算
void Union(SetType S[], ElementType X1, ElementType X2)
{
int Root1,Root2;
Root1=Find(S, X1); Root2=Find(S, X2);
if(Root1!=Root2)
S[Root2].parent=Root1;
}
数越深Find就越耗时,所以合并时尽量让小的树的parent指向大的树的根,改进方法是根节点的parent不再为-1而是数中元素个数的负值