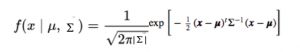介绍
我很喜欢研究无监督学习问题。它们为监督学习问题提供了一个完全不同的挑战,用我拥有的数据进行实验的发挥空间要比监督学习大得多。毫无疑问,机器学习领域的大多数发展和突破都发生在无监督学习领域。
无监督学习中最流行的技术之一就是聚类。这是一个我们通常在机器学习的早期学习的概念,它很容易理解。我相信你曾经遇到过,甚至参与过顾客细分、购物篮分析等项目。
但问题是聚类有很多方面。它并不局限于我们之前学过的基本算法。它是一种强大的无监督学习技术,我们可以在现实世界中准确地使用它。
高斯混合模型就是我想在本文中讨论的一种聚类算法。
想预测一下你最喜欢的产品的销售情况吗?或许你想通过不同客户群体的视角来理解客户流失。无论用什么方法,你都会发现高斯混合模型非常有用。
在本文中,我们将采用自下而上的方法。因此,我们首先来看一下聚类的基础知识,包括快速回顾一下k-means算法。然后,我们将深入讨论高斯混合模型的概念,并在Python中实现它们。
目录
- 聚类简介
- k-means聚类简介
- k-means聚类的缺点
- 介绍高斯混合模型
- 高斯分布
- 期望最大化EM算法
- 高斯混合模型的期望最大化
- 在Python中实现用于聚类的高斯混合模型
聚类简介
在我们开始讨论高斯混合模型的实质内容之前,让我们快速更新一些基本概念。
注意:如果你已经熟悉了聚类背后的思想以及k-means聚类算法的工作原理,那么你可以直接跳到第4部分“高斯混合模型介绍”。
那么,让我们从正式定义核心思想开始:
聚类是指根据相似数据点的属性或特征将它们分组在一起。
例如,如果我们有一组人的收入和支出,我们可以把他们分成以下几组:
- 赚得多,花得多
- 赚得多,花得少
- 赚得少,花得少
- 赚得少,花得多
这些组中的每一个都拥有一个相似的特征,在某些情况下特别有用。例如信用卡、汽车/房产贷款等等。用简单的话说:
聚类背后的思想是将数据点分组在一起,这样每个单独的簇拥有最相似的点。
有各种各样的聚类算法。最流行的聚类算法之一是k-means。让我们了解一下k-means算法是如何工作的,以及在哪些情况下该算法可能达不到预期效果。
k-means聚类简介
k-means聚类是一种基于距离的算法。这意味着它试图将最近的点分组形成一个聚类。
让我们仔细看看这个算法是如何工作的。这将建立基础知识,以帮助你了解高斯混合模型将在本文后面的地方发挥作用。
因此,我们首先定义我们想要将种群划分成的组的数量——这是k的值。基于我们想要的聚类或组的数量,然后我们随机初始化k个中心体。
然后将这些数据点分配给到离它最近的簇。然后更新中心,重新分配数据点。这个过程不断重复,直到簇的中心的位置不再改变。
注意:这是k-means聚类的简要概述,对于本文来说已经足够了。
k-means聚类的缺点
k-means聚类概念听起来很不错,不是吗?它易于理解,相对容易实现,并且可以应用于相当多的用例中。但也有一些我们需要注意的缺陷和限制。
让我们以上面看到的收入-支出的例子为例。k-means算法似乎运行得很好,对吧?等等——如果你仔细观察,你会发现所有的聚类都是圆形的。这是因为聚类的中心体是使用平均值迭代更新的。
现在,考虑下面这个点的分布不是圆形的例子。如果我们对这些数据使用k-means聚类,你认为会发生什么?它仍然试图以循环方式对数据点进行分组。这不是很好。
因此,我们需要一种不同的方法来为数据点分配聚类。因此,我们将不再使用基于距离的模型,而是使用基于分布的模型。高斯混合模型介绍基于分布的模型!
高斯混合模型简介
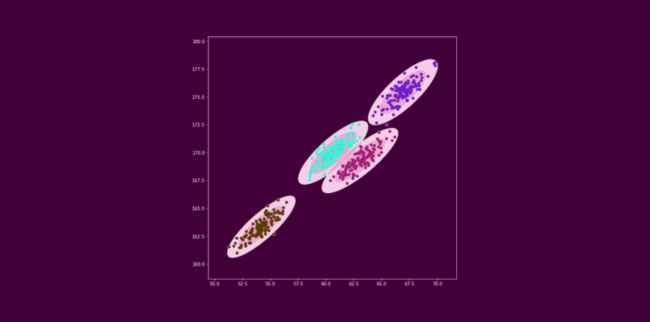
高斯混合模型(GMMs)假设存在一定数量的高斯分布,每个分布代表一个簇。因此,高斯混合模型倾向于将属于单一分布的数据点聚在一起。
假设我们有三个高斯分布(下一节会详细介绍)——GD1、GD2和GD3。均值为(μ1、μ2、μ3)和方差分别(σ1、σ2、σ3)值。对于给定的一组数据点,我们的GMM将识别属于这些分布的每个数据点的概率。
等一下,概率?
你没看错!混合高斯模型是概率模型,采用软聚类方法将点分布在不同的聚类中。我再举一个例子,这样更容易理解。
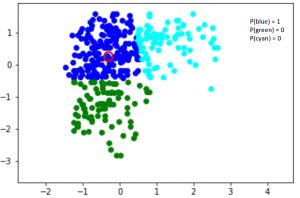
这里,我们有三个用三种颜色表示的聚类——蓝色、绿色和青色。让我们以红色突出显示的数据点为例。这个点是蓝的一部分的概率是1,而它是绿色或青色的一部分的概率是0。
现在,考虑另一个点,在蓝色和青色之间的某个地方(在下面的图中突出显示)。这个点是绿色的概率是0。这个点属于蓝色和青色的概率分别是0.2和0.8。
高斯混合模型使用软聚类技术将数据点分配给高斯分布。
高斯分布
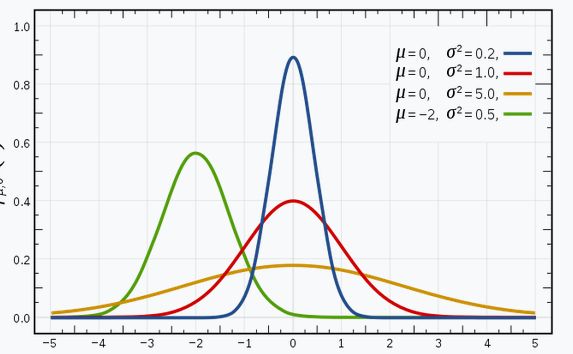
我相信你们对高斯分布(或正态分布)很熟悉。它有一个钟形曲线,数据点对称分布在平均值周围。
以下图片有几个高斯分布的不同均值(μ)和不同方差(σ2)的正态分布图像。记住,σ值越低图像越尖:
在一维空间中,高斯分布的概率密度函数为:
其中μ是均值和σ2是方差。
但这只对一维情况下成立。在二维的情况下,我们不再使用2D钟形曲线,而是使用3D钟形曲线,如下图所示:
概率密度函数为:
其中x是输入向量,μ是2维的均值向量,Σ是2×2的协方差矩阵。协方差定义了曲线的形状。我们可以推广d维的情况。
因此,这个多元高斯模型x和μ向量长度都是d,Σ是dxd的协方差矩阵。
因此,对于一个具有d个特征的数据集,我们将有k个高斯分布的混合(其中k等于簇的数量),每个都有一个特定的均值向量和协方差矩阵。但是等一下,如何分配每个高斯分布的均值和方差值?
这些值是使用一种称为期望最大化(EM)的技术确定的。在深入研究高斯混合模型之前,我们需要了解这种技术。
期望最大化EM算法
期望最大化(EM)是一种寻找正确模型参数的统计算法。我们通常在数据缺少值时使用EM,或者换句话说,在数据不完整时会使用EM算法。
这些缺失的变量被称为隐变量。在处理无监督学习问题时,我们认为目标(或簇数量)是未知的。
由于缺少这些变量,很难确定正确的模型参数。可以这样想——如果你知道哪个数据点属于哪个簇,那么就可以轻松地确定均值向量和协方差矩阵。
由于我们没有隐变量的值,期望最大化尝试使用现有的数据来确定这些变量的最佳值,然后找到模型参数。根据这些模型参数,我们返回并更新隐变量的值,等等。
广义上,期望最大化算法有两个步骤:
- E步:在此步骤中,可用数据用于估计(猜测)缺失变量的值
- M步:根据E步生成的估计值,使用完整的数据更新参数
期望最大化是许多算法的基础,包括高斯混合模型。那么,GMM如何使用EM的概念呢?我们如何将其应用于给定的点集呢?让我们来看看!
高斯混合模型的期望最大化
让我们用另一个例子来理解它。我想让你在阅读的过程中把这个思路具体化。这将帮助你更好地理解我们在谈论什么。
假设我们需要分配k个簇。高斯分布,这意味着有k个均值μ1,μ2,. .μk和协方差矩阵Σ1,Σ2,. .Σk。此外,还有一个用于分布的参数,用于定义各个分布的权重,权重代表每个簇的点的数量,用Πi表示。
现在,我们需要找到这些参数的值来定义高斯分布。我们已经确定了簇的数量,并随机分配平均值、协方差和权重。接下来,我们将执行E步和M步!
E步:
对于每个点xi,计算它属于分布c1, c2,…ck的概率。这是使用以下公式:
当将该点分配给正确的簇时,此值将比较高,否则将比较低。
M步:
E步后,我们回去更新Π,μ和Σ值。这些资料的更新方式如下:
- 新的权重定义为簇内数据的数量与数据总数量之比:
- 均值和协方差矩阵根据分配给分布的值更新,与数据点的概率值成比例。因此,一个更有可能成为该分布一部分的数据点将有更大贡献:
基于此步骤生成的更新值,我们计算每个数据点的新概率,并迭代更新这些值。重复这个过程是为了使对数似然函数最大化。实际上我们可以说
k-means只考虑更新簇中心的均值,而GMM则考虑数据的均值和方差。
在Python中实现高斯混合模型
是时候深入研究代码了!这是任何文章中我最喜欢的部分之一,所以让我们开始吧。
我们将从加载数据开始。这是我创建的一个临时文件-你可以从这个链接下载数据:https://s3-ap-south-1.amazonaws.com/av-blog-media/wp-content/uploads/2019/10/Clustering_gmm.csv。
import pandas as pd
data = pd.read_csv('Clustering_gmm.csv')
plt.figure(figsize=(7,7))
plt.scatter(data["Weight"],data["Height"])
plt.xlabel('Weight')
plt.ylabel('Height')
plt.title('Data Distribution')
plt.show()
这就是我们的数据。我们先在这个数据上建立一个k-means模型:
#训练k-means模型
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=4)
kmeans.fit(data)
#kmeans预测
pred = kmeans.predict(data)
frame = pd.DataFrame(data)
frame['cluster'] = pred
frame.columns = ['Weight', 'Height', 'cluster']
#输出结果
color=['blue','green','cyan', 'black']
for k in range(0,4):
data = frame[frame["cluster"]==k]
plt.scatter(data["Weight"],data["Height"],c=color[k])
plt.show()
结果不大准确。k-means模型未能识别正确的簇。我们仔细观察位于中心的簇,尽管数据分布是椭圆形的,但k-means已经尝试构建一个圆形簇(还记得我们前面讨论的缺点吗?)
现在让我们在相同的数据上建立一个高斯混合模型,看看我们是否可以改进k-means:
import pandas as pd
data = pd.read_csv('Clustering_gmm.csv')
# 训练高斯混合模型
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=4)
gmm.fit(data)
#GMM预测
labels = gmm.predict(data)
frame = pd.DataFrame(data)
frame['cluster'] = labels
frame.columns = ['Weight', 'Height', 'cluster']
color=['blue','green','cyan', 'black']
for k in range(0,4):
data = frame[frame["cluster"]==k]
plt.scatter(data["Weight"],data["Height"],c=color[k])
plt.show()
这正是我们所希望的结果。在这个数据集中高斯混合模型把k-means模型打败了
结尾
这是高斯混合模型的入门教程。我在这里的目的是向你介绍这种强大的聚类技术,并展示它与传统算法相比是多么有效和高效。
我鼓励你着手一个聚类项目,并在那里尝试GMMs。这是学习和强化一个概念的最好方法,相信我,你会充分认识到这个算法有多么有用。