树

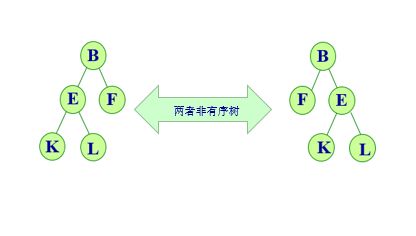
自由树：
一棵自由树 可定义为一个二元组

其中 V = {v1, ..., vn} 是由 n (n＞0) 个元素组成的有限非空集合，称为顶点集合。是n-1个序对的集合，称为边集合，E 中的元素 (vi, vj）称为边或分支。

image.png

有根数

树（Tree）是n（n>=0）个结点的有限集。
1、当n=0 时，称该树为空树；

2、在任意一棵非空树中：

（1）有且仅有一个特定的称为根（Root）的结点；

（2）当n>1时，其余结点可分为m（m>0）个互不相交的有限集T1，T2，...，Tn，其中每个集合本身又是一棵树，并称为根的子树（SubTree）
有根数记做：

image.png

注： 是一个特定的称为根(root)的结点，它只有直接后继，但没有直接前驱；

根以外的其他结点划分为 m (m ≥ 0) 个互不相交的有限集合，每个集合又是一棵树，并且称之为根的子树。

每棵子树的根结点有且仅有一个直接前驱，但可以有0个或多个直接后继。

image.png

1、基本术语：

树顶端的节点称为根，一棵树只有一个根

树中的独立单元。包含一个数据元素和若干指向其子树的分支

每个节点（除了根）都恰好有一条边向上连接到另外一个节点，上面的这个节点就成为下面结点的父节点

每个节点都可能有一条或多条边向下连接其它节点，下面这些节点就称为它的子节点

没有子节点的节点称为叶子节点或简称叶节点（度为0的结点即为叶结点，亦称为终端结点）。
。
每个节点都可以作为子树的根。

若结点的子树非空，结点子树的根即为该结点的子女

若结点有子女，该结点是子女双亲

同一结点的子女互称为兄弟。

双亲在同一层次的结点，互为堂兄弟

image.png

从根结点到该结点的路径上的所有结点都是该结点的祖先。

某结点的所有下属结点，都是该结点的子孙。

度不为0的结点即为分支结点，亦称为非终端结点。

有两种度“结点的度”与“树的度”。结点的度指的是一个结点子树的个数；树的度是指树中结点度的最大值。*

树的度

规定根结点在第一层，其子女结点的层次等于它的层次加一。以下类推。

结点的深度即为结点的层次；离根最远结点的层次即为树的深度（树中结点的最大层数）。

image.png

规定叶结点的高度为1，其双亲结点的高度等于它的高度加一。

树中结点的各棵子树 T0, T1, …是有次序的，即为有序树。

树中结点的各棵子树之间的次序是不重要的，可以互相交换位置。

image.png

n棵互不相交的树

树的存储方式

：以双亲作为索引的关键词的一种存储方式。

// 双亲表示法
#define MAX_TREE_SIZE 100
typedef int ElemType;
typedef struct PNode{
    ElemType data;//结点数据
    int parent;//双亲下标
}PTNode;
typedef struct{
    PTNode nodes[MAX_TREE_SIZE];
    int root;//根位置
    int num;//结点数目
}PTree;

特点：
根据parent指针可以找到他的双亲，时间复杂度为O(1),当parent索引为-1时，该结点即为根结点
但是要找到某结点的孩子是什么，则需要遍历这个树结构。
改进方法

兄弟之间的关系：

树中每个结点可能有多个子树，考虑用多重链表来实现
方案一：根据树的度声明足够空间，存放子树指针的节点，缺点：空间浪费

方案二：

// 双亲孩子表示法
#define MAX_TREE_SIZE 100
typedef int ElemType;
//孩子节点
typedef struct CNode{
    int child;//孩子节点的下标
    struct CNode *next;//指向下一个节点的指针
}*PChild;
//表头结构
typedef struct PNode{
    ElemType data;//结点数据
    int parent;//双亲下标
    PChild firstChilder;//指向该节点的第一个孩子结点指针
}PTNode;
//树结构
typedef struct{
    PTNode nodes[MAX_TREE_SIZE];
    int root;//根位置
    int num;//结点数目
}PTree;

二叉树

一棵二叉树是结点的n（n>=）个结点有限集合，该集合或者为空，或者是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成。

image.png

1、每个结点最多有两颗子树（没有子树或者一颗子树也可以）。
2、左子树、右子树是有顺序的，次序不能颠倒。
3、即使某一结点只有一颗子树，也要区分左右。

二叉树基本术语

若一棵二叉树中的结点,或者为， 或者,并且叶结点都集中在二叉树的.这样的二叉树为满二叉树.
特点：
1、叶子结点只能出现在最下一层
2、非叶子节点的度一定为2
3、在深度相同的二叉树中，满二叉树的节点个数一定最多，同时叶子也是最多

若一棵二叉树中只有最下面两层的结点的度,并且最下面一层的结点(叶结点)都依次排列在该层从左至右的位置上。这样的二叉树为完全二叉树.
（释义2：对一颗具有n个结点的二叉树按层序编号，如果编号为i（1完全二叉树）
特点：
1、叶子结点只能出现在最下两层
2、最下层叶子一定集中在左边连续位置。
3、倒数第二层，若有叶子节点，一定都在右部连续位置。
4、如果节点度为1，则该结点只有左孩子。
5、同样结点的二叉树，完全二叉树的深度最小。
注意：满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树。

image.png

二叉树的性质

性质1：二叉树的第i层至多有个结点（i≥1）
性质2：深度为k的二叉树至多有个结点（k>1）

性质3：对任何一棵二叉树，如果其叶结点有个, 度为 2 的非叶结点有 个, 则有

推导： 若设度为 1 的结点有 个，总结点数为 ，总边数为 ，则根据二叉树的定义，

=（总边树总是等于总结点树-1）
因此，有 即：
所以：

二叉树存储结构

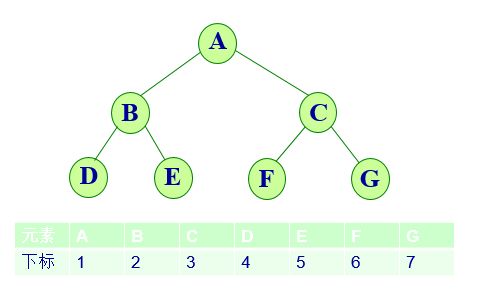
二叉树的严格定义，在数组中能直接表现出逻辑结构

使用^表示不存在的结点

斜树

会比较浪费空间，考虑使用链式结构

image.png

image.png

typedef int ElemType;
//孩子节点
typedef struct BTNode{
    ElemType data;//数据
    struct BTNode *LChild,*RChild;//左右孩子结点
}BTNode,*BTree;

是指从根结点出发，按照某种依次访问二叉树中的所有结点

1、前序遍历（Preorder Traversal）：
若二叉树为空，则空操作返回，
否则
访问根结点 (V)；
前序遍历左子树 (L)；
前序遍历右子树 (R)。

2、中序遍历：
若二叉树为空，则空操作返回，
否则
从根结点开始；
中序遍历根结点的左子树 (L)；
访问根结点 (V)；
中序遍历根结点的右子树 (R)。

3、后序遍历：
若二叉树为空，则空操作返回，
否则
后序遍历左子树 (L)；
后序遍历右子树 (R)。
访问根结点 (V)；

4、层序遍历：
若二叉树为空，则空操作返回，
否则
从树的第一层开始，从上而下逐层遍历，在同一层中，按从左到右顺序逐个访问；

代码实现：

#include 
#include 
#include 
typedef char ElemType;
//孩子节点
typedef struct BTNode{
    ElemType data;//数据
    struct BTNode *LChild,*RChild;//左右孩子结点
}BTNode,*BTree;


//创建一颗二叉树 使用前序遍历的方式输入数据
void CreateBitTree(BTree *T){
    char c;
    scanf("%c",&c);
    printf("创建");
    if(' ' == c){
        *T=NULL;

    }else{
    *T=(BTNode*)malloc(sizeof(BTNode));//根节点
    (*T)->data=c;
    CreateBitTree(&(*T)->LChild);//左节点
    CreateBitTree(&(*T)->RChild);//右节点

    }
}
void visit(ElemType data,int level){
    printf("%c位于第%d层",data,level);
}
//前序遍历二叉树
void PreOrderTraverse(BTree T,int level){
    if(T){
        visit(T->data,level);
        PreOrderTraverse(T->LChild,level+1);//遍历左子树
         PreOrderTraverse(T->RChild,level+1);//遍历右子树
    }
}


int main (){
    int level=1;
    BTree T=NULL;
    CreateBitTree(&T);
   // PreOrderTraverse(T,level);
    return 0;
  }

线索二叉树

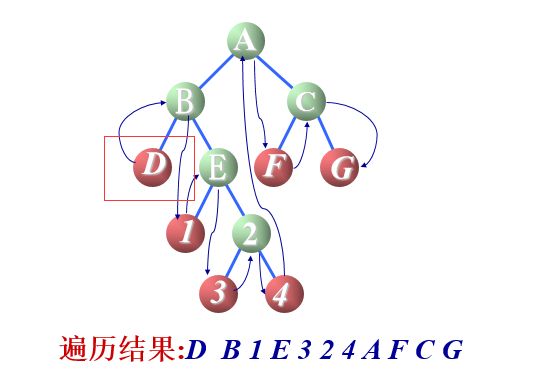
查看下图，可看到会存在^ 浪费空间。可利用^记录前驱后继

下图中使用中序遍历，没隔一个可以结点可以记录前驱后继

下面黄色表示只有一个空余，红色有两个空余

定义如下结构：

LeftTag为0时LeftChild指向该结点的左孩子，为1时指向改结点的前驱。
RigthTag为0时RightChild指向该结点的右孩子，为1时指向改结点的后继。

#include 
#include 
#include 
typedef char ElemType;
typedef enum {Link,Thread} PointTag;//线索存储枚举，为0时指向左右孩子，为1时指向前驱后继
//孩子节点
typedef struct BTNode{
    ElemType data;//数据
    struct BTNode *leftChild,*rightChild;//左右孩子结点
    PointTag leftTag;
    PointTag rightTag;

}BTNode,*BTree;
//全局变量，记录刚刚访问的前驱结点
BTree pre;

//创建一颗二叉树 使用前序遍历的方式输入数据
void CreateBitTree(BTree *T){
    char c;
    scanf("%c",&c);
    if(' ' == c){
        *T=NULL;

    }else{
    *T=(BTNode*)malloc(sizeof(BTNode));//根节点
    (*T)->data=c;
    (*T)->leftTag=Link;
    (*T)->rightTag=Link;
    CreateBitTree(&(*T)->leftChild);//左节点
    CreateBitTree(&(*T)->rightChild);//右节点

    }
}
//中序遍历线索化
void InThreading(BTree T){
    if(T){
       InThreading(T->leftChild);//线索化左子树
       if(!T->leftChild){//无左孩子，修改tag,空指针作为线索指针指向前驱节点
         T->leftTag=Thread;
         T->leftChild=pre;
       }
/*由于后继结点还没有访问到，将当前访问的结点作为pre的后继结点*/
       if(!pre->rightChild){//无右孩子，修改tag
            pre->rightTag=Thread;
            pre->rightChild=T;
       };
       pre=T;//  更新pre
       InThreading(T->rightChild);//线索化右子树
    }
}
//将树线索化，加上头结点，确保pre初始化
void InOrderThreading(BTree *p,BTree T){
    *p=(BTNode*)malloc(sizeof(BTNode)); //  生成头结点
    (*p)->leftTag=Link;//  头结点左孩子即是树的根结点，所以左标记为Link
    (*p)->rightTag=Thread;// 头结点右孩子指向中序遍历的最后一个元素，是线索指针
    (*p)->rightChild=*p;//  初始化将p的右孩子回指
    if(!T){
        (*p)->leftChild=T; //如果树为空，头结点左孩子也回指
    }else{
        (*p)->leftChild=T;//根结点挂载到头结点的左子树
        pre=*p; //  pre先指向p，这样中序遍历的第一个结点原本指向空，现在可以指向头结点
        InThreading(T);//将树线索化
        pre->rightChild=*p; //  线索化后pre指向中序遍历的最后一个结点，所以该结点的右孩子原本指空，现在作为线索结点指向头结点
        pre->rightTag=Thread;
        (*p)->rightChild=pre; // 头结点的有孩子指向中序遍历的最后结点pre
    }
}
//中序遍历二叉树
void InOrderTraverse(BTree T){
    BTree p;
    p=T->leftChild;//  头结点的左孩子为树的根结点
    while(p!=T){//如果p不等于T,循环 当p==T时，树为空树或者遍历完毕
        while(p->leftTag == Link){//  如果左标记为Link，则一路指向左孩子
            p=p->leftChild;
        }
        printf("%c\n",p->data);// 访问到中序遍历的第一个元素
        while(p->rightTag == Thread && p->rightChild != T){//  结点为线索结点且结点右孩子不等于头结点
            p=p->rightChild; /*遍历线索路线*/
            printf("%c\n",p->data);
        }
/*p的右标记是孩子标记，转到右孩子继续遍历 或者 p的右孩子指向头结点，p指向头结点，遍历结束*/
        p=p->rightChild;
    }

}

int main (){
    BTree p,T=NULL;
    CreateBitTree(&T);
    InOrderThreading(&p,T);
    InOrderTraverse(p);
    return 0;
  }

哈夫曼（huffman）树和哈夫曼编码

结点的路径长度：从根结点到该结点的路径上的连接数。
数的路径长度：树中每个叶子节点的路径长度之和。
结点带权路径长度：结点的路径长度与结点权值的乘积。
树的带权路径长度：WPL(Weight Path Length)是树中所有叶子结点带权路径长度之和。

定长编码：ASCII编码
变长编码：单个编码的长度不一致，可以根据整体频率来调节。
前缀码：没有任何码字是其他码字的前缀。