1.算法概述
邻近算法,或者说K最近邻(kNN,k-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一。所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用它最接近的k个邻居来代表。
kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 kNN方法在类别决策时,只与极少量的相邻样本有关。由于kNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,kNN方法较其他方法更为适合。
2.算法特点
KNN近邻算法(监督学习-分类方法)
优点:精度高,对异常值不敏感、无数据输入假定。
缺点:计算复杂度高、空间复杂度高
适用数据范围:数值型和标称型数值型:连续型数据(变量可从无限的数字集合中取值)
标称型:离散型数据(变量可从有限的集合中取值)
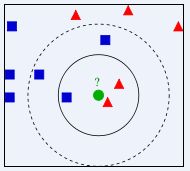
当K为3时,绿色圆圈的分类应为红色三角形
当K为5时,绿色圆圈的分类应为蓝色正方形注意1:K一般取值不大于20.k作为参数对模型的拟合度变化有很大的影响。
3.KNN的一般流程
4. 实例解释
4.1 安装KNN包
4.2 修改实例代码
随包提供的KNN.py代码是基于Python2.6版本的,在我3.6.3版本上运行时会出现代码不兼容的问题、需要修改3.0版本的兼容问题
Python3.0版本不再对空格缩进进行兼容、统一使用tab缩进。
Python3.0版本的Print函数都需要用括号引入
4.3 实例背景
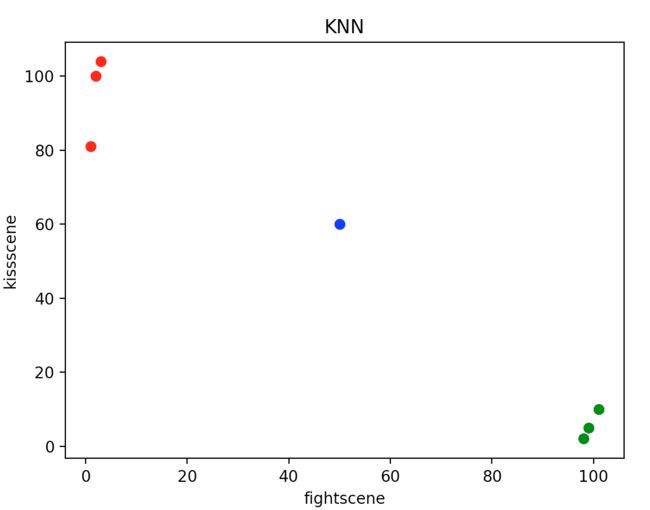
以电影分类为例子,使用k-近邻算法分类爱情片和动作片。有人曾经统计过很多电影的打斗镜头和接吻镜头,下图显示了6部电影的打斗和接吻镜头数。 假如有一部未看过的电影,如何确定它是爱情片还是动作片呢?
①首先需要统计这个未知电影存在多少个打斗镜头和接吻镜头,下图中问号位置是该未知电影出现的镜头数
②之后计算未知电影与样本集中其他电影的距离(相似度),具体算法先忽略,结果如下表所示:
③将相似度列表排序,选出前k个最相似的样本。此处我们假设k=3,将上表中的相似度进行排序后前3分别是:He’s Not Really into Dudes,Beautiful Woman,California Man。
④统计最相似样本的分类。此处很容易知道这3个样本均为爱情片。
⑤将分类最多的类别作为未知电影的分类。那么我们就得出结论,未知电影属于爱情片。
4.4 代码示例
代码已上传至github仓库
import KNN
import matplotlib.pyplot as plt
import operator
from numpy import *
def create_data():
# 训练数据
# [Movie Title] [number of FightScene] [number of KissScene] [Type]
# California Man 3 104 LOVE
# He's Not Realy int Dudes 2 100 LOVE
# Beatiful Women 1 81 LOVE
# Kevin LongBlade 101 10 ACTION
# Robo Slayer 3000 99 5 ACTION
# Amped 2 98 2 ACTION
# ? 18 90
group = array([[3, 104], [2, 100], [1, 81], [101, 10], [99, 5], [98, 2]])
labels = ['LOVE', 'LOVE', 'LOVE', 'ACTION', 'ACTION', 'ACTION']
return group, labels
def demo():
group, labels = create_data()
# [[3 104]
# [2 100]
# [1 81]
# [101 10]
# [99 5]
# [98 2]]
# print(group)
# ['LOVE', 'LOVE', 'LOVE', 'ACTION', 'ACTION', 'ACTION']
# print(labels)
# 使用模型
title = input("请输入电影的名字")
number_of_fight_scene = int(input("请输入打斗场面的镜头数(0-1000)"))
number_of_kiss_scene = int(input("请输入亲吻场面的镜头数(0-1000)"))
show_figure([number_of_fight_scene, number_of_kiss_scene], group)
predicate = classify([number_of_fight_scene, number_of_kiss_scene], group, labels, 3)
print('%s 的类型为 %s' % (title, predicate))
def show_figure(inX, dataSet):
# 输入数据的分布状况
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.scatter(dataSet[:, 0][0:3], dataSet[:, 1][0:3], c='r', marker='o')
ax.scatter(dataSet[:, 0][3:6], dataSet[:, 1][3:6], c='g', marker='o')
ax.scatter(inX[0], inX[1], c='b', marker='o')
plt.xlabel('fightscene')
plt.ylabel('kissscene')
plt.title('KNN')
plt.show()
def classify(inX, dataSet, labels, k):
# KNN的主要实现方法
# 下面的求距离过程就是按照欧氏距离的公式计算的。
# 即 根号(x^2+y^2)
# [50, 60]
print(inX)
# 获取训练样本的大小
dataSetSize = dataSet.shape[0]
# tile属于numpy模块下边的函数
# tile(A, reps)返回一个shape=reps的矩阵,矩阵的每个元素是A
# 比如 A=[0,1,2] 那么,tile(A, 2)= [0, 1, 2, 0, 1, 2]
# tile(A,(2,2)) = [[0, 1, 2, 0, 1, 2],
# [0, 1, 2, 0, 1, 2]]
# tile(A,(2,1,2)) = [[[0, 1, 2, 0, 1, 2]],
# [[0, 1, 2, 0, 1, 2]]]
diffMat = tile(inX, (dataSetSize, 1)) - dataSet
# [[47 - 44]
# [48 - 40]
# [49 - 21]
# [-51 50]
# [-49 55]
# [-48 58]]
print(diffMat)
sqDiffMat = diffMat ** 2
# [[2209 1936]
# [2304 1600]
# [2401 441]
# [2601 2500]
# [2401 3025]
# [2304 3364]]
print(sqDiffMat)
# axis=1表示按照横轴,sum表示累加,即按照行进行累加。
sqDistances = sqDiffMat.sum(axis=1)
# [4145 3904 2842 5101 5426 5668]
print(sqDistances)
distances = sqDistances ** 0.5
# [64.38167441 62.48199741 53.31041174 71.42128534 73.66138744 75.2861209 ]
print(distances)
# 按照升序进行快速排序,返回的是原数组的下标。
# 比如,x = [30, 10, 20, 40]
# 升序排序后应该是[10,20,30,40],他们的原下标是[1,2,0,3]
# 那么,numpy.argsort(x) = [1, 2, 0, 3]
sortedDistIndicies = distances.argsort()
# [2 1 0 3 4 5]
print(sortedDistIndicies)
# 存放最终的分类结果及相应的结果投票数
classCount = {}
for i in range(k):
print(sortedDistIndicies[i])
voteIlabel = labels[sortedDistIndicies[i]]
print(voteIlabel)
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
print(classCount)
# 投票过程,就是统计前k个最近的样本所属类别包含的样本个数
# 2
# LOVE
# {'LOVE': 1}
# 1
# LOVE
# {'LOVE': 2}
# 0
# LOVE
# {'LOVE': 3}
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
# 把分类结果进行排序,然后返回得票数最多的分类结果
# [('LOVE', 3)]
print(sortedClassCount)
return sortedClassCount[0][0]
if __name__ == '__main__':
demo()