数据结构课程设计(题目3)
问题描述
在一个加密应用中,要处理的信息来自下面的字符集,各个字符的相关使用频度如下:
字符空格 A B C D E F G H I J K L M
频度 180 64 13 23 3210322 15 4757 15 31 20
字符 N O P Q R S T U V W X Y Z
频度 55 63 151 48 56 80 25 7 18 2 16 1
现请编写程序你实现如下功能:
(1)运行时,由用户输入来初始化字符集大小和相应用字符。
(2)输入一个要加密的字符串,将其加密。
(3)输出解密字符串。
问题分析
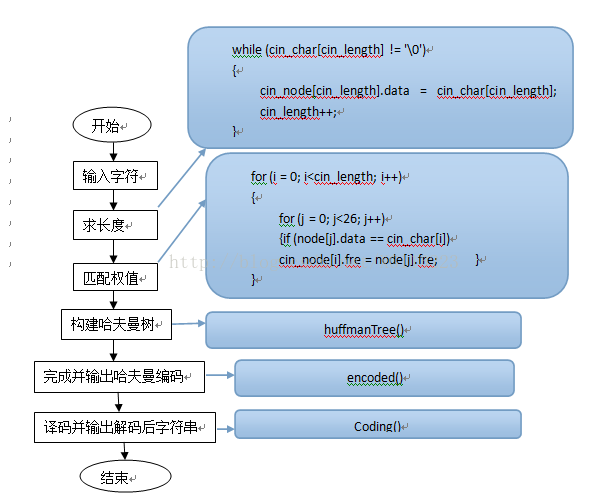
(1)定义一个结构体Node_datafre,用该结构体中的char data,int fre分别来存放初始化的字符及其对应的权值。再定义一个变量名为Node_huffman的结构体,用该结构体中的int lchild、int rchild、int parent、int weight、int flag分别表示哈夫曼树中每个结点的左孩子、右孩子、双亲结点、权 值、标示被挑出来的两个最小的数,
(2)编写init()函数实现字符及其频率(权值)的初始化。
(3)编写select()和huffmanTree()函数来对字符的权值进行排序并构造一棵哈夫曼树。
(4)编写encoded()函数来求哈夫曼编码和哈夫曼编码的输出。
逻辑结构与逻辑设计
主函数流程图及所调用的函数如下所示:
算法分析
haffman树
(1) haffman树的类型
structNode_huffman
{
int lchild;
int rchild;
int parent;
int weight;
int flag;
} huffTree[2 * M- 1];//哈夫曼树的节点
(2) haffman树构造算法
void select()
{
int i,j;
int t;
int min1;
for (i = 0; i<2; i++)
{
j = 0;
while (huffTree[j].flag == 1)
j++;
min1 = j;
for (j = min1 + 1; j<2 *cin_length - 1; j++)
{
if (huffTree[j].flag == 0)
{
if(huffTree[min1].weight>huffTree[j].weight)
min1 =j;
}
}
min[i] = min1;
t = min[i];
huffTree[t].flag = 1;
}
}
voidhuffmanTree()
{
int i, k, t;
int i1, i2;
for (i = 0; i<2 * cin_length - 1; i++)
{
huffTree[i].parent = -1;
huffTree[i].lchild = -1;
huffTree[i].rchild = -1;
huffTree[i].flag = 0;
}
for (i = 0; i huffTree[i].weight =cin_node[i].fre; for (i = cin_length; i<2 * cin_length - 1;i++) huffTree[i].weight = N; for (k = cin_length, t = cin_length; k<2 *cin_length - 1; k++, t--) { select(); i1 = min[0]; i2 = min[1]; //cout << i1 <<" " << i2 << endl; huffTree[i1].parent = k; huffTree[i2].parent = k; huffTree[k].weight =huffTree[i1].weight + huffTree[i2].weight; huffTree[k].lchild = i1; huffTree[k].rchild = i2; } } (3) haffman编码 void encoded() { int i, j; for (i = 0;i { for(j = 0; j code[i][j]= -1; } int par,child; for (i = 0;i { j =0; child= i; par= huffTree[child].parent; while(par != -1) { if(huffTree[par].lchild == child) code[i][j]= 0; elseif (huffTree[par].rchild == child) code[i][j]= 1; child= par; par= huffTree[par].parent; j++; } } for (i = 0;i { for(j = M - 2; j>-1; j--) { if(code[i][j] != -1) cout<< code[i][j]; } //cout<< endl; } } 1,算法的时间复杂度分析:由于本程序部分用了双循环嵌套结构,故为O(n^2), 2,算法的空间复杂度分析: O(n)。 #include #include using namespace std; #define M 10 #define N 200 struct Node_datafre { chardata; intfre; }node[26], cin_node[M];//放的是目标数组的对应数据 struct Node_huffman { intlchild; intrchild; intparent; intweight; intflag; } huffTree[2 * M - 1];//哈夫曼树的节点 int cin_length; char a[26] = { 'a', 'b', 'c', 'd', 'e','f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u','v', 'w', 'x', 'y', 'z' }; int b[26] = { 180, 64, 13, 23, 32, 103, 22,15, 47, 57, 15, 31, 20, 55, 63, 15, 1, 48, 56, 80, 25, 7, 18, 2, 16, 1 }; int code[M][M - 1];//存放编码 int min[2] = { 0, 0 }; void init() { inti; for(i = 0; i<26; i++) { node[i].data= a[i];//字符初始化 node[i].fre= b[i];//频率初始化 } } //hafuman void select()//将要处理的节点的huffman[m],此算法为动态查找最小的两个 { int i, j; intt; intmin1; for(i = 0; i<2; i++) { j= 0; while(huffTree[j].flag == 1) j++; min1= j; for(j = min1 + 1; j<2 * cin_length - 1; j++) { if(huffTree[j].flag == 0) { if(huffTree[min1].weight>huffTree[j].weight) min1= j; } }//选择排序的思想——找出最小两个数在哈夫曼数组中相应位置,即huffTree[]相应的下标 min[i]= min1;//全局数组min[]接收最小的两个数在哈夫曼数组中相应位置,即huffTree[]相应的下标(全局数组不用传参) t= min[i]; huffTree[t].flag= 1;//flag=1就是已经被挑出来作为最小两个的其中一个 } } void huffmanTree() { inti, k, t; inti1, i2;//i1,i2表示select()找出的最小两个数的下标 for(i = 0; i<2 * cin_length - 1; i++) { huffTree[i].parent= -1; huffTree[i].lchild= -1; huffTree[i].rchild= -1; huffTree[i].flag= 0; } for(i = 0; i huffTree[i].weight= cin_node[i].fre; for(i = cin_length; i<2 * cin_length - 1; i++) huffTree[i].weight= N; for(k = cin_length, t = cin_length; k<2 * cin_length - 1; k++, t--) { select(); i1= min[0]; i2= min[1]; //cout<< i1 << " "<< i2 << endl; huffTree[i1].parent= k; huffTree[i2].parent= k; huffTree[k].weight= huffTree[i1].weight + huffTree[i2].weight; huffTree[k].lchild= i1; huffTree[k].rchild= i2; } } void encoded() { inti, j; for(i = 0; i { for(j = 0; j code[i][j]= -1; } intpar, child; for(i = 0; i { j= 0; child= i;//第i个叶子节点,第cin_llength个 par= huffTree[child].parent; while(par != -1)//从叶子节点遍历至根节点的标志 { if(huffTree[par].lchild == child) code[i][j]= 0; elseif (huffTree[par].rchild == child) code[i][j]= 1; child= par; par= huffTree[par].parent; j++; } } //定义编码输出的格式 for(i = 0; i { //倒序控制输出,并且不输出-1,即无效的编码字段 for(j = M - 2; j>-1; j--) { if(code[i][j] != -1) cout<< code[i][j]; } //cout<< endl; } } void Coding() { inti=0,j,p,leap; while(i { p=2*cin_length-2; for(j=cin_length-2;j>-1;j--) { if(code[i][j]!=-1) { if(code[i][j]==0) p=huffTree[p].lchild; else p=huffTree[p].rchild; } } leap=huffTree[p].weight; for(intk=0;k { if(cin_node[k].fre==leap) { cout< break; } } i++; } cout< } void main() { init(); inti; intj; charcin_char[M]; cout<< "请输入一个不大于10的连续的小写字符串:" << endl; cin>> cin_char; while(cin_char[cin_length] != '\0') { cin_node[cin_length].data= cin_char[cin_length];//处理cin_node[M].data cin_length++; } for(i = 0; i { for(j = 0; j<26; j++) { if(node[j].data == cin_char[i]) cin_node[i].fre= node[j].fre;//处理cin_node[M].fre } } cout< cout<<"所输入的字符及其对应的权值:"< for(j = 0; j cout<< cin_node[j].data << " " << cin_node[j].fre<< " "; cout< huffmanTree(); cout< cout<<"哈夫曼树构造过程存储空间的状态:"< cout< for(i = 0; i<2 * cin_length - 1; i++) { cout<< setw(8)< < } cout< cout<<"此字符串加密后的编码为:"< encoded(); cout< cout< cout<<"解码后字符为:"; Coding(); } 刚开始接触到这个程序设计时,便知道是与哈夫曼算法相关的一个程序,之后的一切准备也是围绕着这个重心来做的。虽然早早地确定好了设计的方向,但是等到真正要开始进行这个系统的编写时才发现还是有很多东西无从下手,也有很多相关并且要用到的知识还没有完全掌握与运用甚至于还没有完全地了解。这让我不得不重新去翻看书本去再巩固一下其中的内容,尤其是哈夫曼树构建那一块的知识。在再熟悉过书本的知识以后,我终于正式开始了这个程序的编写。在这个过程中,调试总是会出现这样那样的错误,有一些甚至完全看不错出来到底是怎么错的,只知道在那个地方有错,却不知道怎么改,于是只好不断地摸索着修改。有时候这一部分明明是没有错误的,那一部分也是没有错误的,但是同时调试的时候就是会出错,这些问题无疑给程序的编写加大了难度。除此之外,有一些看起来并不复杂的操作,其实也需要很多的算法去支持。尽管此次做课程设计未能尽如人意,但是不论如何,这次题目3程序的编写让我从中学习到了很多东西。 《数据结构(c++版)》(第二版).清华大学出版社
时间复杂度与空间复杂度分析
源代码
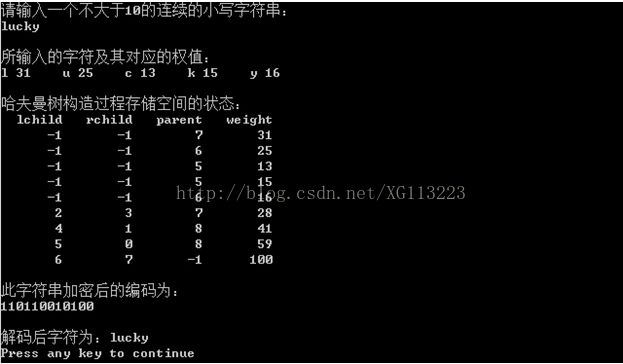
程序运行结果
心得
参考文献