二叉排序树的构造及其基本操作
二叉排序树的定义
对于一棵空的二叉树或者具有如下性质的二叉树：
1.若其左子树不为空，则左子树所有结点的值均小于根结点的值。
2.若其右子树不为空，则右子树所有结点的值均大于根结点的值。
3.其左右子树也是二叉排序树。
如：
相关图片来源《数据结构——从概念到C++实现（第三版）》
二叉排序树中对值的查找
给定一个值p,当前结点为bt,若bt->data==p,查找成功。
若pdata,则在pt左子树查找。
若p>bt->data,则在pt右子树查找。
BiNode* BiSortTree::SearchBST(BiNode* bt, datatype x)
{
if (bt == NULL) return NULL;
if (bt->data == x)return bt;
else if (bt->data > x)return SearchBST(bt->lchild, x);
else return SearchBST(bt->rchild, x);
}
插入
当root为空时直接插入。
若root不为空，模拟查找的过程找到其该插入的位置，然后插入。
BiNode* BiSortTree::InsertBST(BiNode* bt, datatype x)
{
if (bt == NULL)
{
BiNode* s = new BiNode;
s->data = x;
s->lchild = s->rchild = NULL;
bt = s;
return bt;
}
else if (bt->data > x)
{
if (bt->lchild == NULL)bt->lchild = InsertBST(bt->lchild, x);
else InsertBST(bt->lchild, x);
}
else
{
if (bt->rchild == NULL)bt->rchild = InsertBST(bt->rchild, x);
else InsertBST(bt->rchild, x);
}
}
二叉排序树的创建
其实就是一个不断插入的过程。
BiSortTree::BiSortTree(int a[], int n)
{
root = NULL;
for (int i = 0;i < n;i++)
{
if (i == 0) root = InsertBST(root, a[i]);//在插入操作时，当root节点为空时分配根节点空间，并且root的地址不会改变。
else InsertBST(root, a[i]);
}
}
删除
1.当删除的结点是叶子结点，直接删除即可。
下图中需要删除的结点为p所指，f为其双亲结点。
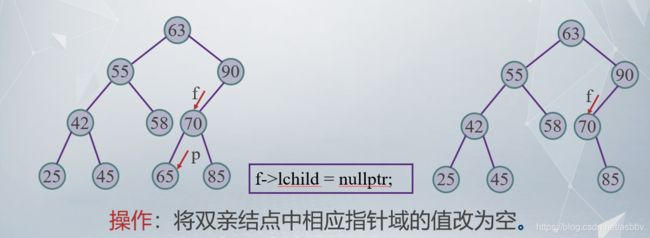2.被删除的结点只有左子树或右子树，让当前结点的左孩子或右孩子（不为空的那个）指向其左孩子或右孩子的儿子。
3.被删除的结点既有左子树又有右子树，找到左子树的最大值，与当前要删除的结点替换值，并删除之前找到的左子树的最大值。
有一个特殊情况，当左子树中的最大值结点是被删除结点的孩子。
但我们还需要解决一个问题，如果想要实现上述过程我们需要找到需要删除的结点以及需要删除结点的父亲。
在此我用一个find函数找到所要删除结点的父亲。
BiNode* BiSortTree::find(BiNode* root,const datatype key)
{
fa = NULL;
BiNode* cur = root;
while (cur != NULL && cur->data != key)
{
fa = cur;
if (key > cur->data)cur = cur->rchild;
else cur = cur->lchild;
}
if (cur == NULL)return NULL;
return cur;
}
并且对于所删除的结点是不是根结点的情况（此时father为NULL）需要特判一下，具体见代码。
void BiSortTree::DeleteBST(datatype x)
{
BiNode* p = find(x);
if ((p->lchild == NULL) && (p->rchild == NULL))
{
if (fa == NULL);
else if (fa->lchild == p)fa->lchild = NULL;
else if (fa->rchild == p)fa->rchild = NULL;
delete p;return;
}
if (p->rchild == NULL)
{
if (fa == NULL)
{
root = p->lchild;
delete p;return;
}
else
{
if (fa->lchild == p)fa->lchild = p->lchild;
else if (fa->rchild == p)fa->rchild = p->lchild;
delete p;return;
}
}
if (p->lchild == NULL)
{
if (fa == NULL)
{
root = p->rchild;
delete p;return;
}
else
{
if (fa->lchild == p)fa->lchild = p->rchild;
else if (fa->rchild == p)fa->rchild = p->rchild;
delete p;return;
}
}
BiNode* par = p, * s = p->lchild;
while (s->rchild != NULL)
{
par = s;
s = s->rchild;
}
if (par->lchild == s)par->lchild = NULL;
if (par->rchild == s)par->rchild = NULL;
p->data = s->data;
if (par == p)par->lchild = s->lchild;
else par->rchild = s->lchild;
delete s;
}
以下的操作对于二叉树同样适用
二叉排序树的前中后序的递归遍历
其实就是输出根结点的位置为前中后。
void BiSortTree::PreOrder(BiNode* bt)
{
if (bt == NULL)return;
else
{
cout << bt->data << endl;
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
}
void BiSortTree::InOrder(BiNode* bt)
{
if (bt == NULL)return;
else
{
PreOrder(bt->lchild);
cout << bt->data << endl;
PreOrder(bt->rchild);
}
}
void BiSortTree::PostOrder(BiNode* bt)
{
if (bt == NULL)return;
else
{
PreOrder(bt->lchild);
PreOrder(bt->rchild);
cout << bt->data << endl;
}
}
二叉排序树的非递归前序遍历
首先我们需要一个栈，先将root入栈，然后出栈（此时出的就是root）输出，如果有右结点则入右结点，有左节点则入左节点，注意顺序，因为是前序遍历所以让右结点先入左结点后入，这样会保证左结点先出栈，循环直到栈空。
void BiSortTree::IterativePreorder()
{
BiNode* stack[Max];
int top = -1;
if (root == NULL)return;
stack[++top] = root;
while (top!=-1)
{
BiNode* p = stack[top];
cout << p->data << endl;
top--;
if (p->rchild != NULL)stack[++top] = p->rchild;
if (p->lchild != NULL)stack[++top] = p->lchild;
}
}
二叉排序树的层序遍历
需要用到一个队列，先将根结点入队。然后将队列中的队首元素（这时就是根结点）出队、输出，再把当前出队结点的左右子节点压入队列（如果左右结点不为空的话），循环直到队列为空。
void BiSortTree::LevelOrder()
{
BiNode* Q[Max], * q = NULL;
int front = -1, rear = -1;
if (root == NULL) return;
Q[++rear] = root;
while (front != rear)
{
q = Q[++front];
cout << q->data << endl;
if (q->lchild != NULL)Q[++rear] = q->lchild;
if (q->rchild != NULL)Q[++rear] = q->rchild;
}
}
求二叉排序树的高度
DFS，先一直往左走直到尽头，再跳回往右，把所有路径遍历一遍比较得出最大的高度。
int h=0,ht=0;
void BiSortTree::get_high(BiNode* bt)
{
ht++;
if (bt == NULL)return;
if (bt->lchild == NULL && bt->rchild == NULL)
{
h = max(h, ht);
return;
}
get_high(bt->lchild);
ht--;
get_high(bt->rchild);
ht--;
}
求二叉排序树度为0、度为1、度为2的结点的个数
DFS将二叉树遍历一遍，看其左右结点是否为空逐一记录各度的结点数。
void BiSortTree::get_node(BiNode* bt)
{
if (bt->lchild != NULL && bt->rchild != NULL)
{
d2++;
get_node(bt->lchild);
get_node(bt->rchild);
}
else if (bt->lchild!=NULL)
{
d1++;
get_node(bt->lchild);
}
else if (bt->rchild != NULL)
{
d1++;
get_node(bt->rchild);
}
else
{
d0++;
return;
}
}
Code
#include码字不易给个赞吧QAQ~