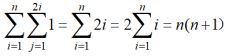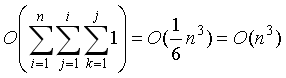时间复杂度分析(含王道绪论习题)
算法及其复杂度分析总结(含王道绪论习题)
- 一.算法
-
- 1.算法的定义
- 2.算法与程序的区别
- 二.复杂度
-
- 1.时间复杂度
- 2.大O表示法
- 3.同一问题不同算法的效率比较
- 4.复杂度计算【部分参考王道总结】
一.算法
1.算法的定义
算法是指解决问题的一种方法或一个过程。
它是若干指令的有穷序列,其中的每条指令表示一个或多个操作
满足性质:
(1)输入:有外部提供的量作为算法的输入。
(2)输出:算法产生至少一个量作为输出。
(3)确定性:组成算法的每条指令是清晰,无歧义的。
(4)有穷性:算法中每条指令的执行次数是有限的,执行每条指令的时间也是有限的。
(5)可行性:算法中描述的操作都可以通过已经实现的基本运算执行有限次实现
例1.算法应该是( )。
A.程序 B.问题求解步骤的描述 C.要满足五个基本特性 D. A和C
1. B
算法代表了对问题求解步骤的描述,而程序则是算法在计算机上的特定的实现。
五个基本特性是必要性,不能作为算法的定义。
2.算法与程序的区别
(1)算法+数据结构=程序;
(2)程序不一定满足有穷性,如死循环,操作系统等。
操作系统它是一个在无限循环中执行的程序,因而不是一个算法。【操作系统的各种任务可看成是单独的问题,每一个问题由操作系统中的一个子程序通过特定的算法来实现。该子程序得到输出结果后便终止。】
二.复杂度
1.时间复杂度
复杂度包括时间复杂度和空间复杂度,一般研究算法的时间复杂度,因为随着计算机硬件的发展,算法中数据的存储往往不是太大问题,因此算法更注重“用空间换时间”。【在时间复杂度一样的情况下,会考虑空间复杂度】
2.大O表示法
(1)大O表示时间复杂度
如果存在正的常数C和自然数N0,使得当N>=N0时有T(N)<=Cf(N),T(N)=O(f(N))则称函数T(N)当N充分大时上有界,且g(N)是它的一个上界,记为T(N)=O(f(N))。即T(N)的阶不高于f(N)的阶。
(2)渐进复杂性
取f(n)中随n增长最快的项,将其系数置为1作为时间复杂度的度量。
将O(1)、O(n)、O(logn)、O( n^2 )分别称为常数阶、线性阶、对数阶和平方阶。
O(1) 程序运行多少次跟问题的规模n无关。
(3)最坏时间复杂度
一般总是考虑在最坏情况下的时间复杂度,以保证算法的运行时间不会比它更长,即它是最坏情况下估算算法执行时间的一个上界。例如一个复杂度O(n2)的算法也可以说它是O(n3)的。用大O记号一般都默认用的是该算法所有可能上界中的最下界。
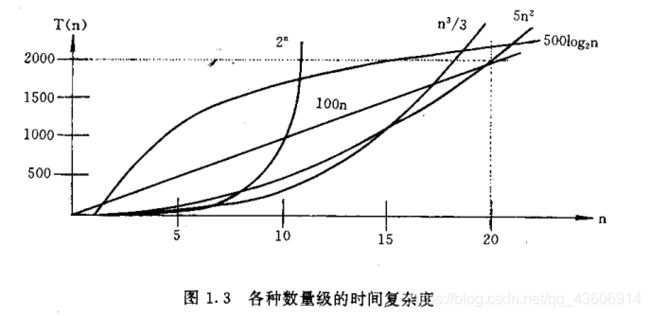
(4)常见的渐进时间复杂度比较
Ο(1)或Ο(M)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<Ο(n3)<Ο(2n)<Ο(n!)<Ο(nn)
3.同一问题不同算法的效率比较
考虑到分析算法复杂性的目的在于比较求解同一个问题的不同算法的效率,而当两个算法的渐进复杂性不同阶时,就可以判断不同算法的效率。
例2.某算法的时间复杂度为O(n^2),表明该算法的( )。
A.问题规模是Ο(n^2) B.执行时间等于n^2 C.执行时间与n^2 成正比 D.问题规模与n^2 成正比
2.C
时间复杂度为O(n^2),说明算法的执行时间T(n)<=c * n^2(c为比例常数),即T(n)=O(n^2),时间复杂度T(n)是问题规模n的函数,其问题规模仍然是n而不是n^2。
例3.下面说法中,错误的是()
Ⅰ.算法原地工作的含义是指不需要任何额外的辅助空间
Ⅱ.在相同规模n下,复杂度为Ο(n)的算法在时间上总是优于复杂度为Ο(2n)
的算法
Ⅲ.所谓时间复杂度,是指最坏情况下估算算法执行时间的一个上界
Ⅳ.同一个算法,实现语言的级别越高,执行效率越低
A.I B.I,Ⅱ C.I,Ⅳ D.Ⅲ
3.A
I 算法原地工作是指算法所需的辅助空间为常量,即O(1)
Ⅱ参见复杂度的比较
Ⅲ一般总是考虑在最坏情况下的时间复杂度,以保证算法的运行时间不会比它更长
Ⅳ这个是否正确饱有争议。王道上认为是正确的,这也是严蔚敏教材原话。不过天勤上认为这句话是错误的,解释的是大多数情况是这样,取决于编译链接后最终的机器指令,同时使用不同的编译环境情况也可能不同。也有人举例说汇编语言的执行效率比高级语言执行的效率高,因为高级语言的一条语句,可能是汇编语言的多条语句构成,包含了某些多余的语句,所以执行效率相对较低。个人更倾向于这种解释。
4.复杂度计算【部分参考王道总结】
(1)循环主体中的变量参与循环条件的判断
解答思路:设执行次数为T(n),T(n)与主体语句的变量值有关。
例4.以下算法的时间复杂度为( )。
void fun(int n) {
int i=l;
while(i<=n) i=i*2;
}
A.O(n) B. O(n2) C. O(nlog2n) D. O(log2n)
4.D
基本运算是i=i*2,设其执行次数为T(n),第T(n)次执行后i的值为2T(n)则2T(n)<=n,即T(n)<=log2n=O(log2n)。
例5.设n是描述问题规模的非负整数,下面的程序片段的时间复杂度为()。
x=2;
while(x=(x+1)*(x+1))
x=x+1;
A. O(logn) B. O(n^1/2) C. O(n) D. O(n^2)
6.B
基本运算是x=x+1,设其执行次数为T(n),第T(n)次执行后x的值为T(n)
则(T(n)+1)*(T(n)+1)<=n,即T(n)<=n^1/2-1 =O(n^1/2)。
例7.有以下算法,其时间复杂度为()。
void fun(int n){
int i=0;
while(i*i*i<=n)
i++;
}
答案为O(n^1/3) 解析同上
(2)循环主体中的变量与循环条件无关
解答思路:此类题可采用数学归纳法或直接累计循环次数。多层循环时从内到外分析,忽略单步语句,条件判断语句;只关注主体语句的执行次数。此类问题又可分为递归程序和非递归程序,嵌套循环程序:
-
非递归
例8.下列函数的时间复杂度为( )。 int func(int n){ int i=0,sum=0; while(sum -
递归
例9.【2012统考真题】求整数n(n>=0)的阶乘的算法如下, 共时间复杂度是()。 int fact(int n){ if(n<=1) return 1; return n*fact(n-1); } A. O(log2n) B. O(n) C. O(nlog2n) D. O(n^2) 递归程序一般用公式递推 T(n)=1+T(n-1)=1+1+T(n-2)=…=n-1+T(1) 即T(n)=O(n) 每次递归调用时fact()的参数减1,递归出口为fact(1),一 共执行n次递归调用。
扩展:稍微复杂的递归方程,如 T(n)=2T(n/2)+n^2
迭代法:迭代的展开方程的右边,直到没有可以迭代的项为止,这时通过对右边的和进行估算来估计方程的解。比较适用于分治问题的求解,给出其递归方程的一般形式:
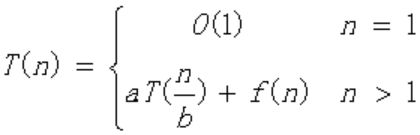
迭代过程:

直到n/2^(i+1)=1时,递归过程结束
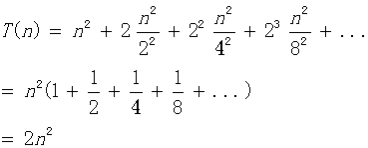
可知复杂度为O(n^2)
(3)嵌套循环
第一种情况:内层循环条件与外层循环的变量无关
例10 下列程序段的时间复杂度为()。
count=0;
for(k=1;k<=n;k*=2)
for(j=1;j<=n;j++)
count++;
A. O(log2n) B. O(n) C. O(nlog2n) D. O(n^2)
10.C
内层循环条件j≤n与外层循环的变量无关,各自独立,每执行一次j自增1,每次内层循环执行n次。外层循环条件k≤n,增量定义为k*=2,可知循环次数t满足k=2i≤n,即t≤log2n,即内层循环的时间复杂度为O(n),外层循环的时间复杂度为O(log2n)。对于嵌套循环,根据乘法规则可知,该段程序的时间复杂度O(nlog2n)。
例11.
求出其时间复杂度
for(i=0;i第二种情况: 内层循环条件与外层循环的变量有关
例12. 以下算法中加下划线的语句的执行次数为()
int m=0,i,j;
for(i=1;i<=n;i++)
for(j=1;j<=2*i;j++)
m++;
A.n(n+1) B.n C.n+1 D.n^2
- A.连加 内层循环条件j<=2*i与外层循环的变量i有关
例13
for(i=1;i<=n;i++)
for(j=1;i<=j;j++)
for(k=1;k<=j;k++)
x++;
答案是O(n^3)
例14程序段如下
for(i=n-1;i>1;i--)
for(j=1;jA[j+1])
A[j]与A[j+1]对换
其中n为正整数,则最后一行语句的频度在最坏情况下是()。
A. O(n) B. O(nlogn) C. O(n^3) D. O(n^2)