Java排序算法03:归并排序法、基数排序法、推排序法、思路分析、代码实现
文章目录
-
- 5、归并排序法
- 6、基数排序法
- 7、堆排序法 (不稳定)
5、归并排序法
归并排序是利用归并的思想实现的排序方法。如上图。思路比较简单,就是对数组进行不断的分割,分割到只剩一个元素,然后,再两两合并起来。
归并排序的时间复杂度是比较低的。
归并与快速排序法的平均时间复杂度一致,但是比快速排序法稳定。
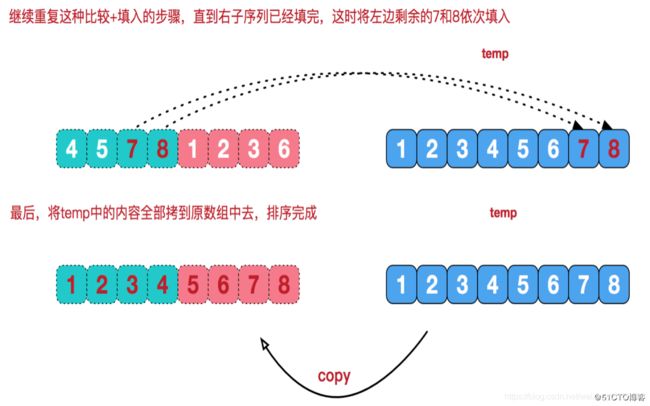
示意图:
这里展示将4578和1236合并在一起进行排序的过程:
public class MergeSorting {
public static void main(String[] args) {
int arr[] = {
3,9,-1,10,20,6};
int temp[] = new int[arr.length];
System.out.println("排序前:"+ Arrays.toString(arr));
sort(arr,0,arr.length-1,temp);
System.out.println("排序后:"+Arrays.toString(arr));
}
/**
* 拆分后合并操作
* @param arr 原数组
* @param left 原数组的左索引
* @param right 原数组的右索引
* @param temp 临时数组
*/
public static void sort(int[] arr, int left, int right, int[] temp){
// 如果左索引小于右索引 就继续拆分,先左拆分,拆分到不能拆分为止,
// 再右拆分到不能拆分为止,最后将最后拆分的结果合并
if (left < right){
int mid = (left+right)/2;
// 往左拆分
sort(arr, left, mid, temp);
// 往右拆分
sort(arr, mid+1, right, temp);
// 合并
merge(arr, left, mid, right, temp);
}
}
/**
* 合并操作
* @param arr 分割的原数组
* @param left 最左边的索引
* @param mid 中间索引
* @param right 最右边的索引
* @param temp 临时存储的数组
*/
public static void merge(int[] arr, int left, int mid, int right, int[] temp){
int i = left; // 从最左边开始的索引
int j = mid+1; // 从中间索引的下一个索引开始的索引
int t = 0; // 临时数组的起始索引
while ( i <= mid && j <= right){
// 左右两部分进行比较,小的往临时数组里放
if (arr[i] <= arr[j]){
temp[t] = arr[i];
t++;
i++;
}else {
temp[t] = arr[j];
j++;
t++;
}
}
// 总有一边的数据先放完,另一边的数据就一次放到临时数组
while (i <= mid){
temp[t] = arr[i];
t++;
i++;
}
while (j <= right){
temp[t] = arr[j];
t++;
j++;
}
// 组后将临时数组的数据全部拷贝到原数组对应位置
t = 0;
int tempLeft = left; // 原数组拆分后的起始索引位置
while (tempLeft <= right){
arr[tempLeft] = temp[t];
tempLeft++;
t++;
}
}
}
结果:
排序前:[3, 9, -1, 10, 20, 6]
排序后:[-1, 3, 6, 9, 10, 20]
6、基数排序法
占用内存很大。
基数排序法,只支持正数如果需要排序负数和正数混合的数组,就得将正数和负数分出来,到各自的数组然后对各自的数组进行装桶即可。负数判断与正数刚好相反
public class RadixSorting {
public static void main(String[] args) {
int arr[] = {
3,9,1,10,20,6};
System.out.println("排序前:"+ Arrays.toString(arr));
sort(arr);
System.out.println("排序后:"+Arrays.toString(arr));
}
public static void sort(int[] arr){
// 桶,第一个索引记录是第几个桶,第二个索引记录桶中存放的值
// 每个桶的大小都是arr.length,而不是每个桶都有数据,所以消耗空间内存
int bucket[][] = new int[10][arr.length];
// 这个数组用于记录每个桶中的元素个数
int bucketElementsCount[] = new int[10];
// 获取数组中最大的数,计算有多少位
int max = arr[0];
for (int i : arr) {
if (i>max){
max = i;
}
}
int digit = (max+"").length();
// 最大数的位数,决定了基数排序要轮回多少次,即digit-1次
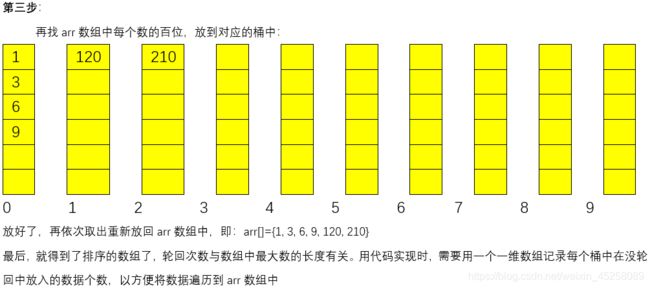
for (int i = 0; i < digit; i++) {
// 每一轮的基数都有变化,第一轮为个位,第二轮位十位,第三轮为百位,以此类推
for (int j = 0; j < arr.length; j++) {
int bucketNumber = arr[j] / (int)Math.pow(10,i) % 10;
// 将数装到bucketNumber的桶中索引为bucketElementsCount[bucketNumber]的位置
bucket[bucketNumber][bucketElementsCount[bucketNumber]] = arr[j];
// 自增,桶中的元素在增加
bucketElementsCount[bucketNumber]++;
}
// 每个数都到了自己对应的桶中之后,需要将桶中的数据都重新填到arr中
int index = 0;
for (int c = 0; c < bucketElementsCount.length; c++) {
// 如果不等于0,所以记录的该桶中是有数据的
if (bucketElementsCount[c] != 0){
for (int k = 0; k < bucketElementsCount[c]; k++) {
arr[index++] = bucket[c][k];
}
}
}
// 重置记录桶中元素的个数为0,为下一次记录做准备
for (int j = 0; j < bucketElementsCount.length; j++) {
bucketElementsCount[j] = 0;
}
}
}
}
结果:
排序前:[3, 9, 1, 10, 20, 6]
排序后:[1, 3, 6, 9, 10, 20]
7、堆排序法 (不稳定)
时间复杂度O(nlogn)
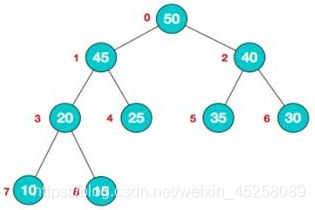
大顶堆和小顶堆,顺序存储二叉树一定是完全二叉树
- 大顶堆
顺序存储到数组(二叉树的顺序存储):
arr[]={50,45,40,20,25,35,30,10,15}
- 小顶堆
顺序存储到数组(二叉树的顺序存储):
arr[]={10,20,15,25,50,30,40,35,45}
n为父节点的索引:
左子节点是:2*n+1
右子节点是:2*n+2
n为子节点的索引,父节点为:(n-1)/2
一般升序采用大顶堆,降序采用小顶堆。
思路分析:
根据代码,画图理解
- 将待排序的序列构建成大顶堆:从最后一个非叶子节点开始调整(arr.length/2-1)。从左至右,从下至上的顺序进行调整。
- 此时,整个序列的最大值就是堆顶的根节点
- 将其与末尾元素进行交换,此时末尾就为最大值
- 然后将剩余n-1个元素重新构造成一个堆,这样在堆顶的就是次小值。如此反复执行,便能得到一个有序序列
public class HeapSorting {
public static void main(String[] args) {
int arr[] = {
4,6,8,5,9};
System.out.println("通过堆排序得到升序:");
heapSort(arr);
}
// 核心部分,这里是大顶堆的构造,升序
// 需要小顶堆,只需要将16行和21行的比较符号更改以下即可,降序
public static void adjustHeap(int[] arr, int i, int length){
int temp = arr[i]; // 记录非叶子节点(父节点)
// j为非叶子节点的左子节点
for (int j = 2*i+1; j < length; j = j*2+1) {
// 如果有右子节点并且左子节点小于右子节点,将j指向右子节点
// 否子依旧指向左子节点
if (j+1<length && arr[j]<arr[j+1]){
j++;
}
// 如果右子节点(左子节点)大于父节点,那么就将子节点赋值给父节点的位置
// 并将父节点的i指向当前节点,目的为了下一次比较以及值得交换
if (arr[j] > temp){
arr[i] = arr[j];
i=j;
}else {
break;
}
}
// 此时的i已经指向了当前节点,即将当前节点赋值为原先的父节点
arr[i] = temp;
}
public static void heapSort(int[] arr){
int temp;
// 从最后一个非叶子节点开始依次往后遍历,创建一个大顶堆
for (int i = arr.length/2-1; i >= 0 ; i--) {
adjustHeap(arr, i, arr.length);
}
// 大顶堆创建完了,就开始排序了
for (int j = arr.length-1; j >=0 ; j--) {
// 交换,因为每次大顶堆调整完之后,最大的数都在根节点,
// 因此需要将最大的数放在数组的后面,进行交换
temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
// 交换完之后,大顶堆被打乱,因此有需要调整成为大顶堆
// 因为每次交换都是讲0索引的值与当前数组最后一个值进行交换,
// 被打乱的是索引为0的根节点,所以就从根节点开始调整,长度变成了j
adjustHeap(arr, 0, j);
}
System.out.println(Arrays.toString(arr));
}
}
结果:
通过堆排序得到升序:
[4, 5, 6, 8, 9]