Step 1: 检视源数据集
import numpy as np
import pandas as pd
1.1 读入数据
file=open("D:/python练习/housing.csv")
train_df=pd.read_csv(file)
1.2 检视原数据
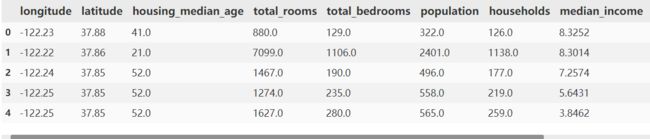
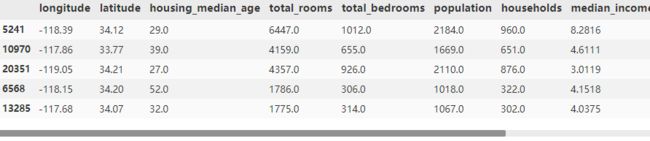
train_df.head(5)
每一行都表示一个街区。共有 10 个属性:经度、维度、房屋年龄中位数、总房间数、卧室数量、人口数、家庭数、收入中位数、房屋价值中位数、离大海距离。
train_df.info()
可以看出total_bedrooms这一项有缺失值,后面要进行处理。ocean_proximity这一项的数据类型为类别型数据。
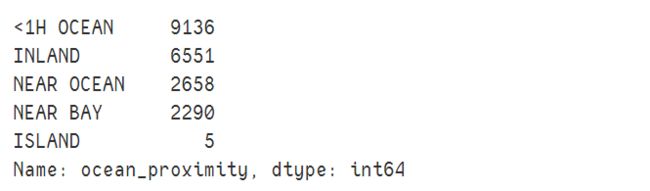
train_df.ocean_proximity.value_counts()
value_counts()方法查看都有什么类型,每个类都有多少街区
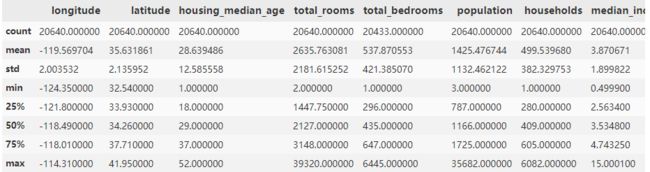
train_df.describe()
画出每个数值属性的柱状图
%matplotlib inline
from matplotlib import pyplot as plt
plt.style.use('ggplot')
train_df.hist(bins=50,figsize=(16,9))
从柱状图中可以发现以下问题:
1.这些属性的量度不一样,在后面需要进行特征缩放
2.许多柱状图的尾巴过长,对某些机器学习的算法检测规律会变得更难,所以在后面要处理成正态分布。
3.房屋年龄中位数和房屋价值中位数也被设了上限。后者可能是个严重的问题,因为它是你的目标属性(你的标签)。你的机器学习算法可能学习到价格不会超出这个界限。你需要与下游团队核实,这是否会成为问题。如果他们告诉你他们需要明确的预测值,即使超过 500000,你则有两个选项:1)对于设了上限的标签,重新收集合适的标签;2)将这些街区从训练集移除(也从测试集移除,因为若房价超出 500000,你的系统就会被差评)。
4.收入数据经过了缩放处理。
Step 2: 创建测试集
目的:防止数据透视偏差。如果一开始就看过测试集,就会不经意间按照其中的规律选择合适的算法,当再用测试集进行评估时,就会导致结果比较乐观,而实际部署时就比较差了。
from sklearn.model_selection import train_test_split
train_set,test_set=train_test_split(train_df,test_size=0.2,random_state=42)
train_test_split函数用于将矩阵随机划分为训练子集和测试子集,并返回划分好的训练集测试集样本和训练集测试集标签。test_size:如果是浮点数,在0-1之间,表示样本占比;如果是整数的话就是样本的数量。random_state:是随机数的种子。产生总是相同的洗牌指数;如果没有这个每次运行会产生不同的测试集,多次之后会得到整个数据集。
train_set.head(5)
不足之处:目前都是采用的纯随机抽样,如果数据量比较小,可能会产生偏差。所以需要关注比较重要的属性,对其进行分层抽样,比如说收入中位数。从直方图中可以看出,大多数的值在2-5(万美元),进行分层抽样时保证每一层都要有足够多的数据,这就意味着,层数不能过多。后面的代码将收入中位数除以1.5(以限制分类的数量),创建收入类别属性,用ceil对值舍入(产生离散的分类),并将大于5的分类归入到分类5。inplace=True原数组内容被改变。
train_df["income_cat"]=np.ceil(train_df.median_income/1.5)
train_df["income_cat"].where(train_df["income_cat"]<5,5.0,inplace=True)
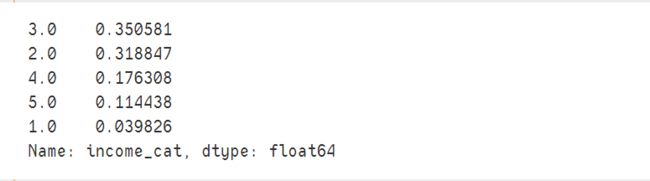
train_df["income_cat"].head(5)
train_df["income_cat"].value_counts()/len(train_df)
from sklearn.model_selection import StratifiedShuffleSplit
split=StratifiedShuffleSplit(n_splits=1,test_size=0.2,random_state=42)
for train_index,test_index in split.split(train_df,train_df["income_cat"]):
start_train_set=train_df.loc[train_index]
start_test_set=train_df.loc[test_index]
start_train_set.head(5)
for set in(start_train_set,start_test_set):
set.drop(["income_cat"],axis=1,inplace=True)
start_test_set.head(5)
需要删除income_cat属性,使数据回到初始状态。
Step 3: 数据探索及可视化
目的:以上只是粗略的查看了统计信息,还需要从样本中发现更多的信息。如果训练集非常大,可能还需要采样一个探索集。如果比较小,可以建立一个副本。
housing=start_train_set.copy()
3.1 地理数据可视化
原因:样本中有经度和纬度,所以考虑创建散点图
housing.plot(kind="scatter",x="longitude",y="latitude",alpha=0.4,figsize=(15, 10)
)
高密度区域:湾区、洛杉矶和圣迭戈等
housing.plot(kind="scatter",x="longitude",y="latitude",alpha=0.5,
s=housing.population/50,label="population",
c=housing.median_house_value,cmap=plt.get_cmap('jet'),colorbar=True,
figsize=(15, 10))
plt.legend()
加入人口信息,用点的大小来展示(s)。加入房价信息,用颜色的深浅来表示(c),用预先定义的颜色图“jet”,范围从蓝色到红色,即低价到高价。从图中可以发现房价和位置(沿海地区)以及人口密度存在联系。
import seaborn as sns
sns.set(style = "whitegrid")#设置样式
x = housing.longitude#X轴数据
y = housing.latitude#Y轴数据
z = housing.median_income#用来调整各个点的大小s
cm = plt.get_cmap('jet')
fig,ax = plt.subplots(figsize = (15,10))
#注意s离散化的方法,因为需要通过点的大小来直观感受其所表示的数值大小
#参数是X轴数据、Y轴数据、各个点的大小、各个点的颜色
bubble = ax.scatter(x, y , s = housing.population/50, c = z, cmap = cm, linewidth = 0.5, alpha = 0.5)
ax.grid()
fig.colorbar(bubble)
ax.set_xlabel('longitude', fontsize = 15)#X轴标签
ax.set_ylabel('latitude', fontsize = 15)#Y轴标签
plt.show()
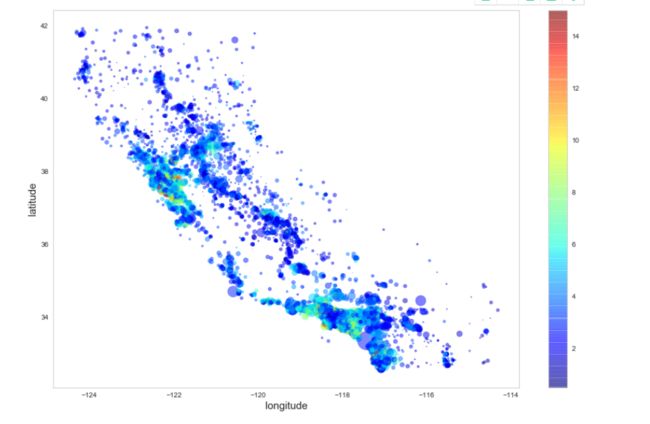
利用seaborn作图也可以达到同样效果。加入人口信息,用点的大小来展示(s)。加入收入信息,用颜色的深浅来表示(c),用预先定义的颜色图“jet”,范围从蓝色到红色,即低价到高价。从图中可以发现收入和位置(沿海地区)以及人口密度存在一定的联系,但是效果不是十分明显。
3.2 查看特征之间的相关性
corr_matrix=housing.corr()
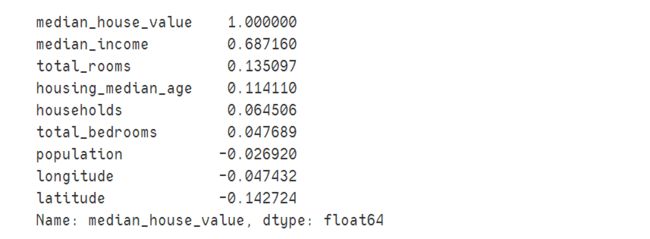
corr_matrix["median_house_value"].sort_values(ascending=False)
用热力图的方式展现相关性。annot(annotate的缩写):默认取值False;如果是True,在热力图每个方格写入数据;vmax,vmin:分别是热力图的颜色取值最大和最小范围,默认是根据data数据表里的取值确定。
import seaborn as sns
fig=plt.figure(figsize=(12,8),dpi=80)
sns.heatmap(housing.corr(),annot =True,vmin = 0, vmax = 1)
用可视化的方式展现相关性,因为属性过多,所以选取部分属性。
from pandas.tools.plotting import scatter_matrix
attributes=["median_house_value","median_income","total_rooms","housing_median_age" ]
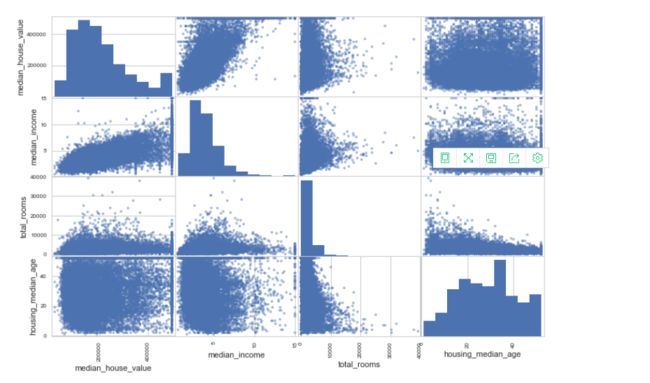
scatter_matrix(housing[attributes],figsize=(12,8))
对角线表示每个属性的柱状图。图中可以看出收入对房价的影响还是比较大的,所以可以放大进行研究。
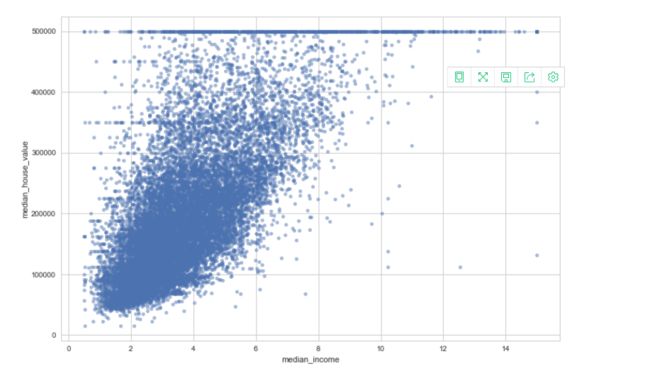
housing.plot(kind="scatter",x="median_income",y="median_house_value",alpha=0.5,figsize=(12,8))
可以看出相关性还是很高的。其次,可以看到一些直线:500000,450000,350000,280000美元,可能是收集资料时设立的边界。
3.3 属性组合试验
有一些属性,比如总房间数,在不知道街区有多少户的情况下用处不大。同理总卧室数和总人口数。
housing["rooms_per_household"]=housing.total_rooms/housing.households
housing["bedrooms_per_room"]=housing.total_bedrooms/housing.total_rooms
housing["population_per_household"]=housing.population/housing.households
corr_matrix =housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
间数和卧室数更有信息。而且每户的房间数越多,意味着房屋更大,房价越高,比单纯的看总房间数更有信息。
Step 4: 数据预处理
目的:为机器学习算法准备数据。
housing=start_train_set.drop("median_house_value",axis=1)
housing_copy=housing.copy()
housing_labels=start_train_set.median_house_value.copy()
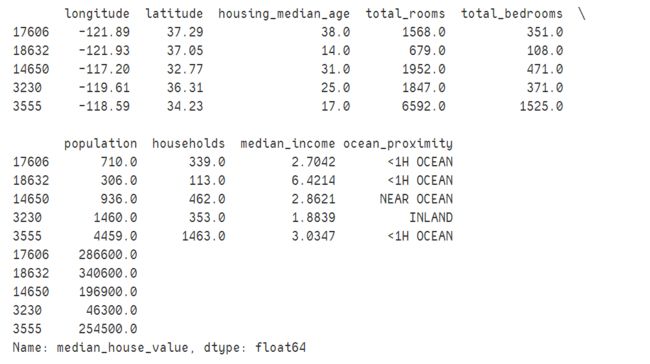
print(housing.head(5))
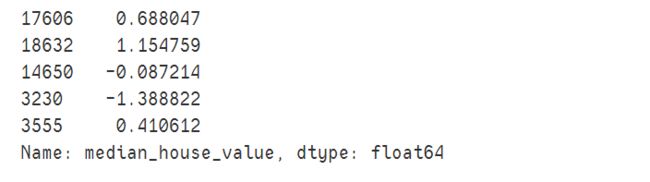
print(housing_labels.head(5))
将训练集中预测量和标签分开,因为之后对其要进行不同的转换;drop()创建备份,不影响原数据集。
4.1 数据清洗
目的:处理缺省值。因为很多机器学习算法对缺省值比较敏感(例如LR和SVM,决策树和朴素贝叶斯相对好一点)
思路:1)去掉缺失的行数据dropna();2)去掉缺失的列drop();3)进行赋值fillna(),可以是0、平均数和中位数。
median=housing.total_bedrooms.median()
housing.total_bedrooms=housing.total_bedrooms.fillna(median)
housing.isnull().sum().sum()
4.2 处理文本和类别属性
housing=pd.get_dummies(housing)
housing.head(5)
pandas自带的get_dummies方法,可以帮你一键做到One-Hot。可以看出类别属性ocean_proximity被我们分成了5个column,每一个代表一个category。是就是1,不是就是0。
4.3 特征缩放
当输入的属性量度不同时,会影响机器学习算法的性能。比如总房间数分布范围在6-39320,收入中位数在0-15。两种方法:归一化和标准化。归一化将数值缩放到0-1之间,标准化不会限定到某个范围,对一些算法有影响,像神经网络算法输入值就必须是0-1。但是异常值对标准化的影响较小。
numeric_cols=housing_copy.columns[housing_copy.dtypes!="object"]
print(numeric_cols)
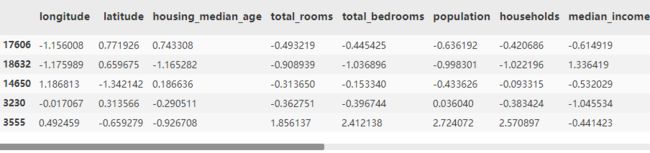
numeric_col_means = housing.loc[:, numeric_cols].mean()
numeric_col_std = housing.loc[:, numeric_cols].std()
housing.loc[:, numeric_cols] = (housing.loc[:, numeric_cols] - numeric_col_means) /numeric_col_std
housing.head()
housing_labels=(housing_labels-housing_labels.mean())/housing_labels.std()
housing_labels.head()
Step 5:模型选择和训练
5.1 在训练集上训练和评估
from sklearn.linear_model import LinearRegression
lin_reg=LinearRegression()
将DF转化为Numpy Array
X_train=housing.values
X_test=housing_labels.values
print(X_train)
print(X_test)
先训练一个线性回归模型
lin_reg.fit(X_train,X_test)
训练完成,用交叉验证法进行模型评估。交叉验证的基本思想是将训练数据集分为k份,每次用k-1份训练模型,用剩余的1份作为验证集。按顺序训练k次后,计算k次的平均误差来评价模型(改变参数后即为另一个模型)的好坏。
from sklearn.model_selection import cross_val_score
lin_reg_scores=cross_val_score(lin_reg,X_train,X_test,scoring="neg_mean_squared_error",cv=10)
lin_reg_rmse_scores=np.sqrt(-lin_reg_scores)
print(lin_reg_rmse_scores.mean())
均方根误差(RMSE),回归任务可靠的性能指标。
利用决策树模型试试看
from sklearn.tree import DecisionTreeRegressor
tree_reg=DecisionTreeRegressor()
tree_reg.fit(X_train,X_test)
tree_reg_scores=cross_val_score(tree_reg,X_train,X_test,scoring="neg_mean_squared_error",cv=10)
tree_reg_rmse_scores=np.sqrt(-tree_reg_scores)
print(tree_reg_rmse_scores.mean())
可以看出决策树模型的误差大于线性回归,性能更差一点。现在选择用随机森林尝试一下。
from sklearn.ensemble import RandomForestRegressor
RF_reg=RandomForestRegressor()
RF_reg.fit(X_train,X_test)
RF_reg_scores=cross_val_score(RF_reg,X_train,X_test,scoring="neg_mean_squared_error",cv=10)
RF_reg_rmse_scores=np.sqrt(-RF_reg_scores)
print(RF_reg_rmse_scores.mean())
随机森林速度慢一点,误差更小,明显更有希望。
5.2 利用网格搜索对模型进行微调
只要提供超参数和试验的值,网格搜索就可以使用交叉验证试验所有可能超参数值的组合。
from sklearn.model_selection import GridSearchCV
param_grid = [
{'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},
{'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},
]
forest_reg = RandomForestRegressor()
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,
scoring='neg_mean_squared_error')
grid_search.fit(X_train,X_test)
首先调第一行的参数为n_estimators和max_features,即有34=12种组合,然后再调第二行的参数,即23=6种组合,具体参数的代表的意思以后再讲述。总共组合数为12+6=18种组合。每种交叉验证5次,即18*5=90次模型计算,虽然运算量比较大,但运行完后能得到较好的参数
grid_search.best_params_
可以看到最好参数中30是选定参数的边缘,所以可以再选更大的数试验,可能会得到更好的模型,还可以在8附近选定参数,也可能会得到更好的模型。
grid_search.best_estimator_
得到最佳的估计器
5.3 用测试集去评估系统
from sklearn.metrics import mean_squared_error
final_model = grid_search.best_estimator_
X_test = start_test_set.drop("median_house_value", axis=1)
y_test = start_test_set["median_house_value"].copy()
median=X_test.total_bedrooms.median()
X_test.total_bedrooms=X_test.total_bedrooms.fillna(median)
X_test=pd.get_dummies(X_test)
numeric_col_means = X_test.loc[:, numeric_cols].mean()
numeric_col_std = X_test.loc[:, numeric_cols].std()
X_test.loc[:, numeric_cols] = (X_test.loc[:, numeric_cols] - numeric_col_means) /numeric_col_std
y_test=(y_test-y_test.mean())/y_test.std()
final_predictions = final_model.predict(X_test)
final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
print(final_rmse)
把测试集进行预处理,导入到系统中,误差为0.462982088615,模型的表现还不错。