【毕设论文】基于pix2pix的数据增强方法在工业芯片表面缺陷检测中的应用（合肥工业大学2021届物联网工程毕业论文）

  论文的tex源码已经上传到GitHub了。

基于pix2pix的数据增强方法在工业芯片表面缺陷检测中的应用
Application of data enhancement method based on pix2pix in Surface Defect Detection of Industrial Chips

摘要

  工业芯片被广泛应用于各个领域，种类繁多，效用良好、效益非凡，同经济社会的发展紧密不可分割，对于第四次工业革命与新型基础建设不可或缺。因此，工业芯片的设计制造受到广泛关注，而工业芯片检测是其生产工序的关键步骤，芯片检测达标与否直接决定该芯片能否出厂。基于深度学习的目标检测技术推陈出新，检测精度与速度不断提高，其检测的高精度与实时性符合大规模工业环境下芯片检测的需求故而被企业采用。深度学习目标检测算法对数据的依赖性极大，只有高质量、大规模的数据才能使模型得到充分训练，而获取工业芯片样本的代价较为可观。

  为了解决芯片检测算法数据依赖性和工业芯片样本获取困难之间的冲突，本文尝试使用原始的缺陷芯片图像数据集，基于生成对抗网络GAN生成一定数量与原数据集同分布的缺陷芯片图像，将之用于扩增原始数据集以达到提高缺陷检测算法精度的目的。具体内容如下：

  1）提出了一种基于Pix2Pix GAN的可用于生成指定坐标与面积的芯片缺陷的方法。该方法根据已有芯片缺陷的标注，在正常芯片对应区域涂抹白斑作为mask，将mask图像与缺陷图像一同输入Pix2Pix GAN进行训练。实验表明，该方法生成的工业缺陷芯片图像与目标图像具有较高的逼真度，缺陷区域的拟合性较好，用于缺陷检测器的数据增强可提高检测精度。

  2）针对Pix2Pix GAN生成图像的缺陷区域不够真实的问题，本文提出一种芯片缺陷生成对抗网络（Chip Defect Synthesis-GAN，CDS-GAN）。该模型使用深度残差网络作为生成器的骨干架构，并添加自注意力机制引导专注缺陷区域的合成，判别器采用两个不同尺度的感受野对生成-真实缺陷图像对进行判别；为了提高生成图像与目标图像在人眼视觉上的相似度，使用感知损失减小两者高级语义特征的差异；此外，引入WGAN-GP梯度惩罚函数对判别器的更新进行约束，使模型训练稳定并趋于收敛。实验结果表明，本文模型较之Pix2Pix GAN以及其他变种GANs所生成的工业芯片图像质量更高、多样性更丰富，并且具有良好的鲁棒性与泛化性，可用于其他类型的工业表面缺陷图像，另外本文模型在公开数据集的图像翻译任务上优于Pix2Pix GAN。本文模型生成图像提升SSD缺陷检测器精度的效果优于Pix2Pix GAN。

关键词：


深度学习；生成对抗网络；数据增强；缺陷检测

ABSTRACT

  Industrial chips are widely used in various fields, with miscellaneous types, good utility and remarkable benefits. They are closely inseparable from the development of economy and society and are indispensable for the 4th industrial revolution and new infrastructure construction. Therefore, the design and manufacture of industrial chips are widely concerned as the industrial chip detection is the crucial step in the production process. Whether the chip detection meets the standard directly determines whether it can be delivered. The object detection technology based on deep learning is bringing forth the new through the old and the detection accuracy and speed are constantly improved. The high precision and real-time performance of the detection satisfy the demands of chip detection in large-scale industrial environment, therefore, it has been adopted by enterprises. The deep learning object detection algorithm has a great dependence on data that only high-quality and large-scale data can the model be fully trained while the cost of obtaining industrial chip samples is considerable.

  In order to solve the conflict between the data dependence of chip detection algorithm and the difficulty of obtaining industrial chip samples, this thesis attempts to use the original defect chip image data set to generate a certain number of defect chip images distributed with the primitive data set based on the Generative Adversarial Networks, which is used to expand the initial data set to improve the accuracy of the defect detection algorithm. The details are as follows:

  i) A method based on Pix2Pix GAN is proposed to produce chip defects with specified coordinates and area. According to the existing chip defect labeling, white spots are smeared on the corresponding area of the normal chip as mask, and then the mask image and defect image are input into Pix2Pix GAN for training. The experimental results show that the industrial defect chip image generated by this method has high fidelity with the target image and the fitting of the defect area is good. The detection accuracy can be improved when it is used to enhance the data of the defect detector.

  ii) Aiming at the problem that the defect area of images produced by Pix2Pix GAN are not real enough, this thesis proposes a chip defect synthesis GAN (CDS-GAN). In this model, the deep residual network is used as the backbone of the generator, moreover, the self-attention mechanism is added to guide the synthesis of focused defect regions. The discriminator uses two receptive fields of different scales to discriminate the generated and real defect image pairs; In order to improve the visual similarity between the generated image and the target image, the perceptual loss is used to reduce the difference between the two high-level semantic features; In addition, WGAN-GP gradient penalty function is introduced to constrain the update of the discriminator, so that the training of the model is stable and tends to converge. Experimental results present that compared with Pix2Pix GAN and other variants of GANs, the image quality generated by the proposed model is higher, the diversity is richer and it has good robustness and generalization, which can be used for other types of industrial surface defect images. Furthermore, the proposed model is superior to Pix2Pix GAN in image translation task of public data set. The results find that the model can improve the accuracy of SSD better than Pix2Pix GAN.

KEYWORDS:

Deep Learning; Generative Adversarial Networks; Data Augmentation; Defect Detection

绪论

选题背景与意义

  芯片是现代大规模集成电路的产物，因其具有功能强、精度高、体积小、功耗低与可扩展等特点，而被广泛用于各个领域，如计算机领域、互联网领域、电子通信领域、现代电子设备领域、航天航空领域、载具开发领域、国家高新科技开发领域，等等。芯片可谓与人们的日常生活息息相关，已经深入到社会生产生活、科研活动、国防建设的方方面面，并且这种关联还有持续增强的趋势[1, 2]。

  正因为芯片是一种关乎国计民生的重要产品，因此它的制作工艺与流程备受关注。在当前的工业体系中，芯片还无法达到一步到位的单一化生产模式，其制程包含若干阶段和若干流程，芯片的生产流程如图1.1所示。在经过一系列制程步骤得到芯片产品后，因为完整的芯片在其繁杂的制备流程的任一阶段都可能被破坏、污染，从而产生缺陷，无法直接投入使用，仍需要进行抽样检测。芯片的表面缺陷在导致其损毁无法使用的因素中占了很大比重，因此快速、准确地检测出芯片样品中含表面缺陷的所有芯片，对于芯片制作厂商具有巨大的意义。

  基于深度学习方法被发现较之传统的检测方法，对于工业表面缺陷检测更加优越，无论是缺陷检测的准确率、检测速率、覆盖率都得到了显著提升[3]。为此，大量基于深度学习的目标检测算法被用于工业缺陷表面检测的场景[4, 5, 6, 7, 8, 9, 10]。

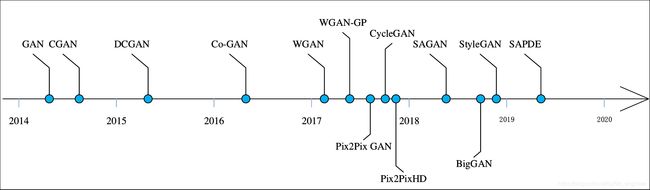
  深度学习是机器学习的一种实现方式，后者是人工智能技术的一个重要分支。深度学习作为表现最为优越的机器学习算法，目前已经俨然成为人工智能领域研究的主流。目标检测算法作为深度学习中最为活跃的研究方向之一，自提出伊始就得到了学界与工业界的大量关注，近年来更是发展迅猛。多数具有代表性的目标检测算法均从多个方面尝试改进网络深度学习网络架构，按照检测步骤可以分为基于回归的one-stage框架和基于候选框的two-stage框架[11]。two-stage算法分为两个阶段，预先选取一系列候选框，再对候选框进行定位分类。one-stage算法采用回归的方法通过单一的CNN网络，直接获取图像中的目标位置与类别。当下流行的目标检测算法提出的时间，如图1.2所示。

  值得一提的是，基于深度学习的目标检测网络结构一般都层数较深、参数量庞大，其性能极大地依赖于训练数据的质量和数量。有鉴于此，包含大量自然场景的数据集被设计出来，如在PASCAL
VOC挑战赛中被广泛使用而得名同名数据集VOC，Microsoft公司建立的MSCOCO数据集，美国斯坦福大学贡献的ImageNet数据集，还有其他包含生物特征、姿态形体、生物医药数据的数据集，作为公开的基准数据用于验证深度学习目标检测算法。这些公开数据集在一定程度上促进了深度学习目标检测算法的发展，同时，其又因此而得以不断完善补全。

  本文的研究课题来自企业项目，合作企业专注基于机器视觉的半导体封装检测产品研发。基于深度学习的算法往往都需要在大量数据集上进行多次训练才能得到理想的效果。然而，对含有表面缺陷的芯片进行人工标注依赖专家完成，代价高昂、获取周期长、困难较大，且采样的训练样本必然不可能包含所有缺陷特征。与此同时，标注数据的高质量和多样性对于基于深度学习的目标检测算法更不可或缺。不论是标注数据质量低或多样性不足，都会造成芯片目标检测网络过拟合等负面效果。过拟合是指模型过甚拟合了训练集的数据分布，在训练集上表现良好，但在交叉测试集上性能表现不充分，泛化能力差，具体对芯片目标检测来说，即在训练集上损失函数值很小，但在测试集上损失函数值很大。标注样本过少是造成过拟合的主要原因之一[12]。自然地，可知解决这个问题的手段之一即是针对芯片图像数据进行增强，从而获取更多特征的训练样本，进而提高目标检测算法的检测精度，该工作对于提供工业缺陷检测效率、降低人工采样成本意义重大。

  当前的数据增强方法已经较为成熟，然而流行的数据增强工作主要集中于自然图像领域，在工业表面缺陷，尤其是芯片表面缺陷上的研究缺乏代表性的成果。故而在芯片表面缺陷数据上的数据增强仍有待进一步研究。Goodfellow[13]等于2014年基于"零和博弈"思想提出来的生成对抗网络（Generative Adversarial Network，GAN）是一种有望解决该问题的理想工具，它可以通过学习目标样本的数据分布，生成大量与原始样本独立同分布的数据样本，而这正好契合了数据增强的初衷。受此启发，本文的目的是将GAN应用于芯片表面缺陷数据增强，设计一种适用于芯片图像增强且具有一定普适性和通用性的网络模型，并对其性能表现进行验证，使之有助于解决芯片表面缺陷检测中正负样本极度失衡问题带来的模型过拟合。GAN的基本结构如图1.3所示。

研究现状

  因本文的研究主题是使用生成对抗网络GAN给工业表面缺陷（本文以芯片为例）这一任务做数据增强，故该部分内容的介绍本文分为两个板块来讲述国内外研究现状与发展趋势。首先，本文将介绍近年来国内外所提出的GAN的代表性工作；其次，描述基于GAN对工业表面缺陷数据进行数据增强的研究动向。本文将分析这些典型网络的优缺点，以及本文的研究如何规避GAN中的问题，并借其完成工业芯片表面缺陷数据增强的工作。

生成对抗网络GAN的研究进展

  至今，学界对GAN的研究余热未消，近年来的CVPR[14, 15]、ICCV[16, 17]、NIPS[18, 19]、ACM MM[20, 21]等会议以及TPAMI[22, 23]、IJCV[24, 25]、IEEE TIP[26, 26]等刊物每年都会收录若干关于GAN的研究论文，因此可以判定，GAN自今后一段时间仍将是计算机视觉领域关注的焦点话题。也正由于该因素，GAN的变种网络及其研究应用，自2014伊始就接连被学者提出。较为典型的GANs各自提出时间，如图1.4所示，下面将对其中的几种进行介绍。

  1）条件生成对抗网络CGAN

  原始GAN虽然能够生成与原始数据同分布的样本，但生成数据模式不受控，无法满足研究人员的需要，且极易引发模式崩溃（model collapse）。为了解决这一问题，Mirza等[28]于2014年，即原始生成对抗网络GAN发表的同期提出了条件式生成对抗网络（Conditional Generative Adversarial Network，CGAN）。CGAN是在GAN的基础上引入约束条件，亦即在生成器（Generator）和判别器（Discriminator）中添加各一个条件变量$y$，$y$的选择具有宽泛性。条件变量$y$的加入使模型的有效增益得到了加强，训练过程因$y$的约束可控性有所增加，正因如此有学者将CGAN归入有监督学习的范畴[29]。CGAN的基本结构如图1.5所示。

  CGAN通过在网络结构中引入约束变量$y$，使之可借辅助信息进行模型训练，显著提升了生成样本的质量。然而，由于约束变量$y$所提供的外部信息单一化，难以彻底解决GAN生成样本可控性低的问题。但值得一提的是，CGAN为后续GAN的改进工作明确了可行方向，即将约束条件应用到GAN中，可以帮助解决其生成样本质量差、多样性不足的问题。

  2）深度卷积生成对抗网络DCGAN

  卷积神经网络（Convolutional Neural Network，CNN）[30]是深度学习领域划时代的产物，诞生以来就备受学界推崇[31, 32, 33)]。深度卷积生成对抗网络DCGAN[34]首次将卷积神经网络CNN引入GAN中，利用CNN强大的特征提取能力来增益GAN的模型性能。为了加快收敛速度、提升生成样本质量，并支持更多元化的真实数据，如高分辨率的图像作为输入[35]，DCGAN对原始GAN的生成器和判别器进行了修改。DCGAN生成器的基本结构如图1.6所示。

  由于采用了CNN结构，DCGAN提取图像特征的能力得到了极大提高，因而在图像处理领域得到了广泛应用。但是，DCGAN中的多层神经卷积网络会造成生成图像的棋盘状纹理，即使采用了批归一化、卷积核大小整除步长等技巧仍无法完全消除，而层数过少的神经卷积网络无法充分提取图像特征，两者难以平衡。

  3）WGAN与WGAN-GP

  GAN极具启发性与开创性，功能也非常强大，但其本身仍具有收敛速度慢、难以训练（训练不稳定）、生成样本多样性单一等弊端。对于原始GAN所存在的问题，许多研究者提出了不同的解决方法，有的是专注于某一特定场景的具体应用，而有的则尝试分析原始GAN的问题所在，给出针对性的改进方案。大多数研究都无法从根本上解决GAN产生的收敛速度慢、训练不稳定、生成样本单一、模式崩溃等问题，而WGAN（Wasserstein GAN）成功地做到了这一点。

  Martin Arjovsky等[36]设计了所谓的Wasserstein距离用以取代原始GAN中的JS散度作为惩罚函数，得到了一种可以稳定训练的生成对抗网络WGAN。Tim Salimans[37]等在WGAN中增添梯度惩罚项GP，提出了WGAN的改进版WGAN-GP，其比WGAN收敛得更快，生成样本的质量也更高。

  理论上，WGAN-GP拥有比WGAN更快的收敛速度、生成样本的质量也愈高，实验结论一般与此相符合，WGAN-GP往往比WGAN更易于训练。

  4）CycleGAN

  CycleGAN（Cycle-Consistent Generative Adversarial Network，循环一致性生成对抗网络）[38]是一种基于对偶学习的GAN网络模型，其不需要成对的训练数据就可实现源域数据到目标域数据的风格转换。所谓风格转换就是将一种风格的图像转变成为另一种不同风格的图像[39]，如将W风格的画作转换为M风格的画作，如图1.7所示，CycleGAN并不要求转换中的W与M具有一一对应的关系。

  CycleGAN先学习从源域数据到目标域数据的映射，再完成从目标域数据到源域数据的逆转映射，利用对偶学习的思想消除了训练数据配对的限制。CycleGAN的基本结构如图1.8所示。

  CycleGAN最出色的贡献在于将对偶学习与GAN进行成功结合，训练时不要求源域数据与目标域数据相互配对，可以胜任许多成对数据获取困难的场景，同时在图像风格转换方面取得了巨大的成功，但是CycleGAN仍然存在不足与值得改进之处。

  首先CycleGAN的生成器采用的是原始GAN的生成对抗损失函数，即使有循环一致性损失的约束，依然无法完全规避生成样本质量低、多样性差，且难以稳定训练，会发生模式崩溃的情况。CycleGAN在图像风格转换上的成功是有目共睹的，但这仅限于对图像的纹理与色彩进行转换，当图像的目标区域与背景差别较小（如灰度图）时，难以胜任图像转换任务，另外，CycleGAN对几何形状分明物体图像转换效果不理想[37]。

  5）Pix2Pix GAN

  Pix2Pix[39]是一个通用的图像翻译（Image Translation）网络，其可以看作是CGAN的延伸。Pix2Pix完成的任务也是将源域图像转换为目标域图像，类似于将一种语言翻译为另一种语言，故也被称作"图像翻译"。Pix2Pix采用了CGAN对模型添加约束变量的思想，但由于Pix2Pix的应用场景要求输入是配对的图像，因此需对CGAN的结构进行改进。Pix2Pix的基本结构如图1.9所示。

  Pix2Pix较之CycleGAN的明显短板就是前者需要配对的图像作为输入，而这在现实场景中并不总是成本可控的，但是Pix2Pix由于使用了CGAN的思想，将源域图像作为约束变量，在提高生成样本质量的同时，也在一定程度上使训练过程中损失函数趋于收敛。值得一提的是，Pix2Pix是一个普用的图像转换工具，且生成图像纹理清晰、色彩区分度高、几何形状轮廓显著，即使目标区域与背景差距不显仍然能够胜任工作，这恰是本文的工作场景所需；另外，Pix2Pix对于数据量的要求较低，较小的数据集也能取得令人满意的效果。

  本文的任务是完成芯片表面缺陷的图像增强工作，缺陷图像是随正常芯片一起通过高分辨率相机拍摄芯片样本获得的，数据来源固定，保证了正常图像与缺陷图像对的数量；芯片图像都经过处理转换为灰度图，缺陷与背景的区分度有所缩减。

  综上所述，本文采用Pix2Pix GAN作为基准模型，对芯片表面缺陷进行图像增强，并针对Pix2Pix GAN网络的不足做出改进。下面介绍近几年国内外基于GAN对工业表面缺陷进行数据增强的相关工作。

基于GAN的工业表面缺陷数据增强相关工作

  2014年至今，针对某些特定的工业场景，如：原始缺陷数据采集不便，采集的缺陷图像所含缺陷类别不平衡，原始缺陷样本数量过少等，而采用GAN进行工业表面缺陷图像的数据增强，生成与原始缺陷样本相似的图像，达到扩充训练数据集的目的。相关工作不断被学者探讨研究，一些实验室效果表现良好的模型被提出，有关研究成果脱胎于实验室环境，尝试面向真实的工业场景应用，本文列举了一些采用GAN实现工业表面缺陷图像增强的工作，这些工作都在不同的表面缺陷数据集上进行了有益的尝试，并在最后对GAN无法大规模工业运用的原因进行了总结分析。

  国内外学者从多个途径改进GAN使之应用于工业表面缺陷的数据增强，下面介绍这个方向的进展。

  杜虎强[40]提出了一种基于Pix2Pix的网络模型来生成含缺陷的晶元图像，该方法需针对晶元图像的特征采用某种模式识别算法筛选满足条件的晶元图像，用以作为GAN的训练数据，其生成的晶元图像与真实样本具有较高的拟合度。张晋等[41]通过将DCGAN生成器$G$的输入随机噪声$z$转换为高斯噪声，提出了用于生成含缺陷的磁瓦图像的高斯混合型DCGAN网络，该模型增益了生成小样本且具有同类特征图像的能力，使得所生成的磁瓦图像质量及其所含缺陷类别有所提高。谢源等[42]也提出了一种改进DCGAN网络来生成含表面缺陷的注塑瓶图像，针对DCGAN的判别器$D$无法有效识别缺陷区域，在判别器$D$损失函数中添加二分类损失函数用于判断图像的特定块是否含缺陷，并加入梯度惩罚函数使得训练更稳定；该模型生成的含缺陷图像对于提升分类器的准确率较为显著。刘坤等[43]针对太阳能电池的EL表面缺陷数据与正样本不平衡的问题，提出了一种NSGGAN用于生成负样本，该方法使用高斯噪声作为判别器$G$的唯一输入，并在判别器中添加负样本引导损失函数，增强对负样本的判别能力，改进WGAN的梯度惩罚函数使判别器的梯度更新适于模型在当前数据集训练时收敛；通过实验，表明该方法的改进对于太阳能电池EL表面缺陷图像的生成是有效的，所生成样本能够改善缺陷检测的精确度与召回率。Gangjie Zhang等[44]通过在生成器$G$中添加SPADE正则化机制得到缺陷的空间分布与图像特征，该操作便于使生成图像所含缺陷分布更为随机，且为了提高不同类别的缺陷将随机噪声高斯化，在判别器$D$的损失函数中添加分类损失使生成的缺陷与目标类别保持一致，另外，该模型将缺陷生成分为两个步骤：先使用SPADE正则化得到缺陷"前景"，再在正常图像的表面添加缺陷前景，即使用缺陷转移的方法来生成含表面缺陷的样本；该模型在CODEBRIM上的实验结果优于同类方法，其生成的缺陷样本具有一定的保真度与多样性。Juhua Liu等[4545]将纺织物的表面缺陷生成分为两个阶段，采用VGG提取经随机裁剪仅含缺陷的纺织物的图像特征，所得缺陷特征作为约束变量用于训练第一阶段的GAN，生成的纺织物缺陷当作前景镶嵌到另一张纺织物图像的空白裁剪区域，参与第二阶段GAN的训练，为了增强生成样本与真实图像的拟合度，该阶段的生成器$G$损失函数引入重构损失与感知损失，而最终得到含表面缺陷的纺织物图像；实验结果表面，该模型所生成的含表面缺陷的纺织物图像可提升分类器的性能。Bin Li等[46]使用$D2$[47]损失函数取代CycleGAN的判别器$D$损失函数中的对抗损失，并在CCSD-L与CCSD-NL数据集上对模型进行实验，结果表明该方法所生成的含表面缺陷样本的FID值比基准模型有小幅降低，将生成样本用于缺陷识别与分类，结果表明扩充后的数据集有正向增益。Rippel等[48]提出了一种改进CycleGAN用于纺织物表面缺陷图像的生成，其使用mask语义图像与带有表面缺陷的纺织物图像作为输入，mask以二值图像方式标记出缺陷位置，通过增加判别器patchGAN对图像不同面片（patch）的感知权值，实现缺陷位置的准确定位识别，同时，为了增加训练的稳定性，该方法将最小方差（Least Square Error，LSE）结合谱归一化（Spectral Normalization）应用于生成对抗损失；实验结果表明，该模型生成的含表明缺陷的纺织物图像质量较高，但缺陷类型单一。

  通过回顾近些年国内外学者的工作可以认识到，仅仅针对某种或某类工业表面缺陷改进现有的GAN，无法满足工业条件下多样性的数据要求，更不能解决工业表面缺陷数据正负样本不均衡所引起的识别、检测及分类等问题。当前，无法将GAN应用于工业环境的数据增强，原因可以概括如下：

  1）原始GAN只能生成如MNIST数据集和低分辨率面部灰度图的样本。工业场景一般对图像的分辨率有较高要求，或需模型可自适应输入图像的分辨率，低分辨率图像丢失了原有的纹理、色彩、轮廓等频域信息与尺寸等空域信息，所能表达的特征不足以使后续模型完成对图像的检测、识别和分割。

  2）原始GAN生成的样本特征单一。数据增强的目的之一是获得具有更为丰富特征的样本，从而提高后续模型的泛化能力，原始GAN无法提供获取多样性样本的途径，不能完美解决数据增强的任务。

本文研究内容与工作安排

本文研究内容

  芯片诞生于"第三次工业革命"，是人类智慧的结晶，芯片制造归属于集成电路产业，随着集成电路的快速发展，芯片的制造工艺也日益复杂化，每一道工序都可能在芯片表面造成缺陷。鉴于芯片表面缺陷的多样化与复杂化，人工抽检的周期长，实时性差，准确性低，并不适用于芯片的表面缺陷检测，其不符合企业生产标准。近几年，深度学习与机器视觉推陈出新，为工业表面缺陷检测提供了许多强有力的工具。然则，这些方法大都基于有监督的深度学习，需要大量带有标签的训练数据。样本采集的成本高、周期长，且所得数据包含所有缺陷样本的概率为零。

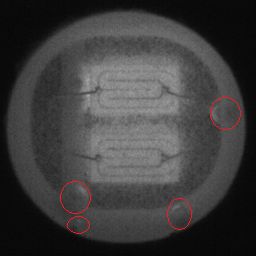
  本文针对采用深度学习方法，进行工业芯片表面缺陷检测时所面临的数据缺乏，设计一种适用于芯片表面缺陷图像生成，同时具备一定通用性与泛化性的图像增强方法，称之为CDS-GAN（Chip Defect Synthesis），来解决工业芯片表面缺陷的负样本匮乏问题。本文选取了两种类型的工业芯片数据集作验证所需，一种是应用点胶工艺制成的LED芯片，该类型芯片表面可能包含气泡、缺铜等缺陷，另一种是采用电泳法生产的GPP芯片，该类型芯片可能包含玻璃层损伤、划损等缺陷。两类芯片及其含表面缺陷，如图1.10所示。

本文工作安排

  本文共分为5个章节，全文的组织结构安排如下：

  第一章，介绍了基于生成对抗网络GAN进行工业芯片表面缺陷图像增强的研究背景与研究意义，列举了具有代表性的改进GAN网络，通过梳理文献并回顾前人采用GAN在工业表面缺陷方向的研究工作，总结分析了GAN在工业缺陷数据增强上的不足。章末阐明了本文的创新点与组织结构。

  第二章，重点阐述了GAN的基本原理及其结构性问题，而后介绍了基于Pix2Pix GAN进行芯片表面缺陷的图像增强，并指出该方法的应用具有哪些局限性。

  第三章，提出了一种基于Pix2Pix GAN的模型CDS-GAN，用于完成生成含表面缺陷芯片图像的工作，详细阐述了CDS-GAN的网络结构与优化方法。

  第四章，为了证明所提CDS-GAN的有效性和鲁棒性，在多个数据集上进行了实验，并选取恰当的GAN评价指标定量评估，与Pix2Pix、CycleGAN、DCGAN进行了对比；用CDS-GAN与Pix2Pix所生成图像，以及复制粘贴的图像分别扩增原始数据集，用于训练分类器，并选择mAP作为评价指标，对照实验结果表明CDS-GAN可用于工业表面缺陷的数据增强；通过消融实验，证明CDS-GAN各个模块的有效性。

  第五章，对Pix2Pix和本文所提CDS-GAN用于工业芯片表面缺陷的数据增强进行总结，列举了二者的优缺点并展望了未来的工作方向。

生成对抗网络GAN的原理与应用

  本文1.2.2节介绍了生成对抗网络GAN的若干改进网络，但并未详细阐述原始GAN的基本原理，下面对此进行详细论述，并介绍原始GAN的结构性问题，最后给出1.2.2节所介绍的Pix2Pix GAN，即本文的基准模型，其用于芯片表面缺陷的图像增强的示例。

GAN的基本原理

  Goodfellow等[13]基于博弈理论中"零和博弈"的思想将GAN划分为两个模块：生成器（Generator，$G$）与判别器（Discriminator，$D$），生成器$G$与判别器$D$之间不断进行对抗学习。原始GAN的基本结构，如图2.1所示。

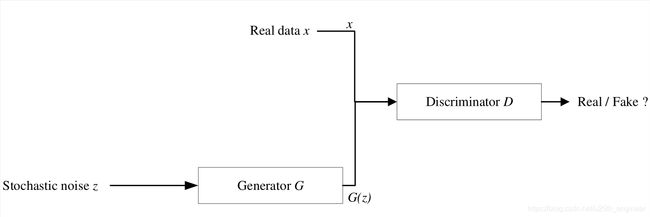
  生成器$G$的输入是服从某一先验分布$p_z(z)$的随机噪声$z$，输出是服从某一分布$p_g(x)$的高维数据$G(z)$。本文假设真实数据服从分布$p_{data}(x)$，$G$的目标是令生成数据分布$p_g(x)$与真实数据分布$p_{data}(x)$尽可能接近以欺骗$D$。与之相反，$D$的目标是准确地判断其输入数据是来自真实样本$x$还是生成样本$G(z)$，最终给出一个$[0,1]$的数值：其值与0的差距愈小，$D$认为其来自生成样本$G(z)$的概率愈大；其值为1，$D$认为其更可能来自真实样本$x$。

  为了定量评估两个分布$p_{data}(x)$与$p_g(x)$的差异，引入目标函数$V(G,D)$，如式2.1所示。

$$V(G,D)={\mathbb{E}}_{x\sim p_{data}(x)}[\log D(x)]+{\mathbb{E}}_{x\sim p_g(x)}[\log (1-D(x))]\text{\hspace{1em}(2.1)}$$

  对于GAN，直观上，若想使$p_{data}(x)$与$p_g(x)$之间距离最大，相应地$V(G,D)$也需取最大值，而因$V(G,D)$与两个数据分布相关，具体操作是：给定$G$，寻找$D^{\ast }$使$V(G,D)$最大，即：

$$D^{\ast }=\arg \underset{D}{\max }V(G,D)\text{\hspace{1em}(2.2)}$$

  如2.2式所示，使$G$与$D$的交叉熵最大的$D^{\ast }$即为最佳判别器。同样地，给定$D$，最小化2.2式的$G^{\ast }$就是最佳生成器，即：

$$G^{\ast }=\arg \underset{G}{\min }\underset{D}{\max }V(G,D)\text{\hspace{1em}(2.3)}$$

  下面推导$D^{\ast }$与$G^{\ast }$满足的具体条件。首先，将2.1式展开，得到

$$\begin{array}{rl}V(G,D)& ={\mathbb{E}}_{x\sim p_{data}(x)}[\log D(x)]+{\mathbb{E}}_{x\sim p_g(x)}[\log (1-D(x))]\\ & ={\int }_x{p}_{data}(x)\log D(x)dx+{\int }_x{p}_g(x)\log (1-D(x))dx\\ & ={\int }_x[p_{data}(x)\log D(x)dx+p_g(x)\log (1-D(x))]dx\end{array}\text{\hspace{1em}(2.4)}$$

  式2.4中，$D(x)$可取任何可微函数。令$f(D)$为被积函数，即：

$$f(D)=p_{data}(x)\log D(x)dx+p_g(x)\log (1-D(x))\text{\hspace{1em}(2.5)}$$

  在式2.5中，$D=D(x)$，$p_{data}(x)$是真实样本分布故相对$D$是给定的，显然$p_g(x)$也是固定的。则，对$f(D)$求导并令$f^{{}^{\prime }}(D)=0$，解得：

$$D^{\ast }=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}\text{\hspace{1em}(2.6)}$$

  式2.6即为给定$G$，性能最佳$D$应满足的数值特征。将2.6式代入2.1式，得：

$$\begin{array}{rl}\underset{D}{\max }V(G,D)& =V(G,D^{\ast })\\ & ={\mathbb{E}}_{x\sim p_{data}(x)}[\log D^{\ast }(x)]+{\mathbb{E}}_{x\sim p_g(x)}[\log (1-D^{\ast }(x))]\\ & ={\mathbb{E}}_{x\sim p_{data}(x)}[\log \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}]+{\mathbb{E}}_{x\sim p_g(x)}[\log \frac{p_g(x)}{p_{data}(x)+p_g(x)}]\\ & ={\int }_x{p}_{data}(x)\log \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}dx+{\int }_x{p}_g(x)\log \frac{p_g(x)}{p_{data}(x)+p_g(x)}dx\\ & =2\log \frac{1}{2}+{\int }_x{p}_{data}(x)\log \frac{p_{data}(x)}{\frac{p_{data}(x)+p_g(x)}{2}}dx+{\int }_x{p}_g(x)\log \frac{p_g(x)}{\frac{p_{data}(x)+p_g(x)}{2}}dx\\ & =2\log \frac{1}{2}+2\times [\frac{1}{2}KL[p_{data}(x)\Vert \frac{p_{data}(x)+p_g(x)}{2}]]+2\times [\frac{1}{2}KL[p_g(x)\Vert \frac{p_{data}(x)+p_g(x)}{2}]]\\ & =-2\log 2+2JSD(p_{data}(x)\Vert p_g(x))\end{array}\text{\hspace{1em}(2.7)}$$

  式2.7中，$KL$函数被称作$KL$（Kullback-Leibler Divergence，KL）散度^^[@r48]^，常用作度量数据集上的经验分布$p_{data}(x)$和生成数据分布$p_g(x)$之间的差异，其定义式如式2.8所示：

$$D_{KL}(p_{data}(x)\Vert p_g(x))={\mathbb{E}}_{x\sim p_{data}(x)}[\log (p_{data}(x))-\log (p_g(x))]\text{\hspace{1em}(2.8)}$$

  2.8式的左边仅涉及原始数据的分布，而与生成模型无关，这个事实简化了模型训练，即最小化$KL$散度等价于最小下式：

$$-{\mathbb{E}}_{x\sim p_{data}(x)}[\log (p_g(x))]\text{\hspace{1em}(2.9)}$$

  这能够给模型训练带来便利。值得一提的是，$KL$散度是非对称的，即：

$$D_{KL}(p_{data}(x)\Vert p_g(x))\ne D_{KL}(p_g(x)\Vert p_{data}(x))\text{\hspace{1em}(2.10)}$$

  为了解决$KL$散度非对称可能带来的不便，将其稍作变化就得到$JSD$（Jensen-Shannon Divergence）散度[50]，如式2.11所示。与$KL$散度类似，$JSD$散度也是用来度量两个概率分布的相似程度。

$$JS(P\Vert Q)=\frac{1}{2}KL(P\Vert \frac{P+Q}{2})+\frac{1}{2}KL(Q\Vert \frac{P+Q}{2})\text{\hspace{1em}(2.11)}$$

  一般地，$JS$散度是对称的，其取值为$[0,1]$。

  需要引起注意的是，在被度量的两个概率分布距离很远，完全没有交集的情况下，则$KL$散度值是无意义的，而$JS$散度值为常数。在模型训练过程中，这往往表现为某一点的梯度为0。

  据已得到的$D^{\ast }$，可以求出在给定$D$条件下使最小的$G^{\ast }$，如式2.12所示。

$$\begin{array}{rl}{G}^{\ast }& =\arg \underset{G}{\min }\underset{D}{\max }V(G,D)\\ & =\arg \underset{G}{\min }\underset{D}{\max }(-2\log 2+2JS(p_{data}(x)\Vert p_g(x))\end{array}\text{\hspace{1em}(2.12)}$$

  故，最小化$G$的需满足的数值特征为：

$$p_{data}(x)=p_g(x)\text{\hspace{1em}(2.13)}$$

  这与直观上的认知是一致的，即当生成分布$p_g(x)$同真实分布$p_{data}(x)$一致时，所对应的$\underset{D}{\max }V(G,D)$取最小值。在模型训练时，一般使用梯度下降的方式来使生成数据的分布不断拟合真实数据的分布，即：

$${\theta }_G:={\theta }_G-\eta \frac{\partial \underset{D}{\max }V(G,D)}{\partial {\theta }_G}\text{\hspace{1em}(2.14)}$$

  式2.14中，${\theta }_G$为每次迭代时生成器$G$所取梯度值。

  另外，由于在现实世界中，真实的样本空间一般都是无比庞大的，对于人所能采集到的有效样本而言，可谓是无穷大，故必须通过采集样本的概率分布来估算真实的样本分布。显然，采集样本属于离散值，因此需将2.7式的积分表达式改写为求和的形式，如式2.15所示。

$$V(G,D)=\frac{1}{m}\sum _{i=1}^m\log D(x^i)+\frac{1}{m}\sum _{i=1}^m\log (1-D(x^i)\text{\hspace{1em}(2.15)}$$

  在式2.15中，$x^{(i)}(i=1,2,...,m)$为真实分布$p_{data}(x)$的采样，$x^{(i)}(i=1,2,...,m)$为生成分布$p_g(x)$的采样。至此，最大化$V$的目标亦即最小化交叉熵损失函数$L$为：

$$L=-(\frac{1}{m}\sum _{i=1}^m\log D(x^i)+\frac{1}{m}\sum _{i=1}^m\log (1-D(x^i))\text{\hspace{1em}(2.16)}$$

  若将真实分布$p_{data}(x)$的采样$x^{(i)}(i=1,2,...,m)$视作正例，生成分布$p_g(x)$的采样$x^{(i)}(i=1,2,...,m)$视作负例，那$D$就是一个以梯度${\theta }_G$为判据的二分类器，可在模型训练时进行梯度下降获得性能最佳的$D^{\ast }$。

  本文通过以上分析，可以得到原始GAN的算法训练伪代码如下所示：

  原始GAN的训练可以形象地如图2.2所示[13]，在图2.2中，$z$指示随机噪声空间，$x$为真实数据空间，从$z$指向$x$的箭头指示生成器$G$的函数映射$x=G(z)$，黑色点划线、绿色实线与蓝色虚线依次指示真实分布$p_{data}(x)$、生成分布$p_g(x)$和判别器$D$。对于图2.2 a），模型刚开始训练，判别器$D$的能力较弱不足以区分真实数据与生成数据；对于图2.2
b），固定生成器$G$并按序优化生成器$D$，生成器$D$将逐渐收敛于$D^{\ast }$；对于图2.2 c），优化后的生成器$D$指导生成分布$p_g(x)$与真实分布$p_{data}(x)$的距离愈加小；对于图2.2 d），生成器所生成的样本与真实的样本一致，判别器失去判别两者差异性的能力，生成器与判别器达到纳什平衡（Nash Equilibrium），也意味着模型经训练已收敛。

原始GAN存在的问题

  在上一节中，本文详细分析了原始GAN的基本原理，从中可以看到，GAN具有从无标签的元数据学习数据概率分布的能力，在生成器$G$与判别器$D$二者的对抗训练中，这种能力被不断改善与强化，最终能够生成与元数据独立同分布的样本，GAN的对抗学习思想无疑是生成式深度学习算法的重要革新。原始GAN的理论效果极佳，但研究[35, 36, 37, 38, 39]发现GAN在实际应用中普遍存在以下问题：

  1）梯度消失

  训练原始GAN达到理想效果是一项极具挑战性的任务，主要表现之一为模型训练不稳定，其本质原因是在训练过程中，原始GAN的损失函数$JSD$散度丧失了衡量生成分布与真实分布距离的能力。本文2.1节阐述了理论上$JSD$可以指示两个概率分布之间的差异性，前提是二者彼此相距在可度量的范围内，当两个分布的距离"无穷远"，即$2JS(p_{data}(x)\Vert p_g(x)$等于$\log 2$时，此时判别器$D$的损失函数恒输出0（梯度消失），如式2.17所示。

$$\underset{D}{\max }V(G,D)=-2\log 2+2JS(p_{data}(x)\Vert p_g(x))=0\text{\hspace{1em}(2.17)}$$

  本文2.1节指出，采样数据是原始样本空间的甚小子集，样本的数据特征数量有限，故训练"充分"的判别器$D$有可能学习到所有特征，具备精准分割生成分布与真实分布的能力，而这说明对判别器$D$而言两个分布的差异无限大，二者的$JSD$散度为0。由此可见，判别器$D$的能力过强会导致产生过拟合现象，从而$JSD$度量失效。自然地，一个解决该问题的想法便是通过某些技术削弱判别器$D$，但原始GAN的初衷之一即是设计可以准确判别生成分布与真实分布的判别器$D$，如此便出现了矛盾。此外，由于生成数据是一个映射到高维空间的低维流形，而低维流形较少具备重叠的几何性质，此时也会出现$JSD$散度为0的情况。对于第二个问题有两种处置手段：其一是在生成样本分布和真实样本分布中嵌入噪声背景，增大二者产生交集的概率；其二是使用其他度量方式取代$JSD$散度，WGAN便是这种改进方式的代表。

  2）模式崩溃

  本文1.2.1节介绍过，原始GAN的生成器在无法和判别器同步训练更新的情况下，非常容易发生模式崩溃，其具体表现为生成器将过多的随机噪声用于压缩相同的真实数据，从而导致其没有足够的能力建模多样的生成数据。简而言之，即所有生成数据集中于某一个局部概率分布。该问题出现的具体原因，真实样本空间中交叉分布着数量充分多、数值偏高的概率分布，此处充分多的含义是足以引起生成器注视，生成器出于最小化由$KL$散度或$JSD$散度定义的损失函数的目的，会输出连续相同但多样性单一的样本。换言之，相同且高概率的分布在样本空间数量愈多，那么生成样本数量就可能愈单一，2.18式概要地表达了这个过程。

$$\begin{array}{rl}& When{p}_g(x)⟶0and{p}_{data}(x)⟶0,\\ & since{p}_g(x)\log \frac{p_g(x)}{p_{data}(x)}⟶01)\\ & When{p}_g(x)⟶+\infty and{p}_{data}(x)⟶0,\\ & since{p}_g(x)\log \frac{p_g(x)}{p_{data}(x)}⟶+\infty 2)\end{array}\text{\hspace{1em}(2.18)}$$

  结合上节本文对生成器与判别器输出不同数值时对应分布的描述，当出现2.18式）的情况时，意味着生成分布与真实分布差异大，$KL(p_g(x)\Vert p_{data}(x))$所得贡献趋近0，$KL$梯度对其惩罚甚小；而当出现2.18式）的情况时，意味着生成分布非常接近真实分布，$KL(p_g(x)\Vert p_{data}(x))$所得贡献趋近正无穷，$KL$散度对其惩罚甚巨。从此可以看出，$KL$散度纠正两种错误的手段截然相反，前者对应的是生成样本单一问题，而后者生成样本偏离真实分布。综述，生成器发生模式崩溃是最小化损失函数的必然结果。

  本文为了提高CDS-GAN训练的稳定性，采用梯度惩罚作为判别器损失函数的加权项，规避模式崩溃也是CDS-GAN模型设计的重中之重，本文对此的解决方法是基于Pix2Pix
GAN改进其生成器与判别器网络，并使用感知损失对目标函数进行优化，显著提高了生成含多样性表面缺陷的芯片图像的能力。

Pix2Pix GAN用于芯片表面缺陷数据增强

Pix2Pix GAN基本原理

  Pix2Pix GAN将目标域图像$x$与随机噪声$z$作为生成器$G$的输入，生成一张与原始样本独立同分布的图像$G(x,z)$；而判别器$D$将源域图像$x$与目标域图像$y$或源域图像$x$和生成图像$G(x,z)$作为输入进行判别。下面详细介绍图1.8中Pix2Pix的网络结构与目标函数。

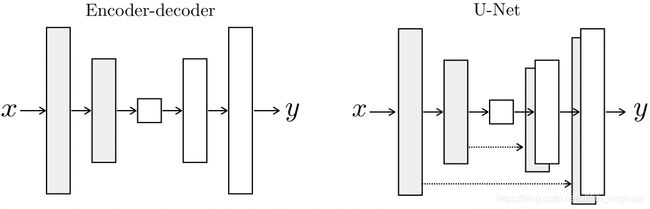
  Pix2Pix GAN的生成器$G$应用了编码器（Encoder）和解码器（Decoder）的结构，其选择U-net[51]作为生成器网络。U-net中将第$i$层的拼接至第$n-i$层，实现信息的流动与共享，因两者的特征图像尺寸一致，故可保存更多的有用信息。Pix2Pix的生成器$G$的结构如图2.3所示。Pix2Pix GAN的判别器$D$采用patchGAN，不同于一般的判别器将两张图像完整的作为输入，而输出一个经softmax规约后的$[0,1]$概率值来判定图像真伪。patchGAN将输入的两张图像各划分为$N\times N$块区域，两张图新的这些块经多层卷积取得特征值后依次一对一地判定，并将结果做softmax规约至$[0,1]$，如此输出一个$N\times N$、通道数为1的概率矩阵，再对该矩阵的元素值求数学期望得到最终patchGAN的输出。由于patchGAN采用了分块验证的思想，大大减少了参数量，并在保证判定效果的情况下速度提升显著。patchGAN的结构如图2.4所示。

  Pix2Pix GAN为保证生成图像与真实图像在低维特征的相似度，添加$L1$损失并同生成对抗损失组合为模型的损失函数，如式2.19所示。

$$L_{Pix2Pix}(G,D)=L_{cGAN}(G,D)+{\lambda }_1{L}_{L1}(G)\text{\hspace{1em}(2.19)}$$

  式2.19中，$L_{cGAN}(G,D)$为CGAN的生成对抗损失，其表达式如式2.20所示；$L1$损失的函数式，如式2.21所示。

$$L_{cGAN}(G,D)={\mathbb{E}}_{x,y}[\log D(x,y)]+{\mathbb{E}}_{x,y}[\log (1-D(x,G(x,z)))]\text{\hspace{1em}(2.20)}$$

$$L_{L1}(G)={\mathbb{E}}_{x,y,z}[{\Vert y-G(x,z)\Vert }_1]\text{\hspace{1em}(2.21)}$$

  Pix2Pix GAN的目标函数，如式2.22所示。

$$G_{Pix2Pix}^{\ast }=\arg \underset{G}{\min }\underset{D}{\max }{L}_{Pix2Pix}(G,D)\text{\hspace{1em}(4.22)}$$

Pix2Pix GAN生成芯片缺陷图像

  工业芯片所含表面缺陷的类型、面积、密度以及次品率与其制造工艺密切相关，例如：LED产品的封装流程主要有6个关键步骤，依次为：芯片固晶、金线键合、荧光粉胶涂覆、透镜安装、封装胶填充与模块集成[51]，其中金线键合是借助键合金线将芯片正负两极连通底座支架，使电信号可输入LED芯片，若金线崩裂或遗漏该步骤将造成"缺铜"表面缺陷，缺铜的直观表现是某细长条几何体丢失，属于长缺陷类型，单个出现；在进行荧光粉胶涂覆操作时，固定数量的荧光粉颗粒被散入环氧树脂或硅胶中形成荧光粉胶体，再借助涂覆设备将之点涂或喷涂至LED芯片表面并予以高温加热使之固化[52]，该步骤是产生"气泡"表面缺陷的主要来源，胶体中的某些物质发生化学反应产生氢气，在胶体中以气泡的形式呈现，气泡的大小相对固定，但数量分布取决于反应温度等条件。

  从上述讨论容易推论，应用Pix2Pix GAN对工业芯片表面缺陷图像进行数据增强时，有两个亟待解决的问题：

  1）准确定位缺陷位置与所占区域。原始GAN及其变种模型只能在学习原始图像后生成完整的图像，并且由于本文2.2节提及的模式崩溃问题，所生成图像所含缺陷的类型与位置分布或远未及预期。此外，本文的最终目的是将生成数据用于扩充原始数据集以提高分类器性能，因此需要获知生成图像中缺陷的类型与标签信息。

  2）完美复刻不同类型缺陷的几何形状、纹理、背景。生成缺陷应当具有高还原度，且能同周围芯片背景完美融合，以免突兀的背景差异致使后续操作中分类器学习到不必要的图像特征。

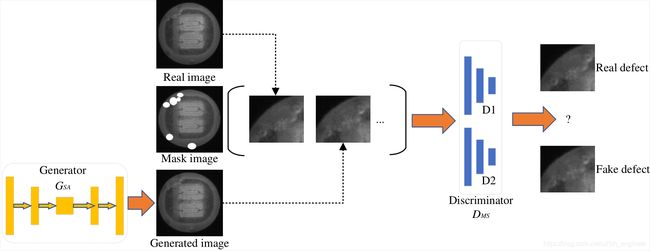
  本文创造性地使用mask图像解决了上述问题。基本流程如图2.5所示，图中生成器$G$与判别器$D$分别对应Pix2Pix GAN的相应模型。该方法的创新之处在于，以缺陷图像的缺陷位置与缺陷面积为基准，用mask在无缺陷图像对应之处进行标记。如此，便得到了一个图像对–含缺陷图像与带有mask的图像，将其作为生成器$G$的输入，那么模型将学习如何从mask图像转换为缺陷图像。本文采用mask约束的方法，解决了GAN生成缺陷位置随机，需重新打标签的问题，降低了人工成本，同时mask是可控的，这也意味着可指定缺陷生成在芯片图像范围的任何区域。

  采用mask有助于生成坐标可控的缺陷图像，但由于并未针对性地设计网络，仅依靠Pix2Pix GAN的图像翻译能力来达成目标。众所周知，Pix2Pix GAN是作为一个非专用图像翻译工具设计出来的[39, 40]，故其生成芯片缺陷图像并不理想，具体的实验结果将在本文第4章进行展示。遵循该理念，本文针对工业芯片表面缺陷的图像增强提出了Chip Defect Synthesis-GAN（CDS-GAN），创新性地采用ResNet取代U-Net作为生成器网络，且在其中添加了双层自注意力模块，同时使用了多尺度判别器，并应用WGAN-GP梯度惩罚对判别器损失函数进行约束，此外感知损失被用于辅助生成器生成更高质量的图像。一系列优化方法使该模型所生成的缺陷图像与其他GAN相比有显著提升。

本章小结

  本章首先详细分析了原始GAN的基本原理及其由结构设计造成的梯度消失与模式崩溃问题。GAN是一种基于"零和博弈"理论提出的无监督生成模型，可用于标签数据稀少而无标签数据繁浩的场景，学习原始数据的分布。GAN的模型训练，是一个生成器G与判别器D不断进行对抗学习的博弈过程。原始GAN采用模型优化方法是$JSD$（$KL$）散度定义的交叉熵损失；$JSD$（$KL$）散度是导致原始GAN梯度消失与模式崩溃的根本原因。

  其次，本文介绍了图像翻译的通用框架Pix2Pix GAN，该模型的生成器与判别器的设计均极有借鉴意义。同时本文提出了一种巧妙的将Pix2Pix GAN用于工业芯片表面缺陷生成的方法，该方法别具一格，很好地解决了生成缺陷类别不定、位置随机的问题。

用于工业芯片表面缺陷数据增强的CDS-GAN

  本文1.2.2节介绍了国内外学者使用GAN进行工业表面缺陷数据增强的工作，但正如本文总结的那样，这些研究在特定数据集可以取得较理想的实验室效果，但缺乏可迁移性，无法在其他数据集复现。在第二章，本文引入了一个多场景适用的图像翻译网络Pix2Pix GAN，将之用于工业芯片表面缺陷的图像增强。但直接采用Pix2Pix GAN生成缺陷样本的质量较低，效果不佳，故而本文提出了Chip Defect Synthesis-GAN（CDS-GAN）。

算法流程

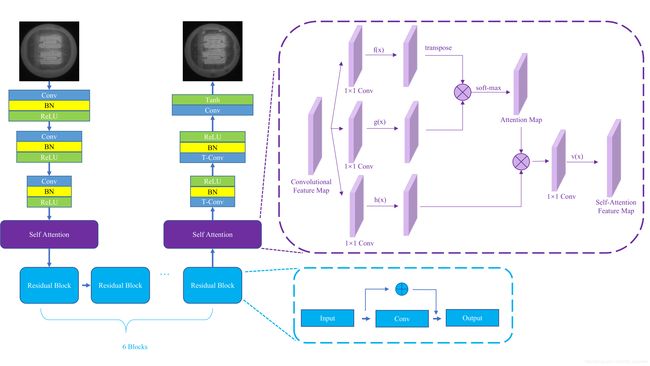
  本文提出的模型CDS-GAN基于Pix2Pix GAN进行改进，整体的网络结构如图3.1所示。与图1.8的Pix2Pix GAN模型结构进行对比，可以发现本文所设计的CDS-GAN改进方法是：生成器模型$G$采用ResNet结构替换U-Net结构，并在残差块（Residual Blocks）的首尾各添加一层自注意力网络；同时多尺度判别器MSD依次运用两种不同的感受野对生成图像进行判定；另外VGG网络将计算生成图像与真实图像在语义空间的信息差异，结果以感知损失的形式在反向传播中传递给生成器网络$G$；梯度惩罚函数对判别器的更新进行约束。其中，CDS-GAN在进行训练时模型的各个子网络按照既定步骤完成其任务。

  本文为使CDS-GAN更专注于合成芯片缺陷，用mask标记无缺陷图像的目标区域，目标区域由缺陷图像相应的缺陷坐标与面积决定，mask与缺陷图像对分别作为标签数据和目标图像输入CDS-GAN，从而帮助生成器$G$学习在mask处生成缺陷，进一步地，在该过程中自注意力模块辅助生成器$G$更多地关注芯片缺陷，同时抑制其他非重要特征。多尺度判别器MSD接收生成图像fake与真实图像real作为输入，用$size1$与$size2$两种尺度的判别器依次对fake图像与real图像进行分块裁决，该过程提高了多尺度判别器MSD区分输入图像对为mask-真实图像对还是mask-生成图像对的能力。与此同时，梯度惩罚模块以MSD为基准，计算该轮迭代中real图像与fake图像相应的WGAN-GP量值，约束下一轮MSD的更新梯度；随后经由VGG网络计算而得fake图像与real图像的感知损失与对抗损失一道反馈给生成器。各个子模块经由上述训练后，生成器G获得了在mask中合成极其还原缺陷的能力，而mask的坐标信息可用于后续的目标检测。从上述描述可以看出，本文所设计的CDS-GAN完全可胜任如下任务：基于少量标记缺陷图像生成高质量、特征丰富的缺陷样本，将其用做目标检测的数据增强。

  本章接下来将详细介绍CDS-GAN模型原理，即生成器与判别器的网络结构，以及本文针对CDS-GAN优化所设计的损失函数。CDS-GAN的实验结果与分析将在第4章详细阐述。

自注意力机制引导的生成器网络

  生成器$G$用于学习自输入到输出的条件映射：$G:x\to y$，其中$x$为输入的mask图像而$y$为含缺陷的目标图像。在本文所提CDS-GAN中，采用残差网络[53]作为基本框架，并结合自注意力机制[54]实现一种增强的解编码结构（Encoder-Decoder
Network）的生成器网络，其基本结构如图3.2所示。

残差模块

  深度神经网络自浅到深的每层网络可在不同抽象程度上提取数据特征，理论上，神经网络的网络层次越深，其对数据分布的拟合能力也将随网络参数的增加而增强，但实验发现，层次过多的神经网络往往存在训练困难的问题。仅仅依赖增加卷积神经网络的层数来提高网络性能不尽如人意，过深的神经网络性能会严重下降，甚至无法匹敌浅层网络。这种现象被称为"梯度消失"，其并非是因采用某种不恰当激活函数所致，如Sigmoid或Tanh，而是由于深层神经网络引起的结构性问题。梯度消失可以通过采用残差网络很好地解决，由残差模型组成的神经网络支持梯度在任意层，以反向传播的方式恒等流动到任一浅层网络，该方式与集合论中的恒等映射相似，因此被以此命名。恒等映射保证了神经网络参数的有效更新[53]，其实验效果如图3.3所示。

  本文为了使生成器$G$的生成能力充分强，足以拟合目标域的任意样本，同时避免上述的梯度消失问题，本文采用残差结构来保证有效的梯度跨层流动，在将网络参数量限制在一定阈值内的同时，增强了特征图的输出表达能力，传播效率也得到提升。本文所用残差模块的单元结构，如图3.4所示，显然与Pix2Pix GAN的U-net类似，这也是一种跳跃连接。

  本文所用残差学习的映射函数，如式3.1所示。

$$X_{l+1}=X_l+F(X_l)\text{\hspace{1em}(3.1)}$$

  在式3.1中，$X_l$是第$l$层残差块的输入，$X_{l+1}$为第$l+1$层的输出，而$F(X_l)$指示残差网络需学习的残差。

自注意力机制模块

  优秀的全局依赖关系建模能力对于生成器而言至关重要，但因其所用的卷积神经网络的卷积核大小的限制，生成器无法在有限的网络层次中捕获生成图像过程中的全局依赖信息，过深的神经网络会带来可观的时空复杂度以及上节所述的梯度消失问题。近几年，自注意力机制[55]在构建全局依赖属性上有着卓越的性能体现[56, 57, 58, 59]，其比同类方法所需的建模时间缩短，计算效率更高。

  自注意力机制最先是在计算机视觉领域被提出，其主要思想源于人眼的生物视觉注意力机制。譬如：人类在注视某幅图像，人眼不会也不可能一次性扫描图像的所有像素，亦或注意图像的每个细节，而是着重对某块感兴趣的区域进行审阅，从中发掘可能存在的重要信息，从而完成对该图的整体认知。在生成缺陷图像时，自注意力机制的采用将辅助CDS-GAN获得图像的全局特征，如：对于生成缺陷区域，自注意力机制将根据模块先前获知的全局特征图与当前局部区域之间的依赖关系，对缺陷区域进行构建。如此，将自注意力机制用于学习图像的全局特征，将之与图像的局部特征进行对比得出两者的依赖关系，能使生成图像与原始图像具有极高的语义相似性，尤其是引起自注意力模块关注的芯片缺陷。CDS-GAN在LED工业芯片数据集上训练时所生成的自注意力图像，如图3.5所示。自注意力机制不同于一般的多层卷积网络，因此计算量也得到大幅降低。

  本文使用的自注意力机制模块基本结构，如图3.6所示。

  自注意力机制的工作时序如下：起始，被前序卷积神经网络计算获得的图像特征映射作为自注意力模块的输入，两个$1\times 1$卷积分别对其作线性变换与通道压缩运算，各得到两个张量。接着两个张量被依次转换为特征矩阵，转置后执行矩阵乘法，而后再使用softmax运算将相乘的结果转换为注意力特征映射。与上述双卷积及其后续操作同时序的是，也采用$1\times 1$卷积对原始特征映射执行线性变换与通道压缩，并将结果转换为特征矩阵，再将其与先前所得注意力映射矩阵相乘，求和后得自注意力特征映射。自注意力特征映射同原始卷积特征映射加权求和的结果，作为自注意力模块的究极输出。在上述步骤中，自注意力特征映射可视作特征映射同自身转置的乘积，图像中相距较远的任两点的属性可通过此操作加强，故其能学习任意两像素点间的依赖关系，借以获知图像的全局特征。

  仅仅了解一个模型的工作流程不足以洞悉其内部机理，为了稳固CDS-GAN的理论基础，下面本文将从数学上推导自注意力机制的相关表达式。来自前一个隐藏层的图像特征$\mathbf{x}\in {\mathbb{R}}^{C\times N}$首先被转置为两个不同的特征空间$f$、$g$，用于下一步计算注意力特征映射，即：

$$\begin{array}{rl}\mathbf{f}(\mathbf{x})& ={\mathbf{W}}_{\mathbf{f}}\mathbf{x}\\ \mathbf{g}(\mathbf{x})& ={\mathbf{W}}_{\mathbf{g}}\mathbf{x}\\ {\beta }_{j,i}& =\frac{\exp (s_{ij})}{{\sum }_{i=1}^N\exp (s_{ij})}\end{array}\text{\hspace{1em}(3.2)}$$

  其中，

$$s_{ij}=\mathbf{f}({\mathbf{x}}_{\mathbf{i}}{)}^T\mathbf{g}({\mathbf{x}}_{\mathbf{j}})\text{\hspace{1em}(3.3)}$$

  式3.3中，${\beta }_{j,i}$指示模型在生成图像的区域$j$时对另一区域$i$的关注度，换句话说，区域$i$对合成区域$j$内容的贡献程度。假设图像的通道数为$C$，来自前一隐藏层的图像特征方位的数量为$N$，则注意力特征层的输出如式3.4所示。

$$\mathbf{o}=({\mathbf{o}}_1,{\mathbf{o}}_2,...,{\mathbf{o}}_{\mathbf{j}},...,{\mathbf{o}}_{\mathbf{N}})\in {\mathbb{R}}^{C\times N}\text{\hspace{1em}(3.4)}$$

  其中，

$$\begin{array}{rl}{\mathbf{o}}_{\mathbf{j}}& =\mathbf{v}\left(\sum _{i=1}^N{\beta }_{j,i}\mathbf{h}({\mathbf{x}}_{\mathbf{i}})\right)\\ \mathbf{h}({\mathbf{x}}_{\mathbf{i}})& ={\mathbf{W}}_{\mathbf{h}}{\mathbf{x}}_{\mathbf{i}}\\ \mathbf{v}({\mathbf{x}}_{\mathbf{i}})& ={\mathbf{W}}_{\mathbf{v}}{\mathbf{x}}_{\mathbf{i}}\end{array}\text{\hspace{1em}(3.5)}$$

  在式3.5中，${\mathbf{W}}_{\mathbf{g}}\in {\mathbb{R}}^{\bar{C}\times C}$，${\mathbf{W}}_{\mathbf{f}}\in {\mathbb{R}}^{\bar{C}\times C}$，${\mathbf{W}}_{\mathbf{h}}\in {\mathbb{R}}^{\bar{C}\times C}$，与${\mathbf{W}}_{\mathbf{v}}\in {\mathbb{R}}^{C\times \bar{C}}$均为以$1\times 1$卷积方式实现的学习权重指标，$\bar{C}$为通道数，实验发现增大其数值并未明显改善生成图像的质量，故本文取$\bar{C}=\frac{C}{8}$。

  注意力层的最终输出，如式3.6所示。

$${\mathbf{y}}_{\mathbf{i}}=\gamma {\mathbf{o}}_{\mathbf{i}}+{\mathbf{x}}_{\mathbf{i}}\text{\hspace{1em}(3.6)}$$

  式3.6中的$\gamma$为一个网络通过学习确定的参数，其初始值为0。自学习参数γ的引入允许网络首先依赖近邻的信息，而后逐渐学习分配更多权重到其他非邻近的特征上。

生成器网络结构

  本文在3.2节最初就给出了CDS-GAN生成器$G$的结构，其设计借鉴了深度残差网络，并且增加了自注意力机制模块以提升获取远距离依赖关系的本领，共包含3个部分：前部为3层深度卷积神经网络，而后接合1个自注意力模块，中部乃7层深度残差神经网络，其后也连接1个自注意力模块，后部是2层深度转置卷积神经网络与1层深度卷积神经网络，总计15层。每层网络的通道数已在图3.2中给出标注，在此不赘述。值得一提的是，生成器$G$在计算特征图的卷积前会做边缘补零（Zero-Padding）的预处理，避免图像边缘的信息在传播过程中发生丢失，同时保证张量的输入输出维度一致。批归一化（Batch Normalization）[58]是卷积计算后的必要操作，其有利于网络参数保持标准的高斯分布，并缩减特征图中通道均值与方差的不一致对生成图像的负面效果，此外可加速模型收敛，对模型稳定性与泛化性的加强也有一定增益。卷积网络与转置卷积网络均采用ReLU（Rectified Linear Unit）[59]作为激活函数，$ReLU$函数的定义如式3.7所示。其中，不同分辨率的特征图依次经由转置卷积网络完成上采样，而后通过$3\times 3$卷积进行转发，输出不同分辨率的图像。最终结果再经$Tanh$函数压缩至$[0,255]$输出，$Tanh$函数的定义如式3.8所示。

$$ReLU(x)=f(x)=\max (0,x)\text{\hspace{1em}(3.7)}$$

$$Tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{1-e^{-2x}}{1+e^{2x}}\text{\hspace{1em}(3.8)}$$

多尺度感受野的判别器网络

  判别器$D$以真实缺陷图像中的缺陷作为正样本，另将生成图像中的芯片缺陷作为负样本，在模型训练过程中学习判别mask图像对应区域的缺陷真伪。如此，判别器$D$将促进生成器$G$学习在正常图像mask对应处生成缺陷。为使生成图像具有更好的全局连续性以及更加精细的结构，需从整体与局部的不同尺度对图像块进行建模，故此本文提出了一种多尺度判别器（Multi-Scale Discriminator，MSD），其对不同分辨率的图像依序采用不同的感受野判别各图像块。MSD的基本结构，如图3.7所示。

多尺度技术

  多尺度技术（Multi-Scale Technique）亦被称作多分辨率技术（Multi-Resolution Analysis），是指采用不同尺度的特征映射对不同尺度的数据做既定处理。同3.2.2节阐述的自注意力机制一样，多尺度技术也是仿生学在计算机图像处理领域的具体应用，其类似于人眼的感知机制，即：人眼距离观测物体较近时可以感知它的局部细节，而当远离观测物体时则能够识别其几何形状与外观轮廓等全局信息，显然，两种在不同观测尺度下获知的信息结合方才能完整、翔实地描述该物体。相似地，计算机无法在单一尺度下获取数据完整的特征，而多尺度条件下计算机获取特征的类别、数量及质量都显著提升。本文的数据为工业芯片缺陷图像，图像需要定义不同尺度的测度方能正确进行多尺度表达。本文按照不同多尺度方法的实现结构，将其划分为以下四类：

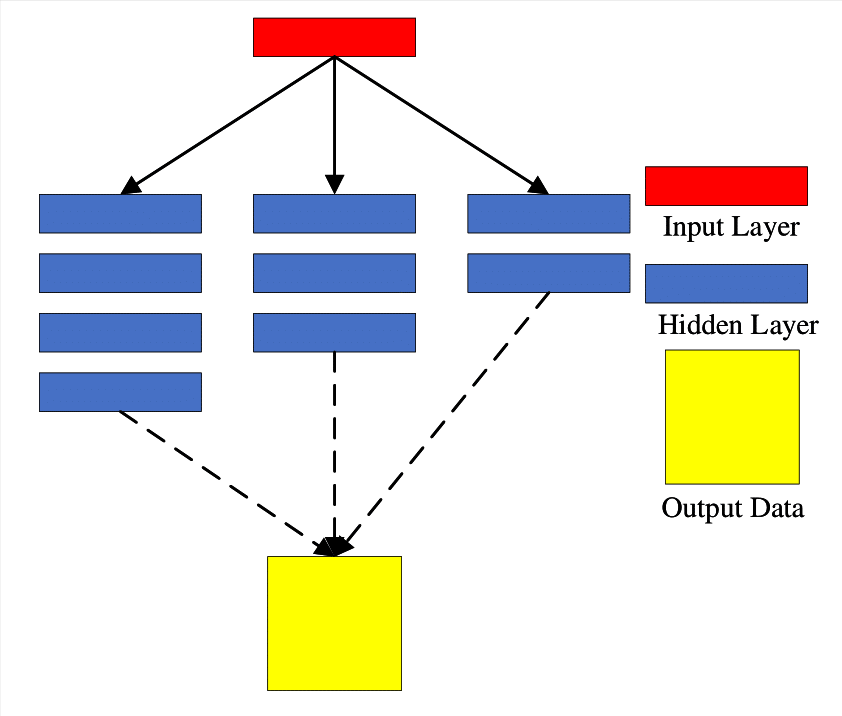
  1）多通道结构[61]，这种多尺度实现方法将图像输入多个网络分支，经由不同尺度的卷积计算，而后把级联的不同卷积计算结果传递至输出层，作为最终结果。Inception网络的Inception模块是多尺度方法以多通道结构实现的典型代表，其拓补结构如图3.8 a）所示。

  2）跳跃结构[63, 63]，此种多尺度实现方法将不同层级的网络的结果整合后输入至一共享输出层，该结构实现多尺度方法的典型代表是FCN（Fully Connected Network），其拓补结构如图3.8 b）所示。

  3）多输入单模型结构[64]，应用这种结构的目的一般是为了实现多尺度预测，而将多尺度的数据至同一个网络中，该结构简单实用，训练及测试过程均适用，其拓补结构如图3.8 c）所示。



  4）整体嵌套结构[65]，采用这种实现方法的网络组成只含一个单独支路，多个预测结果经由这条总支路的某一侧输出，这些预测值加权求和的结果作为最终输出，网络的拓补结构如图3.8 d）所示。

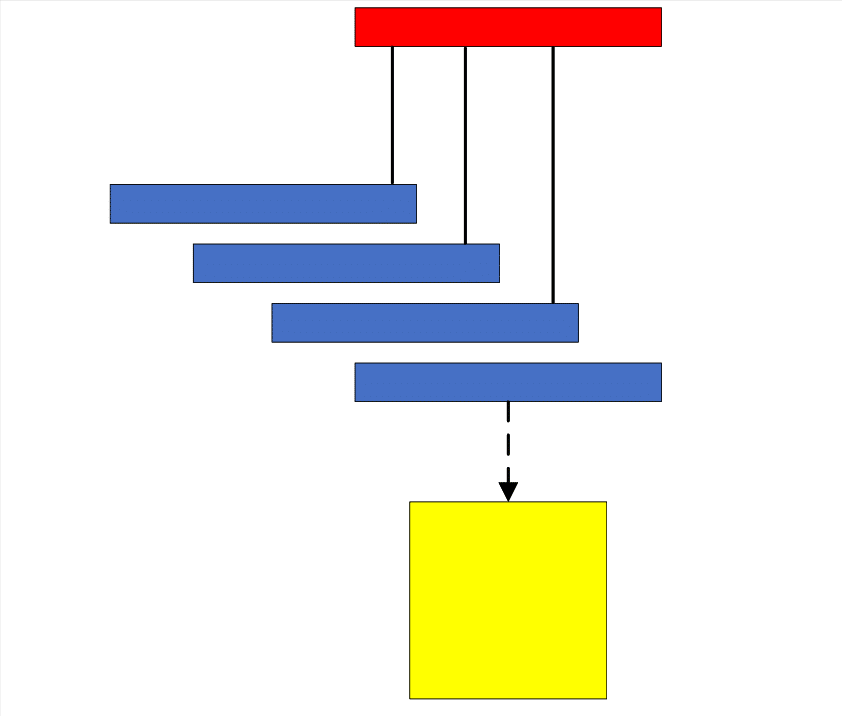
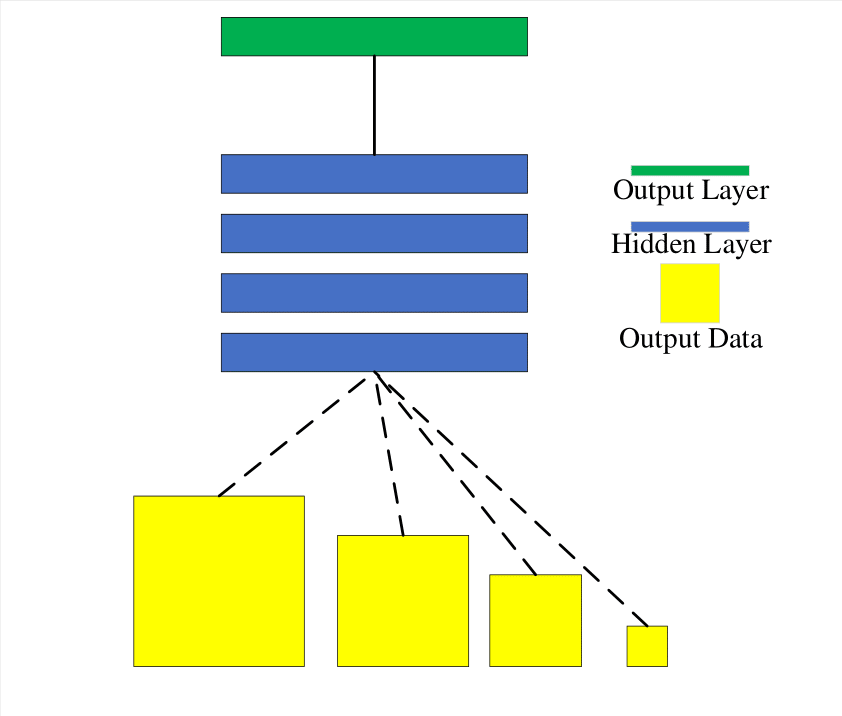
多尺度判别器

  因原始patchGAN感受野为$70\times 70$，远大于芯片缺陷的面积，导致判别器对缺陷区域不敏感，Jaipuria等^^[@r65]^通过实验表明感受野与生成图像的语义内容差异直接相关，故减少判别器的感受野可以减少翻译过程中的语义内容差异。针对于此，本文设计了一个多尺度判别器，即将工业芯片缺陷图像与生成图像或真实无缺陷图像各对半缩减，而后将原始分辨率及分辨率减半的缺陷芯片图像和真实无缺陷图像或生成图像分别输入两个结构一致的patchGAN判别器$D_1$，$D_2$。具体地，$256\times 256$图像对由感受野较大的$D_1$判别，引导生成器$G$合成全局连续光滑的芯片区域；感受野较小的$D_2$判别$128\times 128$图像对，引导生成器$G$合成更加细密精致的缺陷，MSD工作流程如图3.9所示。显然，多尺度感受野可以在保证原有的语义信息不丢失的情况下，提高识别缺陷区域的能力。

融合感知损失与梯度惩罚的损失函数

  GAN的损失函数用于优化网络以及约束模型的参数更新，选择恰当的损失函数可以极大改善GAN的效果。由于GANs中的对抗损失更多关注的是图像的全局分布，并不适用于芯片图像在背景、缺陷纹理等方面的细节生成。Pix2Pix GAN使用$L1$函数[38]来保证输入与输出在像素层的相似度，但这并不足以其在语义信息上的缺失。因此，本文在CDS-GAN网络框架中引入感知损失对图像高级语义特征以及图像的局部结构进行约束优化。

  此外，本文使用WGAN-GP梯度惩罚作为判别器损失的加权项，1.2.1节曾介绍WGAN-GP较之WGAN能够使模型更快地收敛，生成样本的类别更丰富，WGAN-GP更从根本上解决了GAN训练不稳定与模式崩溃的问题。

  本文所设计模型CDS-GAN总的损失函数，如式3.9所示。

$$L_{CDS-GAN}(G_{SA},D_{MS})={\lambda }_1{L}_{adv}(G_{SA},D_{MS})+{\lambda }_2{L}_{pixel}(G_{SA})+{\lambda }_3{L}_{perc}(G_{SA})+{\lambda }_{4}GP\text{\hspace{1em}(3.9)}$$

  目标函数，如式3.10所示。

$$G_{CDS-GAN}(G_{SA},D_{MS})=\arg \underset{G}{\min }\underset{D}{\max }{L}_{CDS-GAN}(G_{SA},D_{MS})\text{\hspace{1em}(3.10)}$$

  式3.9中，$L_{adv}$指示生成对抗损失，$L_{pixel}$指示像素损失，$L_{perc}$指示感知损失，$GP$指示WGAN-GP梯度惩罚，$G_{SA}$与$D_{MS}$分别为本文3.2节和3.3节所设计的自注意力机制引导的生成器以及多尺度感受野的判别器，下面逐一详细介绍损失函数。

生成对抗损失

  本文所提出的模型CDS-GAN的生成对抗损失如式3.11所示。

$$L_{adv}(G_{SA},D_{MS})={\mathbb{E}}_{x,y}[\log D_{MS}(x,y)]+{\mathbb{E}}_{x,y}[\log (1-D_{MS}(x,G_{SA}(x,z)))]\text{\hspace{1em}(3.11)}$$

  式3.11中，$x$指示mask图像，$y$指示所生成的含表面缺陷的目标图像，$z$代表随机噪声。

像素损失

  CDS-GAN采用$L1$损失函数计算生成图像与目标图像在像素空间的欧氏距离，如式3.12所示。

$$L_{pixel}(G)={\mathbb{E}}_{x,y,z}[{\Vert y-G(x,z)\Vert }_1]\text{\hspace{1em}(3.12)}$$

  式3.12中各变量的含义与式3.11相同。

感知损失

  不同于像素级损失函数依赖于像素间的欧式距离,感知损失依赖于高级语义特征的差异，一般这些高级特征通过预训练的网络进行提取。VGG^^[@r66]^被广泛用于提取图像的语义特征，VGG是一个卷积神经网络架构的总称，被学者普遍研究的有6种，以网络深度区别命名，自浅至深分别为VGG1l，VGG11-LRN，VGG13，VGG16，VGG16-Convl，VGG19。其中，VGG11-LRN增加了局部响应规范化(local respond normalization, LRN)约束，而VGG16-Convl的设计增添卷积核为$1\times 1$的卷积层。一般的VGG卷积神经网络采用由大小为$3\times 3$的卷积核(Conv3)构成的卷积层,池化层和全连接层组成。因VGG采用较小的卷积核，故同其他卷积核较大的浅层网络相比，增加其网络层数所带来计算量幅度甚小，且得益于较深的网络结构，VGG具备更强的语义提取能力。

  本文通过实验对比，发现VGG11最适合于CDS-GAN，故本文使用在ImageNet上预训练的VGG11提取特征图，VGG11的网络结构如表3.1所示，此外，在每一层卷积层后都添加一个$ReLU$激活函数。

  用基于ImageNet预训练过的VGG11网络作为损失网络$\varphi$提取图像语义特征(如图3.10所示)，并计算生成样本与目标样本在特征图上的距离，通过缩小该距离，使两者在深度卷积神经网络上表现的语义分布更为接近。其目标函数$L_{PERC}$函数式，如式3.13所示。

$$L_{PERC}(G)={\mathbb{E}}_{x,z}[\frac{1}{C_j{H}_j{W}_j}{\Vert {\varphi }_j(x)-{\varphi }_j(G(x,z))\Vert }_2^2]\text{\hspace{1em}(3.12)}$$

  式3.13中，${\varphi }_j$表示VGG-11网络第$j$层（一般选择第3个block的第3层）特征，而后将宽（$W_j$）、高（$H_j$）和通道（$C_j$）3个维度的数学期望作为生成缺陷芯片图像$G(x,z)$与真实缺陷芯片图像$x$的感知损失。

梯度惩罚

  本文选取WGAN-GP[36]梯度惩罚用以约束判别器的更新，WGAN-GP是对WGAN的改进，而WGAN是基于Wasserstein距离所设计实现的模型。Wasserstein距离又称作Earth-Mover(EM)距离，其定义如式3.14所示。

$$W({\mathbb{P}}_r,{\mathbb{P}}_g)=\underset{\gamma \in \Pi ({\mathbb{P}}_r,{\mathbb{P}}_g)}{\inf }{\mathbb{E}}_{(x,y)\sim \gamma }[\Vert x-y\Vert ]\text{\hspace{1em}(3.14)}$$

  WGAN模型创造性地构造了一个判别器$D$，$D$满足条件：包含给定参数$w$且最后一层不是非线性激活层，另外在保持$w$波动不超过某个阈值的条件下，令

$$\begin{gathered} L={\mathbb{E}}_{x\sim p_{data}}[D(x)]-{\mathbb{E}}_{x\sim p_g}[D(x)] \\ ,wherex=G(z)\text{\hspace{1em}(3.15)} \end{gathered}$$

  式3.15尽可能趋向最大值，在该情况下，若忽略掉常数K，则L可近似为真实分布与生成分布之间的Wasserstein距离。

  WGAN虽性能优异，但从工程上来看，其较之原始GAN只改进了以下4点:

  1）判别器最后一层剔除sigmoid激活函数；

  2）生成器与判别器的损失函数值loss不取log对数；

  3）每次判别器的参数更新之后将其绝对值截断至不超过某个阈值；

  4）弃用基于动量的优化算法(包括Momentum和Adam)，而荐举RMSProp与SGD。

  WGAN-GP在WGAN的基础上做出改进，使用一个1-Lipschitz函数对约束函数L进行梯度惩罚，所谓1-Lipschitz函数是指满足条件当且仅当其梯度小于或等于1的范数时的可微函数，梯度惩罚的函数式如式3.16所示。

$$L={\mathbb{E}}_{\overline{x}\sim p_{data}}[D(\overline{x})]-{\mathbb{E}}_{\overline{x}\sim p_g}[D(\overline{x})]+\lambda {\mathbb{E}}_{\hat{x}\sim p_{\omega }}[(\Vert {\nabla }_{\hat{x}}D(\hat{x}){\Vert }_2-1){)}^2]\text{\hspace{1em}(3.16)}$$

  同WGAN的目标函数类似，WGAN-GP生成器及判别器的loss不取log。本文中，$\overline{x}\sim p_{data}$指示缺陷芯片及其分布，$\overline{x}\sim p_g$指示生成芯片及其分布，$\hat{x}\sim p_{\omega }$指示随机采样及其分布，$L$满足式3.16的定义。

  梯度惩罚函数的本质，即使用Lipschitz函数将判别器的梯度约束在$K$的范围内，具体地，先计算判别器的梯度，再构建其与常数$K$的二范数。对于梯度惩罚项来说，本文在每一轮的真实缺陷芯片图像与生成缺陷芯片图像中做一个插值$\hat{x}$：

$$\hat{x}=x\times \theta +x\times (1-\theta )\text{\hspace{1em}(3.17)}$$

  这里$\theta$指示服从均匀分布$\mathbb{U}[0,1]$的随机数。较之WGAN，WGAN-GP有以下3个优势：

  1）其在WGAN基础上采用梯度惩罚项对Wasserstein距离进行约束，规避WGAN模型有可能产生的训练波动大以及生成数据病态的症结；

  2）其收敛速度更快，生成样本质量亦更高；

  3）其适应性更强，在不同图像翻译框架中都可得到稳定的训练结果。

  最终，综合上述所有损失函数即可得到用于更新优化CDS-GAN参数的总损失函数，如式3.9所示。其中，${\lambda }_1$、${\lambda }_2$、${\lambda }_3$与${\lambda }_4$都是用于控制相应损失分量对总损失值的贡献，本文经由实验发现，依次取1、100、0.1和0.0001所取得的效果最佳。4种不同损失函数的加权和控制CDS-GAN模型参数的更新与优化方向贯穿整个训练始终。

本章小结

  针对原始GAN生成图像多样性低、质量较差且训练不稳定、极易发生模式崩溃的问题，而现有的变种GANs合成缺陷芯片图像的效果不理想，本文设计了一种专门用于生成工业缺陷芯片的GAN模型。原始GAN与当下流行的GANs大都是基于自然图像的机器视觉任务而提出来的，故无法直接用于工业表面缺陷的图像增强。值得一提的是，本文所提出的模型不仅在工业芯片缺陷生成的任务中表现良好，且同样适用于其他工业表面缺陷数据集，更在公开数据集上较之其他GANs表现卓越。

  为了提升含表面缺陷的工业芯片的合成效果，本章提出了自注意力机制引导生成器结合多尺度感受野判别器在生成对抗损失、像素损失、感知损失与梯度惩罚多条件约束下的生成对抗网络：Chip Defect Synthesis-GAN（CDS-GAN）。CDS-GAN的生成器$G_{SA}$以深度残差网络为框架，并通过添加自注意力模块，增强了生成图像时获知像素间远距离依赖的能力，提升了合成图像的质量。判别器$D_{MS}$采用了多尺度架构，加强对所生成图像的缺陷区域敏感性，在增强芯片缺陷判别能力的同时促使生成器GSA合成图像与原始图像语义内容更相似。感知损失强化了生成器$G_{SA}$对生成图像高级语义特征的约束，使生成图像与原始图像在视觉感知上更为接近；同时梯度惩罚项的加入避免了判别器$D_{MS}$领先生成器$G_{SA}$过快地更新，从而带来训练不稳定、模式崩溃等问题。

  综上，CDS-GAN生成含表面缺陷的工业芯片图像不仅质量高，且多样性丰富，更避免原始GAN的结构性问题。为了证明CDS-GAN的有效性与优越性，下一章将基于多个数据集对其进行训练测试，展示其生成图像并做数值评估，同时适用生成图像扩增后的数据集与原始数据集去训练SSD分类器，说明最终的数据增强效果。为了增强实验的说服力，本文将CDS-GAN与基准模型Pix2Pix GAN以及其他GANs的实验结果进行对比分析。

芯片表面缺陷数据增强实验与评估

  为了表明本文所提模型可用于工业芯片表面缺陷的数据增强任务，本章将在多个LED芯片与GPP芯片两个数据集上测试CDS-GAN，并对实验生成的图像进行展示。同时为了定量评估CDS-GAN的性能，本文测量对比生成图像与目标图像之间的FID、SSIM与PSNR值。此外，工业芯片表面缺陷的数据增强是本文工作的最终落脚点，故本文用原始缺陷芯片数据集A以及加入Pix2Pix GAN生成图像后的扩增数据集B、加入CDS-GAN生成图像后的扩增数据集C对SSD模型[69]进行训练。SSD（Single Shot MultiBoxDetector）[69]是一个单阶段目标检测算法，其使用VGG-16作为骨干网络进行特征提取，采用第6与第7深度卷积网络取代了原有的FC6及FC7，并追加了4个深度卷积网络。SSD借鉴了分层提取特征的思想，较好地平衡了检测精度与检测速度，是目前主流的目标检测模型之一。本文使用LED芯片与GPP芯片的原始数据集A与扩增数据集B、C来训练SSD检测器，通过比较三者的分类准确率即可得知数据增强的具体效果，以及本文模型CDS-GAN与Pix2Pix GAN孰优孰劣。

  更进一步地，为了证明本文模型的泛化性与鲁棒性，即说明CDS-GAN也可以用于其他工业表面缺陷数据集的增强任务，还支持通用的自然图像翻译，因此本文选取了磁瓦缺陷图像[1*]、桥梁裂缝图像[2*]、cityscapes[3*]、facades[4*]与maps[5*]等数据集分别训练CDS-GAN与Pix2Pix GAN，并采用上述4个指标对比分析。

  不得不提的是，本文所使用的实验环境为Intel ® Xeon ® E5-2618L v3
CPU，64位的Ubuntu 18.04，使用NVIDIA 1080 Ti型号的GPU加速网络模型训练，采用Python语言进行编程，并借助开源的PyTorch深度学习框架构建网络。CDS-GAN、Pix2Pix GAN与CycleGAN模型训练均采用Adam[72]算法进行优化，所用的超参数如表4.1所示，其他实验的超参数不在表中或有所改动，将在介绍具体实验时予以说明。

实验数据集

数据集介绍

  本文所用工业芯片数据集已在1.3.1节中介绍并展示过，不再赘述。除了两种工业芯片缺陷数据集外，为了表面CDS-GAN模型具有可迁移性，本文拣选了其他两种磁瓦缺陷图像与桥梁裂缝图像的工业缺陷数据集以及cityscapes、facades与maps自然图像数据集，用于对比训练CDS-GAN与Pix2Pix GAN的效果，各个数据集的示例，如图4.1与图4.2所示。

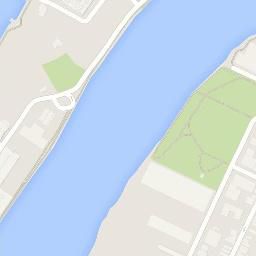
数据预处理

  由于缺陷芯片的原始数据量较小，无法充分体现模型性能，本文使用复制粘贴与传统的数据增强方式对数据进行扩充，将扩充所得的数据与原始数据进行分组，得到了实验最终的训练和测试数据集。其中，其中LED原始缺陷图像有198张，GPP原始缺陷图像有240张。

  本文参照Pix2Pix GAN论文使用的maps数据集，缺陷芯片数据集的结构格式如图4.3所示，每个文件夹下的图像数量相等。

  本文采用随机HSV色彩空间变换、高斯随机噪声、边缘模糊以及旋转、缩放、平移、裁剪4种仿射变换随机选取3种，对GPP原始数据集进行数据增强，将480张增强图像与原始GPP数据集组合得到"560"数据集；将原始GPP数据集复制粘贴12次，得到"1040"数据集。同560数据集类似，对LED原始数据集进行数据增强，将198张增强图像与原始LED数据集组合再经3次复制得到"792"数据集；将原始LED数据集复制粘贴5次，再删减180张特征不明显的图像，得到"1098"数据集。

评价指标

  为了便于定量评估CDS-GAN生成图像的质量与多样性，本文选择了3种在计算机视觉领域广泛用于度量图像相似程度的指标，即FID、SSIM与PSNR，其中前者是普遍用于评价GAN生成样本的数值依据，后两者为经典的图像结构相似度评价指标。

  1）FID

  FID[69]是计算真实图像和生成图片的特征向量之间距离的一种度量。首先，通过将真实数据和生成数据输入Inception V3网络，在分类层的前一个池化层将结果输出，分别得到两份数据的特征向量；接着计算特征向量的均值和协方差，将特征向量归纳为一个多变量高斯分布；最后，使用Wasserstein-2距离来计算两个分布之间的距离。图像生成质量越好，其与真实图片之间的Wasserstein-2距离越小，FID越低，反之，图片生成质量越差，其与真实图片之间的Wasserstein-2距离越大，FID越高。当两份数据完全一样时，FID值为0。FID的计算式如式4.1所示。

$$FID(X,G)={\Vert {\mu }_x-{\mu }_g\Vert }_2^2+Tr(\sum _x+\sum _g+2(\sum _x\sum _g{)}^2)\text{\hspace{1em}(4.1)}$$

  2）SSIM

  SSIM是一种模仿人类视觉感知的图像相似度评价指标，常用来测度两幅图像级别的相似度，该值越大表示两幅图像之间越相似，算法性能越好。SSIM的计算式如式4.2所示。

$$SSIM(x,y)=[l(x,y){]}^{\alpha }[c(x,y){]}^{\beta }[s(x,y){]}^{\gamma }\text{\hspace{1em}(4.2)}$$

  式4.2中，$x$与$y$分别为真实图像与生成图像，$\alpha$、$\beta$、$\gamma$为大于0的常数，用于计算图像三种数值对SSIM的贡献，即亮度比较$l(x,y)$、对比度比较$c(x,y)$、结构比较$s(x,y)$，三者的计算公式如式4.3所示。

$$\begin{array}{rl}l(x,y)& =\frac{2{\mu }_x{\mu }_y+c_1}{{\mu }_x^2+{\mu }_y^2+c_1}\\ c(x,y)& =\frac{2{\sigma }_{xy}+c_2}{{\sigma }_x^2+{\sigma }_y^2+c_2}\\ s(x,y)& =\frac{{\sigma }_{xy}+c_3}{{\sigma }_x{\sigma }_y+c_3}\end{array}\text{\hspace{1em}(4.3)}$$

  式4.3中，${\mu }_x$和${\mu }_y$指示$x$与$y$的期望，${\sigma }_x$与${\sigma }_y$指示$x$和$y$的标准差，${\sigma }_{xy}$指示$x$与$y$的协方差，而$c_1$、$c_2$与$c_3$为常数，主要作用是避免除零错误。

  3）PSNR

  鉴于本文所用数据集有可供参考的正常样本图像，因此，本文选择峰值信噪比（PSNR）来作为算法评价指标，峰值信噪比常用于生成图像的质量，PSNR值越高说明生成图像的质量与目标图像越接近。PSNR的计算式如式4.4所示。

$$PSNR=10\cdot {\log }_{10}\frac{MA{X}_I^2}{MSE}\text{\hspace{1em}(4.4)}$$

  式4.4中，$MA{X}_I^2$表示图像可能的最大像素值，若每个像素均由$N$位二进制表示，则$MA{X}_I^2=2^B-1$；式4.4中的另一个变量$MSE$为参与对比的两张图像的像素均方误差，如用$I$指示原始图像，$K$指示生成图像，两者尺寸均为$m\times n$，，那么MSE的表达式如式4.5所示。

$$MSE=\frac{1}{mn}\sum _{i=0}^{m-1}\sum _{j=0}^{n-1}[I(i,j)-K(i,j){]}^2\text{\hspace{1em}(4.5)}$$

  式4.5中，$i$与$j$指示像素的坐标。

  4）mAP

  mAP全称Mean Average Precision，意为数据集中各类标注物体的分类精度的数学期望，常用于评价分类器的性能。mAP的计算取决于各类类别的AP，而AP的数值为PR（Precision-Recall）曲线与坐标轴所围成的面积。Recall是另一个常用的分类器评价指标，Precision与Recall可通过混淆矩阵（Confusion Matrix）进行定义，如表4.2所示。

  在表4.2中，$TP$与$FP$各指示正样本预测为真的数量、负样本预测为假的数量，而$TN$和$TP$分别指示负样本预测为假的数量、正样本预测为为假的数量。显然，混淆矩阵中的$TP$与$TN$分别表示被正确预测的芯片缺陷与芯片背景。具体地，准确率（Precision）定义为被分类器正确预测的正样本占被分类器预测为正样本的比例，召回率（Recall）定义是分类器正确预测的正样本占全体正样本的比例，二者计算公式如式4.6与式4.7所示。

$$Precision=\frac{TP}{TP+FP}\text{\hspace{1em}(4.6)}$$

$$Recall=\frac{TP}{TP+FN}\text{\hspace{1em}(4.7)}$$

  从Precision与Recall的定义容易推知，当数据集中的正负样本极端不均衡时，两者的数值将失去参考意义。为此，AP作为Precision与Recall的改进和补充被提出。若令Recall为横坐标，Precision为纵坐标，描绘出二者的一一对应关系，则得到不同召回率下的分类精确率曲线，即PR曲线，故可得一般的AP定义，如式4.8所示。

$$AP={\int }_0^{1}P(R)dR\text{\hspace{1em}(4.8)}$$

  式4.8中的$P(R)$指示Precision，$R$指示Recall，通常某目标检测算法在一个数据集上的mAP愈大，则表明其性能愈优异。

  除此以外，误检率（False Detection Rate）与漏检率（False Dimissal Rate）也常被作为缺陷检测的重要指标，二者的计算公式分别如式4.9和4.10所示。

$$FalseDetectionRate=\frac{FP}{FP+TN}\text{\hspace{1em}(4.9)}$$

$$FalseDimissalRate=\frac{FN}{FN+TP}\text{\hspace{1em}(4.10)}$$

提取图像语义的最佳网络

  本文使用感知损失来监督生成器在语义特征级别的选择性表达，提高生成缺陷芯片样本与真实缺陷样本的语义相似性，从而使得生成缺陷芯片图像在人眼主观感受上更趋近于真实缺陷芯片图像。提取图像语义特征一般基于预训练的卷积神经网络实现，VGG系列是较为相符的抉择。被普遍讨论的VGG有6种，网络最深的是VGG19，网络层数最小的为VGG11，本文分别采用这两个网络以及层数折中的VGG16作为提取图像语义的骨干网络，实验结果如图4.4所示。

  从图4.4可以看到，当FID值趋于稳定后采用VGG11提取图像语义差异作为感知损失所生成图像的FID值，较之使用VGG16与VGG19更低，即生成缺陷芯片图像与原始缺陷芯片图像更相似且多样性更好。因此，在本章余下的实验中，本文选择VGG11作为提取图像语义特征的主干网络。

在具体数据集上的实验结果

  本章的剩余内容主要是在各个数据集上验证CDS-GAN的效果，同时会与Pix2Pix GAN以及其他变种GANs的性能进行横向比对。

LED芯片图像数据集

  LED缺陷芯片图像一共包含3个数据集，依次是66数据集、792数据集与1098数据集。本文用66数据集和792数据集分别训练CDS-GAN与Pix2Pix GAN，此外1098数据集被用于训练CDS-GAN及Pix2Pix GAN、CycleGAN、DCGAN、WGAN-GP，用作训练的LED缺陷芯片-mask图像对如图4.5所示，下面将从定性与定量两个方面对实验结果进行分析。需要说明的是，在使用66数据集进行训练时，CDS-GAN、Pix2Pix GAN的n_epochs与n_epochs_decay分别取150，其他与表4.2保持一致；另外，DCGAN、WGAN和WGAN-GP的模型训练超参数如表4.3所示，下文如无特殊声明则三者的超参数维持表中的设置。

  1）定性评估

  如图4.6、图4.7与图4.8所示，CDS-GAN和Pix2Pix GAN分别基于66数据集、792数据集、1098数据集训练后所生成的LED缺陷芯片图像与原始缺陷芯片图像的对比。从视觉效果上看，Pix2Pix GAN所生成的图像背景较为模糊，纹理不够自然，生成的气泡缺陷几何形状不连续、规整，而我们的模型所生成的芯片图像背景与原图更接近，缺陷的纹理与原图极大地相符，生成的气泡缺陷形状完整、连续清晰，这是因CDS-GAN增添了自注意力机制。此外，通过对比CDS-GAN基于这三个数据集上生成的LED缺陷芯片，易发现仅凭人眼无法轻松地区分哪个数据集的生成样本最佳，即难以体现数据集规模增减所带来的性能变化。

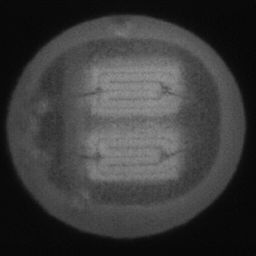
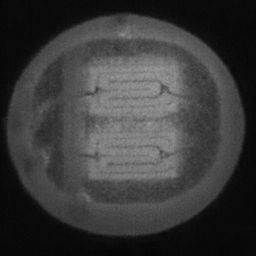
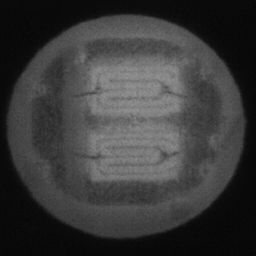
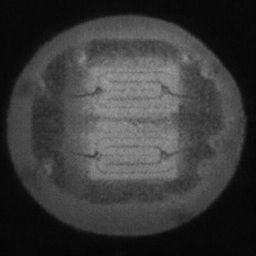
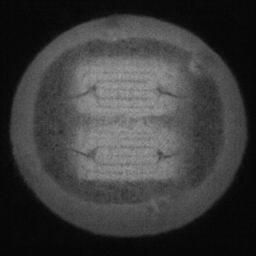
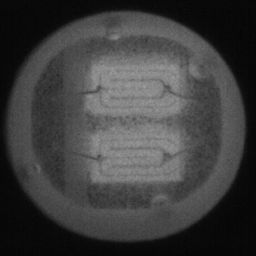
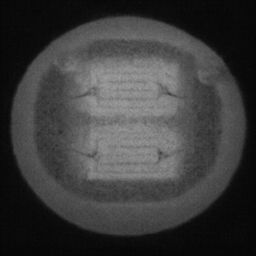
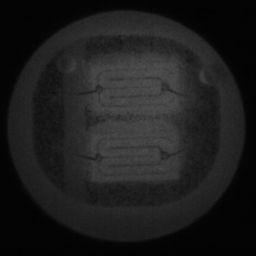
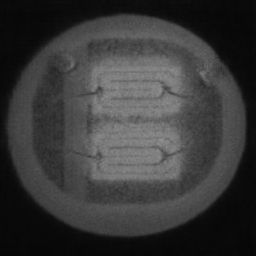
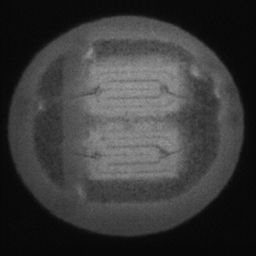
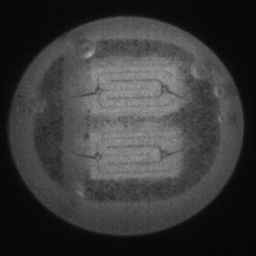
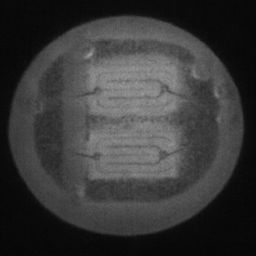
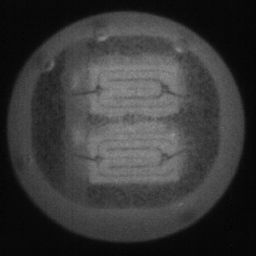
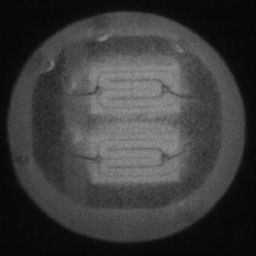
  如图4.9、图4.10与图4.11所示，DCGAN、CycleGAN与WGAN-GP各基于1098数据集训练后所生成的LED缺陷芯片图像和原始缺陷芯片图像的比较，因DCGAN和WGAN-GP的输入为随机噪声及LED缺陷芯片图像，缺乏缺陷区域的条件约束，故生成图像与原始图像的缺陷位置差距较远。从生成图像的肉眼感知上看，CycleGAN生成图像同原始图像对比背景色彩和纹理较为接近，但气泡缺陷极其模糊，人眼难以观察到其存在，DCGAN生成的LED缺陷图像具有明显的棋盘状纹理，这是由于采用了多层卷积神经网络导致的，WGAN-GP生成的缺陷图像背景与原始图像明显不符。这三个模型的生成图像均具有缺陷区域失真、几何形状不连续的问题，而CDS-GAN所生成的LED缺陷芯片不仅视觉效果逼真，且气泡缺陷辨识度高、几何形状真实，这充分说明了本文模型较之其他GANs在合成工业芯片缺陷上的优越性。

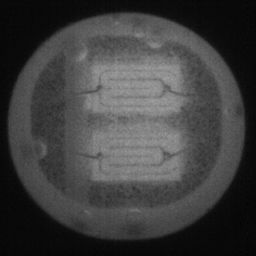
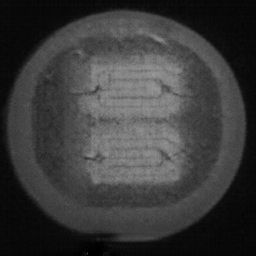
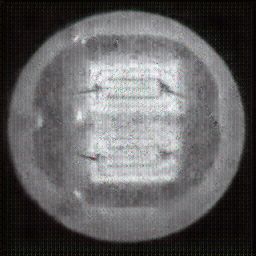
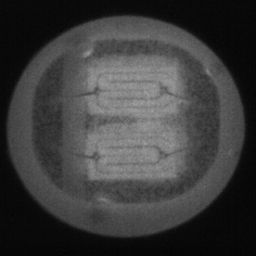
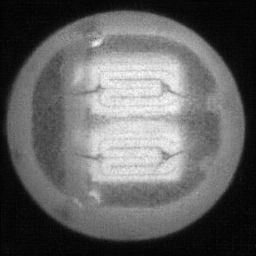
  2）定量评估

  本文使用66数据集、792数据集和1098数据集对CDS-GAN与Pix2Pix GAN进行训练测试，所得实验结果如表4.4所示。从表4.4可看出，本文所提出的CDS-GAN在66和792两个LED缺陷芯片数据集上，FID对比Pix2Pix GAN无明显优势，但CDS-GAN所生成缺陷芯片图像的SSIM与PSNR指标较之Pix2Pix GAN均有小幅提升。需要引起注意的是，CDS-GAN及Pix2Pix GAN在66数据集上都迭代训练了300个epoch，但对应的FID仍远高于792与1098数据集，这说明在训练数据集规模甚小的情况下，单纯地提高模型迭代次数无法有效提升算法性能。

  更进一步地，本文在规模更大的LED芯片缺陷图像数据集1098上对CDS-GAN以及其他GANs做模型训练，实验结果如表4.4所示。表4.4的内容显示本文方法CDS-GAN所生成图像FID值较之其他GANs都有显著降低，并且SSIM与PSNR亦与最高值不相上下。考虑到FID是比SSIM与PSNR更好的反映图像翻译、图像重构的指标，故CDS-GAN的数据增强效果要强于其他GANs，目标检测的结果也对此做了有力证明。值得一提的是，1098数据集是66数据集和792数据集的超集，而CDS-GAN在前者的表现明显优于Pix2Pix GAN，在后两个数据集上无法充分展示CDS-GAN的优越性，这也表明与目标检测任务类似，数据增强也对样本的质量与数量有一定要求。

  为了表明同其他GANs相比，CDS-GAN 合成缺陷芯片图像的效果最佳，本文基于1098数据集对Pix2Pix GAN、CycleGAN、DCGAN 和 WGAN-GP 做了横向对照，如表 4.5 所示，实验结果表明CDS-GAN 生成的LED缺陷芯片相似度最高、特征最丰富。

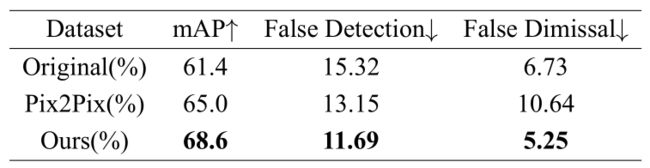
  提升目标检测性能是进行数据增强的最终落脚点，因此本文将CDS-GAN、Pix2Pix GAN基于1098数据集生成的缺陷芯片图像分别用于扩增原始数据集，再用两个扩增数据集与原始数据集来训练SSD算法完成目标检测任务。SSD模型训练超参数的设置如表4.6所示，所用训练数据与测试数据的样本数量设置如表4.7所示，其中总的原始LED缺陷芯片图像198张，向其中分别添加1098张生成的LED缺陷芯片图像得到两个扩增数据集，每个数据集按6:4:4的比例划分train、val、test集，用作训练、验证和测试。最终的缺陷检测结果如表4.8所示，CDS-GAN所生成图像对提升分类器的效果十分显著。

  图4.12更为直观地呈现原始数据集、Pix2Pix GAN扩增数据集、CDS-GAN扩增数据集训练得到的SSD检测效果的差异，每一行从左至有依次为应用三个数据集对SSD进行训练所得的测试结果图。通过图4.12 d）与图4.12e对比，以及图4.12 g）与图4.12 h）比对，可以发现Pix2Pix GAN扩增数据集不仅未成功完成数据增强的预期目标，反而使SSD产生了更多的漏检，这也与表4.8的结果一致。Pix2Pix GAN生成的缺陷图像与目标图像的逼真度不足，导致SSD检测器学习到了赘余的无效特征，从而无法准确预测缺陷，这是其漏检缺陷数量增多的主要原因。

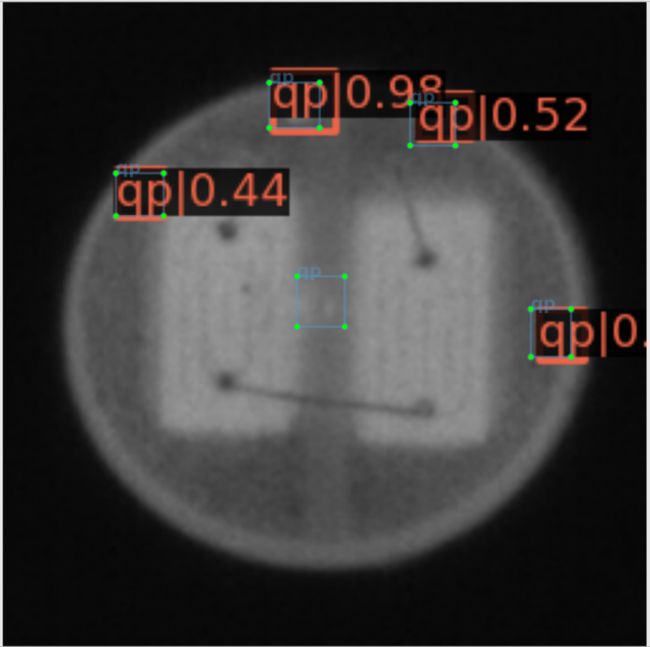
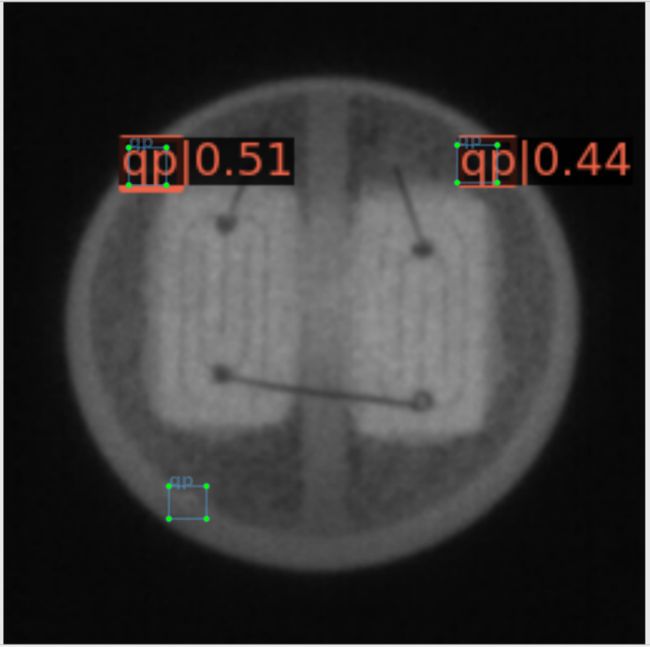
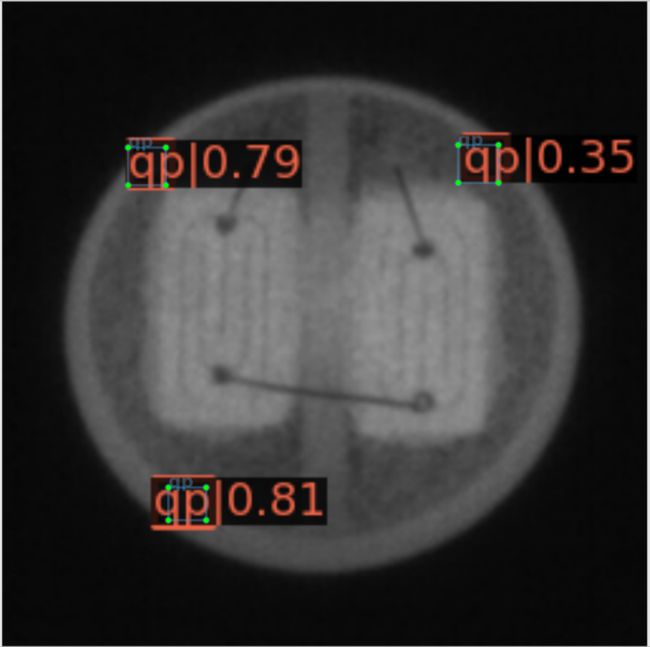
  需要注意的是，图4.12所示的全部图像图像均为真实的缺陷图像，即图4.12表达的含义是试图使用数据增强的方法优化SSD检测器所取得的实际结果与原始结果的对比。在数据集的真实样本以外为生成样本，CDS-GAN与Pix2Pix GAN合成的缺陷图像也作为数据集的一个子集，更是对各项指标的计算都产生影响，因此将SSD检测器对其测试结果进行展示是有必要的，如图4.13所示。由于真实缺陷图像是SSD检测器训练数据的一部分，且不论CDS-GAN或Pix2Pix GAN，两者生成图像都是以真实缺陷图像的数据分布空间为目标域，因此SSD检测器所学习到的能力必将是整体偏向预测真实缺陷或与之类似的图像区域。通过图4.13展示的结果，Pix2Pix GAN生成图像不仅会造成SSD检测器漏检，且误检的概率也比基于CDS-GAN生成图像的要高，表4.8对此给出了定量评估，再结合SSD检测器的学习源，可以判定CDS-GAN比Pix2Pix GAN更适合工业缺陷芯片的数据增强任务。

GPP芯片图像数据集

  GPP缺陷芯片图像一共包含3个数据集，依次是80数据集、560数据集与1040数据集。在GPP缺陷芯片数据集上的操作同LED缺陷芯片数据集的相似，本文用80数据集和560数据集分别训练CDS-GAN与Pix2Pix GAN，而1040数据集被用于训练CDS-GAN及Pix2Pix GAN、CycleGAN、DCGAN、WGAN-GP，用于训练的GPP缺陷芯片-mask图像对如4.14所示，本文也从定性与定量两方面分析了GPP数据集上的实验结果。作为对比参照，在使用80数据集进行训练时，CDS-GAN、Pix2Pix GAN的n_epochs与n_epochs_decay分别取150。

  1）定性评估

  如图4.15、图4.16与图4.17所示，CDS-GAN和Pix2Pix GAN各基于80数据集、560数据集、1040数据集训练后所生成的GPP缺陷芯片图像与原始缺陷芯片图像的对比。从人眼主观上观察，不论CDS-GAN或Pix2Pix GAN，生成的GPP缺陷图像与原始缺陷图像存在明显差异，背景覆盖着一层"膜"，整体较为模糊，且生成缺陷与原始缺陷的位置和形状较之LED芯片没有严格对应，本文从理论上分析：这是由于GPP的缺陷没有被mask精确覆遮导致的。

  如图4.18、图4.19与图4.20所示，DCGAN、CycleGAN与WGAN-GP各基于1040数据集训练后所生成的GPP缺陷芯片图像和原始缺陷芯片图像的对比。CycleGAN生成图像与Pix2Pix GAN的相差无二，而DCGAN、WGAN-GP因生成器和判别器都采用了多层深度卷积网络，故生成缺陷图像含有大量显著的棋盘状纹理，此外WGAN-GP的生成图像边缘嵌入了未知的阴影。

结论与展望

参考文献

[1]王鹏飞. 中国集成电路产业发展研究[D]. 武汉: 武汉大学, 2014.

[2]徐彩云. 我国高端芯片困境的成因与突破——华为经验[D]. 成都: 西南财经大学, 2019.

[3]韩慧. 基于深度学习的工业缺陷检测方法研究[D]. 重庆: 重庆邮电大学, 2019.

[4]郭怀勇. 柔性IC封装基板外观缺陷检测问题研究[D]. 广州: 华南理工大学, 2020.

[5]吴晓元. Mask R-CNN对工业CT图像缺陷的检测和分割[D]. 兰州: 兰州交通大学, 2020.

[6]路浩. 基于机器视觉的碳纤维预浸料表面缺陷检测方法的研究[D]. 济南: 山东大学, 2020.

[7]Ryosuke Nakajimaa, Ryuta Nakamurab, Takuya Hidab, Toshiyuki Matsumotob. Effect of bright and shade, and luminance difference of defect on defect detection in appearance inspection utilizing peripheral vision[J]. International Journal of Industrial Ergonomics, March 2021, Volume 82, 1-11.

[8]Maike Stern, Martin Schellenberger. Fully convolutional networks for chip-wise defect detection employing photoluminescence images: Efficient quality control in LED manufacturing[J]. Journal of Intelligent Manufacturing, 2021, 32(10), 113-126.

[9]封学勇. 基于深度学习的柱形锂电池钢壳表面缺陷识别与分类方法[D]. 合肥: 合肥工业大学, 2020.

[10]Ruzlaini Ghoni, Mahmood Dollah, Aizat Sulaiman, Aizat Sulaiman, Fadhil Mamat Ibrahim. High Speed Track Defect Detection Methods Based on Enhanced Magnetic Field Eddy Currents[J]. Advances in Mechanical Engineering, 2014, Volume 2014, 1-11.

[11]南晓虎, 丁雷. 深度学习的典型目标检测算法综述[J]. 计算机应用研究, 2020, 37(S2), 15-21.

[12]李彦冬, 郝宗波, 雷航. 卷积神经网络研究综述[J]. 计算机应用, 2016, 36(06), 2508-2565.

[13]I.Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, B. Xu, David Warde-Farley, S. Ozair, Aaron C. Courville, Yoshua Bengio. Generative Adversarial Networks[J]. Advances in Neural Information Processing Systems, 2014, Volume 2014, 1-9.

[14]Hung-Yu Tseng, Lu Jiang, Ce Liu, Ming-Hsuan Yang, Weilong Yang. Regularizing Generative Adversarial Networks under Limited Data[C]. CVPR 2021, 2021, Volume 2021, 1-11.

[15]Baris Gecer, Stylianos Ploumpis, Irene Kotsia, Stefanos Zafeiriou. GANFIT: Generative Adversarial Network Fitting for High Fidelity 3D Face Reconstruction[C]. CVPR 2019, Volume 2019, 1155-1164.

[16]Zhewei Huang, Wen Heng, Shuchang Zhou. Learning to Paint With Model-based Deep Reinforcement Learning[C]. ICCV 2019, Volume 2019, 8709-8718.

[17]Zilong Huang, Xinggang Wang, Yunchao Wei, Lichao Huang, Humphrey Shi, Wenyu Liu, Thomas S. Huang. CCNet: Criss-Cross Attention for Semantic Segmentation[C]. ICCV 2019, Volume 2019, 603-612.

[18]Dario Pavllo, Graham Spinks, Thomas Hofmann, Marie-Francine Moens, Aurelien Lucchi. Convolutional Generation of Textured 3D Meshes[C]. NeurIPS 2020, Volume 2020.

[19]Ajil Jalal, Liu Liu, Alexandros G. Dimakis, Constantine Caramanis. Robust compressed sensing of generative models[C]. NeurIPS 2020, Volume 2020.

[20]Zhizhong Han, Chao Chen, Yu-Shen Liu, Matthias Zwicker. ShapeCaptioner: Generative Caption Network for 3D Shapes by Learning a Mapping from Parts Detected in Multiple Views to Sentences[C]. ICML 2020, Volume 2020.

[21]Chen Gao, Si Liu, Defa Zhu, Quan Liu, Jie Cao, Haoqian He, Ran He, Shuicheng Yan. InteractGAN: Learning to Generate Human-Object Interaction[C]. ACM 2020, Volume 2020.

[22]Jianwen Xie, Yang Lu, Ruiqi Gao, Song-Chun Zhu, Ying Nian Wu. Cooperative Training of Descriptor and Generator Networks[C]. ACM 2016, Volume 2016.

[23]Adam Polyak, Yaniv Taigman, Lior Wolf. Unsupervised Generation of Free-Form and Parameterized Avatars[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, Volume 42, 444-459.

[24]Zhedong Zheng, Yi Yang. Unsupervised Scene Adaptation with Memory Regularization in vivo[J]. International Joint Conference on Artificial Intelligence, Volume 2020.

[25]Ceyuan Yang, Yujun Shen, Bolei Zhou. Semantic Hierarchy Emerges in Deep Generative Representations for Scene Synthesis[J]. International Joint Conference on Artificial Intelligence, Volume 2019.

[26]Zhenliang He, Wangmeng Zuo, Meina Kan, Shiguang Shan, Xilin Chen. AttGAN: Facial Attribute Editing by Only Changing What You Want[J]. IEEE Trans Image Process, 28(11), 5464-5478.

[27]Faming Fang, Juncheng Li, Juncheng Li, Tieyong Zeng, Tieyong Zeng. Soft-edge Assisted Network for Single Image Super-Resolution[J]. IEEE Transactions on Image Processing, PP(99), 2020.

[28]Mehdi Mirza, Simon Osindero. Conditional Generative Adversarial Nets[J]. arXiv:1411.1784, 2014.2.

[29]刘建伟, 谢浩杰, 罗雄麟. 生成对抗网络在各领域应用研究进展[J]. 自动化学报, 46(12), 2020, 2500-2536.

[30]A.Krizhevsky, Ilya Sutskever, Geoffrey E. Hinton. ImageNet classification with deep convolutional neural networks[C]. NIPS, Volume 2012.

[31]Hazael serrano guerrero, C. Cruz-Hernández, Rosa Martha Lopez-Gutierrez, Rosa Martha Lopez-Gutierrez, R.A. ChávezPérez. Chaotic Synchronization in Nearest-Neighbor Coupled Networks of 3D CNNs[J]. Journal of Applied Research and Technology, 11(1), 26-41.

[32]S. Kiranyaz, T. Ince, M. Gabbouj. Real-Time Patient-Specific ECG Classification by 1-D Convolutional Neural Networks[J].

[33]IEEE Transactions on Biomedical Engineering, Volume 2016.

[34]Liu Yao; Pu Hongbin; Sun Da-Wen. Efficient extraction of deep image features using convolutional neural network (CNN) for applications in detecting and analysing complex food matrices[J]. Trends in Food Science & Technology, Volume 113, 2021, 193-204.

[35]Alec Radford, Luke Metz, Soumith Chintala. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks[C]. ICLR, 2016.

[36]Sang Van Doan, Thien Huynh-The, Dong-Seong, KimDong-Seong Kim. Underwater Acoustic Target Classification Based on Dense Convolutional Neural Network[J]. IEEE Geoscience and Remote Sensing Letters, PP(99), 2020, 1-5.

[37]Martin Arjovsky, Soumith Chintala, L´eon Bottou. Wasserstein GAN[C]. ICML, 2017.

[38]Jun-Yan Zhu, Taesung Park, Phillip Isola, Alexei A. Efros. Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks[J]. ICCV, 2017.

[39]彭鹏. 基于CycleGAN的图像风格转换[D]. 成都: 电子科技大学, 2019.

[40]Phillip Isola, Jun-Yan Zhu, Tinghui Zhou, Alexei A. Efros. Image-to-Image Translation with Conditional Adversarial Nets[C]. IEEE Conference on Computer Vision and Pattern Recognition, Volume 2017, 5967 - 5976.

[41]杜虎强. 基于生成对抗网络的晶圆扫描电镜图像生成研究[D]. 杭州: 浙江大学, 2020.

[42]张晋, 谢珺, 梁凤梅, 续欣莹, 董俊杰. 一种改进DCGANs网络的磁瓦缺陷图像生成方法研究[J]. 小型微型计算机系统, 42(03), 2021, 589-594.

[43]谢源, 苗玉彬, 许凤麟, 张铭. 基于半监督深度卷积生成对抗网络的注塑瓶表面缺陷检测模型[J]. 计算机科学, 47(07), 2020, 92-96.

[44]刘坤, 文熙, 黄闽茗, 杨欣欣, 毛经坤. 基于生成对抗网络的太阳能电池缺陷增强方法[J]. 浙江大学学报(工学版), 54(04), 2020, 684-693.

[45]Gongjie Zhang, Kaiwen Cui, Tzu-Yi Hung, Shijian Lu. Defect-GAN: High-Fidelity Defect Synthesis for Automated Defect Inspection[C]. WACV, 2021.

[46]Liu Juhua, Wang Chaoyue, Su Hai, Du Bo, Tao Dacheng. Multistage GAN for Fabric Defect Detection[J]. IEEE Transactions on Image Processing, 2019.

[47]Hui Lin. Defect Image Sample Generation With GAN for Improving Defect Recognition[J]. IEEE Transactions on Automation Science and Engineering PP(99), 2020, 1-12.

[48]Tu Dinh Nguyen, Trung Le, Hung Vu, Dinh Phung. Dual Discriminator Generative Adversarial Nets[C]. NIPS, 2017.

[49]Oliver Rippel, Maximilian Muller, Dorit Merhof. GAN-based Defect Synthesis for Anomaly Detection in Fabrics[C]. ETFA, 2020.

[50]Kullback, S., and Leibler, R. A… On information and sufficiency[J]. The Annals of Mathematical Statistics, 22(1), 1951, 79–86.

[51]Jianhua Lin. Divergence measures based on the Shannon entropy. IEEE Transactions on Information theory, 37(1), 1991, 145–151.

[52]O. Ronneberger, P. Fischer, and T. Brox. U-net: Convolutional networks for biomedical image segmentation[C]. MICCAI, 2015.

[53]余兴建, 舒伟程, 胡润, 谢斌, 罗小兵. 高出光品质LED封装:现状及进展[J]. 中国科学:技术科学, 2017,47(09), 891-922.

[54]陈奇. 大功率LED封装热可靠性与寿命预测研究[D]. 武汉: 华中科技大学, 2018.

[55]Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun. Deep Residual Learning for Image Recognition[C]. CVPR, 2016.

[56]Han Zhang, Ian Goodfellow, Dimitris Metaxas, Augustus Odena. Self-Attention Generative Adversarial Networks[C]. arXiv:1805.08318v2, 2019.

[57]林少文. 基于生成对抗网络的人脸图像修复算法研究[D]. 广州: 华南理工大学, 2019.

[58]晁杰. 基于生成对抗网络的图像超分辨率重建[D]. 徐州市: 中国矿业大学, 2020.

[59]于文家, 丁世飞. 基于自注意力机制的条件生成对抗网络[J]. 计算机科学, 48(01), 2021, 241-246.

[60]Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift[C]. In International Conference on Machine Learning, 2015, 448-456.

[61]Abien Fred Agarap. Deep Learning using Rectified Linear Units (ReLU)[J]. arXiv:1803.08375, 2018.

[62]Neverova N, Wolf C, Taylor G W, Nebout F. Multiscale deep learning for gesture detection and localization[C]. In European Conference on Computer Vision Workshops. Zurich, Switzerland, 2014, 474-490.

[63]Hariharan B, Arbelaez P, Girshick R, Malik J. Hypercolumns for object segmentation and fine-grained location[C]. Preceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 2015, 447-456.

[64]Pierre Sermanet, Soumith Chintala, Yann LeCun. Convolutional neural networks applied to house numbers digit classification[C]. Proceedings of the 21st International Conference on Pattern Recognition, 2012.

[65]Farabet C, Couprie C, Najman L, Lecun Y. Learning hierarchical feature for scene labeling[C]. IEEE Transaction on pattern analysis and machine intelligence, 35(8), 2013, 1915-1929.

[66]Saining Xie, Zhuowen Tu. Holistically-Nested Edge Detection[C]. Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 2015, 1395-1403.

[67]Nikita Jaipuria, Shubh Gupta, Praveen Narayanan, Vidya N. Murali. On the Role of Receptive Field in Unsupervised Sim-to-Real Image Translation[J]. arXiv:2001.09257, 2020.

[68]Karen Simonyan, Andrew Zisserman. Very Deep Convolutional Networks for Large-Scale Image Recognition[J]. arXiv:1409.1556v4, 2015.

[69]Wei Liu, Dragomir Anguelov, Dumitru Erhan, Christian Szegedy, Scott Reed, Cheng-Yang Fu, Alexander C. Berg. SSD: Single Shot MultiBox Detector[J]. arXiv:1512.02325, 2016.

[70]Diederik Kingma, Jimmy Ba. Adam: A Method for Stochastic Optimization[J]. arXiv:1412.6980v5, 2014.

[71]Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, Günter Klambauer, Sepp Hochreiter. GANs Trained by a Two Time-Scale Update Rule Converge to a Nash Equilibrium[J]. arXiv:1706.08500v1, 2018.

[72]Martin Arjovsky, Léon Bottou. Towards Principled Methods for Training Generative Adversarial Networks[J]. arXiv:1701.04862, 2017.

[73]Ishaan Gulrajani, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, Aaron C. Courville. Improved Training of Wasserstein GANs[C]. NeurIPS Proceedings, 2017.

【持续更新中，直到把论文搬到博客上面来为止。】