推荐系统笔记7-Neural Factorization Machines for Sparse Predictive Analytics

这篇文章介绍NFM(Neural Factorization Machines for Sparse Predictive Analytics)，Paper链接。

具体的代码实现见Github

摘要

和FNN、PNN一样，针对类别变量One-hot以后的稀疏输入，如何做交互而引出NFM，FM可以捕捉交互（二阶特征），但是以线性方式；DNN可以捕捉非线性特征交互，如Wide & Deep，但同时深度结构使得网络不好训练；所以文章提出NFM（FM+NN），比FM要好7.3%？且结构更浅。

一、介绍

对于预测分析，比如信息检索、推荐、计算广告等，特征大多是离散和类别型的，可以将其映射为One-hot向量，然后用LR和SVM模型来处理。但是这样子会使得特征矩阵高维且稀疏，所以特征交互是一个繁杂的问题，大多是人工设计，比如（银行职员，医生）和（男，女）可以组合起来，但这样做成本过高；
所以另一种方式是从ML模型中自动学习，比如FM，将特征映射到Embedding向量，特征之间的交互通过内积来实现，但是FM仅限二阶交互；NFM可实现高阶交互+非线性特征交互；其通过设计一个新的NN中的操作-双线性交互（Bi-Interaction）池化，且这个池化层可以加深较浅的线性FM，从而提取高阶和非线性特征交互；这里提一下：FNN对于Embedding向量直接拼接起来；PNN不仅拼接，也包含另外的内积和外积操作；而这里的NFM是以Bi-Interaction来实现对于Embedding的处理。

二、MODELLING FEATURE INTERACTIONS

用GBDT手工提取组合特征会导致泛化性不好，也就是训练集没有，但是测试集有，且成本高；所以通过Embedding向量将稀疏输入映射到低微稠密空间可以泛化没有见过的特征组合，不论是什么领域，都可以将方法归为两类：1、基于FM的线性模型；2、基于NN的非线性模型。

2.1、Factorization Machines

FM是为推荐系统而提出的，其公式如下：

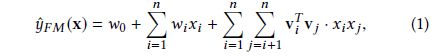
$w_0$是全局偏差，$v_i^T{v}_j$代表因子交互，但是因为系数$x_i{x}_j$，所以只会考虑非0的特征向量；FM的一个强大之处在于其泛化性，但是因为FM属于多元线性模型，但是现实中的数据是非线性的且不能由线性模型精确的表示，所以FM能力不足；那么如何实现非线性建模呢？NFM通过二阶特征隐藏向量的非线性变换来实现；

2.2、 Deep Neural Networks

一开始不知如何使用DNN来处理稀疏数据，后面一些研究陆续展开：neural collaborative filtering (NCF) frameword 来学习用户和物品的交互；后面又产生了attribute-aware CF；还有前几篇文章的FNN、Wide & Deep等；这些模型是通过拼接多个Embedding层来学习特征交互；
作者认为这种简单的拼接只提取了很少的低层次信息，所以为了解决这个问题，需要使用多层NN来实现，但是多层NN很难最优化参数，会出现梯度消失/爆炸、过拟合等问题；举个例子说明一下这个最优化参数难点，如下图所示：

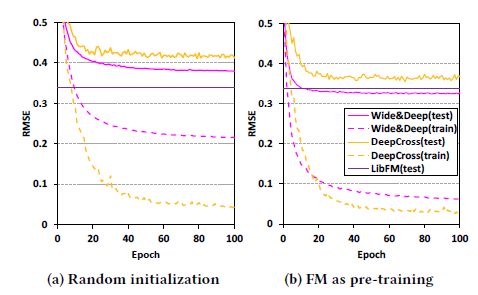
发现用FM来进行预训练会使得效果提升大约11%。

三、NEURAL FACTORIZATION MACHINES

3.1 The NFM Model

和FM类似，给定$\mathrm{x}\in R^N$，其预测公式为：$${\hat{y}}_{NFM}(x)=w_0+\sum _{i=1}^n{w}_i{x}_i+f(x)$$也就是和FM不同的在于第三部分$f(x)$，这也是NFM的核心部分，其结构如下图所示：

下面逐层介绍NFM：
Embedding layer: 这里是一个全连接层，将稀疏输入映射到一个密集向量；假设$v_i\in R^k$代表第i个特征的Embedding向量，在Embedding后，得到全部向量$$V_x=\{x_1{v}_1,...,x_n{v}_n\}$$用这个来重新表示输入x；
Bi-Interaction Layer: 是一个池化操作，将一系列的Embedding向量转换为一个向量，如下所示：$$f_{BI}(V_x)=\sum _{i=1}^n\sum _{j=i+1}^n{x}_i{v}_i\odot x_j{v}_j$$其中$\odot$代表逐个元素对应相乘，所以函数f的输出是一个k维向量，其作用是编码了二阶特征的交互；
作者提出NFM模型的Bi-Interaction层不引入新的参数，且可以在常数时间内计算完成；为了证明可以在线性时间内完成交互，将上式重写如下：

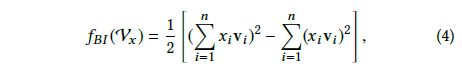
从上式可以看出，时间复杂度是$O(k{N}_x)$，其中$N_x$代表非零输入x，这意味着Bi-Interaction层不带来额外的成本增加；
Hidden Layers： 这层就是NN，所做内容如下，具体不做介绍了，不是很难：

Prediction Layer: 输出得分定义为$f(x)=h^T{z}_L$，其中h代表神经元权重，综上我们得到了$f(x)$的定义，NFM模型重写为：

所有的模型参数为$\theta =(w_0,(w_i,v_i),h,(w_l,b_l))$，NFM和FM相比，增加的参数也就是NN层的$(w_l,b_l)$；

3.1.1 NFM Generalizes FM

将NFM的全连接层去掉，直接连接输出层，得到如下计算公式：
$${\hat{y}}_{NFM}(x)=w_0+\sum _{i=1}^n{w}_i{x}_i+h^T\sum _{i=1}^n\sum _{j=i+1}^n{x}_i{v}_i\odot x_j{v}_j$$进一步重写为$${\hat{y}}_{NFM}(x)=w_0+\sum _{i=1}^n{w}_i{x}_i+\sum _{i=1}^n\sum _{j=i+1}^n\sum _{f=1}^k{h}_f{v}_{if}{v}_{jf}\cdot x_i{x}_j$$
从上式可以看出，将h置为常量$(1,...,1)$，就和FM的公式是一样的，这就将FM在NN的框架下表示出来了（注意这里的内积和PNN中的内积存在不同，具体查看上一篇介绍PNN的文章）；

3.2 Learning

首先我们需要确定一个目标函数，对于回归问题的目标函数通常为平方误差：$$L_{reg}=\sum _{x\in X}{(\hat{y}(x)-y(x))}^2$$ 一般SGD算法被用来更新参数，如下所示：

文中使用mini-batch Adagrad算法作为最优化方法，这个方法的好处是学习速率在训练阶段可以自适应调整，简化了选择一个合适的学习速率问题并更快收敛；

3.2.1、Dropout

使用Dropout来进行正则化，避免过拟合（bagging的思想），文中使用Dropout在Bi-Interaction层，在得到输出的k维向量后，随机丢弃$\rho$（Dropout ratio）个隐层向量，这也可以看作是对FM做正则化的方式；同时Dropout也应用在全连接层防止过拟合。

3.2.2 Batch Normalization

训练多层神经网络会导致协方差偏移，意味着在训练的时候每层的输入分布是会改变的，且后面层需要对这个改变做出调整，降低了训练速度，因此提出了BN；同样，BN也用在Bi-Interaction层后和全连接层上；

4 EXPERIMENTS

仿真使用的数据集是Frappe 和 Movie Lens；且和LibFM、HOFM、Wide & Deep和DeepCross（用多层ResNet训练拼接的Embedding向量）做对比；除此之外，1、训练速率从[0.005， 0.01，0.02， 0.05]中选择，2、使用AdaGrad方法，3、使用EarlyStoping，即如果4个epoch后在验证集上RMSE增加了，那么停止训练，4、Embedding维度设为64；
比较BN+Dropout（一个有趣的方向，可以减少验证集误差），如图所示：

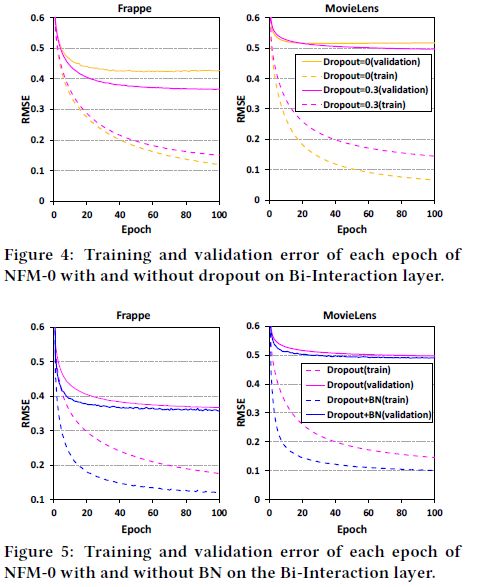
所以，NFM模型不包括全连接层的话，就是一个FM模型，但是是从NN角度来考虑的，可以加入Dropout和BN操作，从而使得模型更好；
下面考虑不同NN隐藏层的个数对结果的影响，如下所示：

从图中可以看出，1个隐藏层是最好的，原因：因为Bi-Interaction已经足够好的提取了二阶特征交互，所以只需要一个隐藏层即可；最终不同模型的对比如下：

有一个疑问，Deep Cross为啥这么差？
作者总结了几点：1、NFM是除了FM以外参数最少的，且训练效果最好，和Wide & Deep对比，间接说明了Bi-Interaction的作用；2、FM和NFM对比，说明了NN层的作用；3、Deep Cross最差表明了更深的网络结构未必最好（10层）。。。

注：以上图片均来自于原文