数据结构-归并排序
1,归并排序
1.1,归并排序思想
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。归并排序是一个典型的一空间换取时间的排序方法,是一种稳定的排序算法
- 排序过程
- 将n个元素从中间切开,分成两部分。(左边可能比右边多1个数)
- 将步骤1分成的两部分,再分别进行递归分解。直到所有部分的元素个数都为1。
- 从最底层开始逐步合并两个排好序的数列。
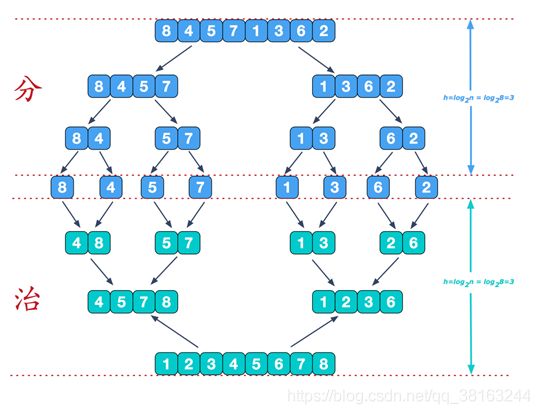
1.2,归并排序的过程
-
在归并排序中,我们需要思考两个问题,既然归并排序的思想是分治法,那么肯定有划分数据和合并数据的方法。
-
数据的合并过程
- 归并排序过程
- 归并排序总的过程
可以看到这种结构很像一棵完全二叉树,本文的归并排序我们采用递归去实现(也可采用迭代的方式去实现)。分阶段可以理解为就是递归拆分子序列的过程。
1.3,归并排序时间复杂度分析
- 归并的时间复杂度分析:主要是考虑两个函数的时间花销,
- 数组划分函数 merge();
- 有序数组归并函数mergeSorted();
- merge()函数的时间复杂度为O(n),因为代码中有2个长度为n的循环(非嵌套),所以时间复杂度则为O(n);
- 简单的分析下元素长度为n的归并排序所消耗的时间 T[n]:调用merge()函数划分两部分,那每一小部分排序好所花时间则为T[n/2],而最后把这两部分有序的数组合并成一个有序的数组mergeS()函数所花的时间为O(n);
- 公式:T[n] = 2T[n/2] + O(n); 因为不管元素在什么情况下都要做这些步骤,所以花销的时间是不变的,所以该算法的最优时间复杂度和最差时间复杂度及平均时间复杂度都是一样的为:O(nlogn )
- 因为在归并有序序列的过程中使用了一个大小是N的数组,所以归并排序的空间复杂度是O(N)。
- 数组初始序列对归并排序没有影响。
1,二路归并排序设计思路
与快速排序一样,归并排序也是基于分治策略的排序,(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。归并排序将待排序的元素分成两个长度相等的子序列,分别为每一个子序列排序,然后把子序列合并成一个总的序列。合并两个子序列的过程称为二路归并。(注:二路归并算法是一种稳定排序算法,他的运行时间不依赖与待排元素的初始序列,因此也就避免了快速排序最差的情况),算法时间复杂度![]() ,空间复杂度
,空间复杂度![]()
1.1,归并排序的递归算法:
void MergeSort(int *arr, int left, int right)
{
//left和right是当前参加归并的元素下标
if (left < right)
{
int mid = (right + left)/2;
MergeSort(arr, left, mid);
MergeSort(arr, mid + 1, right);
Merge(arr, left, right, mid);
}
}
void Merge(int *arr, int left, int right, int mid)
{
//arr[left......mid]和arr[mid+1.........right]是两个有序表将这两个表合并成一个有序表,先暂时放在array数组中,再重新放回原来的位置
int i = left, j = mid + 1, k = 0, s = right - left + 1;//i和j是检测指针,k是存放指针
int *array = new int[s];
while (i <= mid && j <= right)//如果两个表都没检测完,则两两比较
{
if (arr[i] <= arr[j])
array[k++] = arr[i++];
else
array[k++] = arr[j++];
}
while (i <= mid)//第一个表没有检测完
{
array[k++] = arr[i++];
}
while (j <= right)//第二个表没有检测完
{
array[k++] = arr[j++];
}
for (int i = 0;i < s;i++)
arr[left + i] = array[i];
free(array);
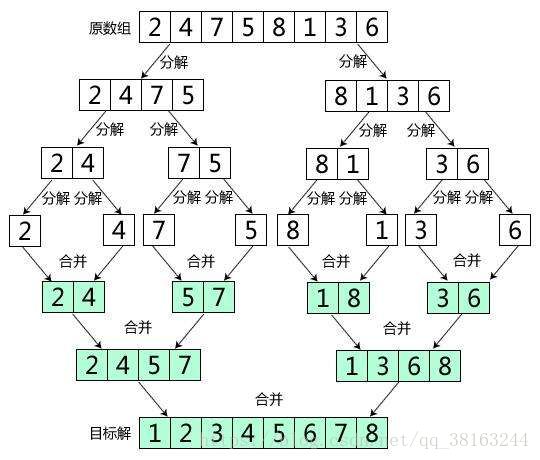
}我们可以把分解的过程理解为建立完全二叉树的过程(递归深度是![]() )
)
在这里给大家列出(2,4,7,5,8,1,3,6)这个序列归并排序的过程,从图中我们可以看到,每次都是在原有元素的基础上面对半分,即取一半,直到分解为每一组元素剩下一个为止,我们默认一个元素已经有序,然后在依次把每两个元素合并成一个有序序列,即上图中的第一步合并操作,从那里我们可以看到现在已经合并为四个分组,每个分组里面两个元素有序排列,接着在进行一次合并,合并为两个分组,每组四个元素有序排列,接着进行最后一次合并操作,整个序列变为有序,排序结束。
1.2,二路归并排序迭代算法
但是在实际上递归的归并排序时间代价和空间代价都很高,应为要做多次递归调用,最多需要![]() 的辅助数组,还需要一个规模为
的辅助数组,还需要一个规模为![]() 的递归工作站,实用性最好的是迭代的归并排序,算法是利用二路归并过程的自底向上进行排序,假设待排元素有n个,迭代的归并排序也需要一个与待排序序列一样大的可容纳n个元素的辅助空间。
的递归工作站,实用性最好的是迭代的归并排序,算法是利用二路归并过程的自底向上进行排序,假设待排元素有n个,迭代的归并排序也需要一个与待排序序列一样大的可容纳n个元素的辅助空间。
//归并排序的迭代算法实现
void Merge(int *arr1, int *arr2,int left, int right, int mid)
{
//arr[left......mid]和arr[mid+1.........right]是两个有序表将这两个表合并成一个有序 表,先暂时放在array数组中,再重新放回原来的位置
int i = left, j = mid + 1, k = 0, s = right - left + 1;//i和j是检测指针,k是存放指针
while (i <= mid && j <= right)//如果两个表都没检测完,则两两比较
{
if (arr1[i] <= arr1[j])
arr2[k++] = arr1[i++];
else
arr2[k++] = arr1[j++];
}
while (i <= mid)//第一个表没有检测完
{
arr2[k++] = arr1[i++];
}
while (j <= right)//第二个表没有检测完
{
arr2[k++] = arr1[j++];
}
}
void MergePass(int *arr1, int *arr2, int len,int n)
{
//对arr1中的长度为len的归并项进行一趟二路归并,结果存放于arr2的相同位置
int i = 0;
while (i + 2 * len <= n - 1)//两两归并长度为len的归并项,批处理归并长度为len的归并项
{
Merge(arr1, arr2, i, i + 2 * len - 1, i + len - 1);//arr1[i......i+len-1]与ar1[i+len.....i+2*len-1]
i = i + 2 * len;//i进到下一次两两归并的第一个归并项
}
if (i + len <= n)//特殊情况第二个归并项不足len
{
Merge(arr1, arr2, i, n - 1, i + len - 1);
}
else//特殊情况,只剩下一个归并项
for (int j = i;j <= n - 1;j++)
{
arr2[j] = arr1[j];
}
}
void MergeSort(int *arr, int n)
{
int i, len = 1;
int *arr2 = new int[n];
while (len < n)//第一趟归并令长度len为1,以后每次归并都让len变为原来2倍
{
MergePass(arr, arr2, len,n);
len *= 2;
MergePass(arr2, arr, len, n);
len *= 2;
}
}
下面我们以一个实例来演示迭代的归并排序,初始序列是(21,25,49,25*,93,62,72,08,37,16,54)在这里为了说明排序是稳定的,用了25*做对照,25和25*相对位置没有变,所以归并排序是稳定的。
len=1:21,25,49,25*,93,62,72,08,37,16,54
len=2:21 25,25* 49,62 93,08 72,16 37,54
len=4,:21 25 25* 49,08 62 72 93,16 37 54
len=8:08 21 25 25* 49 62 72 93,16 37 54
len=16:08 16 21 25 25* 37 49 54 62 72 93
当len=1时,我们把每个元素都看作归并项,归并为len=2的归并项,每一次len都增大原来的二倍。假设数组元素arr[0]到arr[n-1]已经归并为长度为len的归并项,要求再将这些归并项两两归并,归并成长度为2len的归并项,把这些归并项放在arr2的辅助数组中,如果n不是2len的整数倍,则归并完一趟,可能遇到两种情况:
(1)剩下一个长度为len的归并项和一个长度小于len的归并项,这时可以再次调用Merge函数将他们归并称为一个长度小于2len的归并项。
(2)只剩下一个归并项,长度小于或者等于len,由于没有另一个归并项与其归并,可以将直接放到arr2的辅助数组中,准备参加下一趟归并操作。
总之,迭代算法分为两部分,第一部分先对长度为len的归并项进行两两归并,直到出现上述情况之一,第二部分处理上述特殊情况。