递归（各经典例题分析）

递归

一、递归的概念及好处

程序调用自身的编程技巧称之为递归（ recursion）。递归做为一种算法在程序设计语言中被广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个个与原问题相似的规模较小的问题来进行求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说，递归需要有边界条件（约束条件）、递归前进段和递归返回段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

二、递归的缺点

递归算法解题相对常用的算法如普通循环等，运行效率较低。因此，应该尽量避免使用递归，除非没有更好的算法或者某种特定情况，递归更为适合的时候。在递归调用的过程当中系统为每一层的返回点、局部变量等开辟栈空间来存储。递归次数过多容易造成栈溢出的问题。

三、递归的两个必要条件

1. 必须存在限制条件，当不满足满足这个限制条件的时候，递归便不再继续。
2. 每次递归调用之后越来越接近这个限制条件，这才是递归的目的。

四、递归经典问题

4.1 打印问题。

接收一个整型值（无符号），按照顺序打印它的每一位。
例如：
输入：1234，输出 1 2 3 4。

1）分析思路
拿到这个题目，首先很容易想到用1234对10取模可得到4，再对123取模可以得到3，依次类推可以得到每一个数，接下来就要思考如何按顺序打印。

如果我们使用递归的思想，在取模得到4之后，打印4之前进行递归，这个时候可以得到123，并且4还没有被打印，然后再对123取模，得到3，但在打印3之前又递归，依次类推，当得到1之后，结束递归，直接打印1，递归返回，打印2，再返回，得到3，即可得到1 2 3 4，由此也可看出递归的约数条件，如果我们定义这个数为n，则约数条件为n < 10。

分析结束，就可以上手写代码。

2）代码示例

#define _CRT_SECURE_NO_WARNINGS 1

#include 

//依次打印1 2 3 4

void Print(unsigned int n)
{
     
	if (n > 10)
	{
     
		Print(n / 10);
	}
	printf("%u ", n % 10);
}

int main()
{
     
	unsigned int n = 0;
	//输入
	scanf("%u", &n);

	//打印函数
	Print(n);

	return 0;
}

运行代码结果：

3）代码分析
输入一个无符号整数后进入自定义的打印函数。

首先需要确定递归的满足约数条件为n > 10，因为当剩下一位数之后不需要再次递归，直接打印即可，这个一位数就是我们输入整数的第一个数字。

再看递归调用，调用自己所处的函数，但传过去的实参需要发生变化，因为我们的需求是得到4后需要的整数是123，所以传的实参应该是n / 10，即可在每次递归之后得到的n都少一位。

图示解析：

返回上一层后n = 12，打印结果为2，然后结束该层函数，返回上一层，n = 123，打印结果为3，再结束该层函数，返回上一层，n = 1234，打印结果为4，完成该次递归任务。

4.2 模拟strlen问题。

编写函数不允许创建临时变量，求字符串的长度。

1）分析思路
首先我们知道求字符串长度可以利用库函数，strlen，需要包含头文件，所以我们写这道题目其实就是自己写一个函数模拟实现strlen函数的功能。

那我们就需要了解strlen函数是怎样实现的，一般来说，从数组首元素地址开始访问，只要不是’\0’，计数就加一，直到访问到’\0’，计数即为字符串长度。

所以很容易写出以下代码：

#include 

//模拟实现strlen

int Count(char* p)
{
     
	int cnt = 0;
	while (*p)
	{
     
		cnt++;
		p++;
	}
	return cnt;
}

int main()
{
     
	char arr[20] = "abcdef";
	//计算字符串长度
	int ret = Count(arr);
	//输出
	printf("%d\n", ret);

	return 0;
}

利用循环可以很好的实现目的，但题目要求不允许创建临时变量，也就是不允许创建计数变量cnt，那么只能利用递归的思想解决这个问题。

因为不能创建临时变量，那么在递归的时候可以return 1加上递归函数，这样可以达到每次递归都加一，如果不满足递归条件就return 0，而每次递归将实参后移一个单元，就可以算出总共递归了多少次，等价为遇到’\0’之前有多少个字符，即可算出字符串长度。

2）代码演示

#include 

//模拟实现strlen

int my_strlen(char* p)
{
     
	if (*p)
	{
     
		return 1 + my_strlen(p + 1);
	}
	else
	{
     
		return 0;
	}
}

int main()
{
     
	char arr[20] = "abcdef";
	//计算字符串长度
	int ret = my_strlen(arr);

	//输出
	printf("%d\n", ret);

	return 0;
}

运行结果：

3）代码分析
第一次进入my_strlen函数的时候，第一个p所指的内容是a，不是’\0’，所以进行return 1 + my_strlen(p + 1)；此时在返回主函数之前先执行调用my_strlen函数，进入下一级函数调用，此时的p指向的是字符串中的b，依次类推，最后的p指向字符串中的f，再次调用my_strlen函数，然后p指向字符串中隐藏的’\0’，不符合约数条件，返回0，此时经历过6次递归，总共加了6个1和一个0，最终返回到主函数中的数字为6。

4.3 n的阶乘问题。

求n的阶乘。（不考虑溢出）

1）分析思路
n的阶乘如果利用迭代（循环）的思路写非常简单，但如果加上用递归的要求完成，我们就需要进行分析。

每次递归时传实参改为n - 1，并且在调用函数时在调用前乘上n，即可完成递归多少次就乘上多少个数，当然不能没有约数条件，否则容易出现栈溢出的现象，易于得知，约数条件为n > 0。

当然在解决实际问题的时候要注意分情况考虑，如果n <= 1，则n的阶乘结果应该是1，如果n > 1，则继续用递归实现。

或者可以记住n的阶乘的递归公式：n * Fac(n - 1)（n > 1）

2）代码演示

#include 

//递归求n的阶乘

int Fac(int n)
{
     
	if (n <= 1)
	{
     
		return 1;
	}
	else
	{
     
		return n * Fac(n - 1);
	}
}

int main()
{
     
	int n = 0;
	//输入
	scanf("%d", &n);

	int ret = Fac(n);

	//输出
	printf("%d\n", ret);

	return 0;
}

运行结果：

3）代码分析
输入一个整数表示你想要的求的数的阶乘，用ret接收阶乘函数的返回值，然后进入阶乘函数。

如果输入的数小于1，则直接返回1，如果大于1，则用n的阶乘的递归公式完成功能。

PS：如果有递归公式的问题可以直接套用递归公式，但别忘了加上约数条件，否则会造成栈堆溢出的问题。

4.4 斐波那契数问题。

求第n个斐波那契数。（不考虑溢出）

首先介绍一下什么是斐波那契数列，
斐波那契数列：
1 1 2 3 5 8 13 21 34 55 89 …
规律就是前两个数是1，从第三个数开始，第三个数是前两个数之和。

1）分析思路
首先容易想到递归时的约数条件为n > 2，因为n等于1或2返回值都为1。

在写大于2的斐波那契数时只需要调用n - 1和n - 2作为实参进行递归即可。

2）代码演示

#include 

//求斐波那契数

int Fib(int n)
{
     
	if (n <= 2)
	{
     
		return 1;
	}
	else
	{
     
		return Fib(n - 1) + Fib(n - 2);
	}
}

int main()
{
     
	int n = 0;
	//输入要查找的斐波那契数位数
	scanf("%d", &n);

	int ret = Fib(n);

	//输出
	printf("%d\n", ret);

	return 0;
}

运行结果：

3）代码分析
Fib(n - 1) + Fib(n - 2)代表第n个斐波那契数，而递归时，Fib(n - 1)会利用Fib(n - 2) + Fib(n - 3)得到，以此类推，最后由1 + 1得到的三个斐波那契数，往上叠加算出第n个斐波那契数，但这样的算法效率极低，一般不建议使用。

比如，如果我输入要求第50个斐波那契数，
运行结果如下：

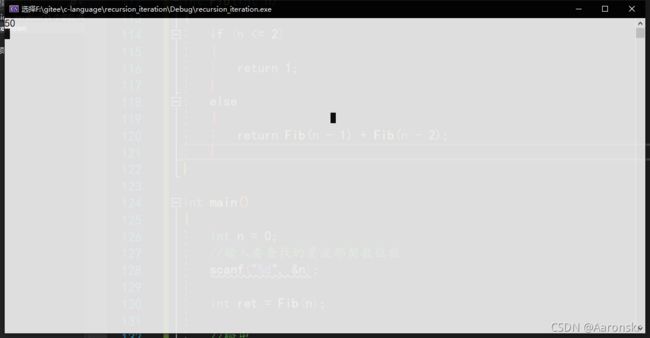
光标一直闪烁，表示代码还未结束，但是电脑cpu一直在疯狂的计算，可见效率之低，所以求斐波那契数列的问题一般不采用递归的方式去求，而是利用迭代（循环）。

4.5 汉诺塔问题。

相传在古印度圣庙中，有一种被称为汉诺塔的游戏。该游戏是在一块铜板装置上，有三根杆子（编号为A、B、C），在A杆自下而上、由大到小按顺序放置若干个金盘(如图1)。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

1）分析思路
首先，每次只能移动一个盘子，并且必须保证大盘子在下，小盘子在上，所有我们必须想办法先把最大的盘子放进C杆中，然后把第二大的盘子放进C杆中。

在这之前，我们必须利用C杆把除了最大的盘子以外的其他盘子放进B盘，然后把A杆中剩余的最大的盘子放进C杆，即完成了第一步。

再利用C盘把除了第二大的盘子以外的所有盘子由B杆移入A杆，最后再把B杆中的第二大的盘子放进C盘中，以此类推，即可完成。

2）代码实现

#define _CRT_SECURE_NO_WARNINGS 1

//汉诺塔问题

#include 

void move(char pos1, char pos2)
{
     
	printf("%c -> %c\n", pos1, pos2);
}

//a表示起始位置
//b表示中转位置
//c表示目的位置
void hanoi(int n, char a, char b, char c)
{
     
	if (1 == n)
	{
     
		move(a, c);
	}
	else
	{
     
		hanoi(n - 1, a, c, b);
		move(a, c);
		hanoi(n - 1, b, a, c);
	}
}

int main()
{
     
	int n = 0;
	//输入盘子的个数
	scanf("%d", &n);
	hanoi(n, 'a', 'b', 'c');

	return 0;
}

运行结果：

3）代码分析
首先确定n的个数，即盘子的个数（放在A杆上），然后进入hanoi函数，如果盘子的个数只有一个，直接把a中的盘子放进c盘即可，即进入move函数。

如果盘子的个数大于1，假定为n，则需要利用递归，把n - 1个盘子从A借助C放进B杆中，然后再把A中剩余的最大的盘子放进C杆中，再次利用递归把剩下的n - 1个B杆中的盘子借助A放进C。

其中hanoi函数中的形参定义的三个杆子，A表示起始位置，B表示中转位置，C表示目的位置。

4.6 青蛙跳台阶问题。

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

1）分析思路
设f（n）表示青蛙跳上n级台阶的跳法数。当只有一个台阶时，即
当n = 1时，有一种跳法；
当n = 2时，有两种跳法；
当n = 3时，有三种跳法；
当n很大时，青蛙在最后一步跳到第n级台阶时，有两种情况：

1. 第一种是青蛙在第n - 1个台阶上跳一个台阶，那么青蛙完成前n - 1个台阶，就有f（n - 1）种跳法，这是一个子问题。
2. 第二种是青蛙在第n - 2个台阶跳两个台阶到第n个台阶，那么青蛙完成前面n - 2个台阶，就有f（n - 2）种情况，这又是另外一个子问题。

而不管n的数字有多大，最后递归都会回归到n = 1或者n = 2，所以只需要在约束条件内一直递归即可。

仔细一看，其实就是著名的斐波那契数列，但是与斐波那契数列的还是有一点区别，斐波那契数列是从1开始，f（1） = 1，f（2） = 1。

或者可以记住这种题型的递推公式，f（n） = f（n - 1） + f（n - 2）。

2）代码示例

#define _CRT_SECURE_NO_WARNINGS 1

//青蛙跳台阶问题

#include 

int frog_jump(int n)
{
     
	if (n == 1 || n == 2)
	{
     
		return n;
	}
	else
	{
     
		return frog_jump(n - 1) + frog_jump(n - 2);
	}
}

int main()
{
     
	int n = 0;
	//输入台阶个数
	scanf("%d", &n);

	int ret = frog_jump(n);

	//输出
	printf("%d\n", ret);

	return 0;
}

运行结果：

3）代码分析

先确定台阶的总个数，进入frog_jump函数，如果n的个数是1或者2则可以直接return n得到结果，如果n大于3，则利用递归，在约束条件下得到每一次台阶的跳法数，然后累加得到总共第n个台阶的跳法数。

4.7 逆序字符串问题。

编写一个函数 reverse_string（char* string）（递归实现）
实现： 将参数字符串中的字符反向排列，不是逆序打印。
要求： 不能使用C函数库中的字符串操作函数。

比如：

char arr[] = " abcdef "；

结果：
fedcba

1）问题分析

逆序字符串问题，首先我们需要知道字符串的长度是多少，但因为不能使用C函数库中的字符串操作函数，所以strlen函数不能使用，但在前面已经提过模拟strlen函数的实现，所以这个问题可以轻松解决。

得到字符串长度之后，只需要将第一个字符和最后一个字符通过创建临时变量的方式将其交换即可，而最后一个字符可通过’\0’找到，然后将第一个字符指针加一，最后一个字符指针减一，然后递归即可。

2）代码演示

#include 

//逆序字符串问题

int my_strlen(char* p)
{
     
	if (*p)
	{
     
		return 1 + my_strlen(p + 1);
	}
	else
	{
     
		return 0;
	}
}

void reverse_string(char arr[], int left, int right)
{
     
	int tmp = 0;
	
	//换位置
	tmp = arr[left];
	arr[left] = arr[right];
	arr[right] = tmp;
	if (left < right)
	{
     
		reverse_string(arr, ++left, --right);
	}
}

int main()
{
     
	char arr[20] = "abcdef";
	//计算字符串长度
	int len = my_strlen(arr);

	int left = 0;
	int right = len - 1;
	//逆序字符串
	reverse_string(arr, left, right);

	//输出
	printf("%s\n", arr);

	return 0;
}

3）代码分析

首先给出字符串，这里可以写成需要控制台输入的字符数组，只需要注意数组大小的问题即可，然后就是问题分析中提到的模拟实现strlen函数的功能，利用my_strlen，在遇到’\0’之前一直递归，递归次数即代表了字符串长度。

在主函数定义left和right代表字符数组的下标，方便之后交换位置时利用数组下标进行交换，再将数组名，两个数组下标作为实参传递，在reverse_string函数内部实现交换一次，通过递归多次交换，if （lefr < right）作为约数条件，即可完成该功能。

4.8 无符号数每位求和问题。

计算一个数的每位之和。
写一个递归函数DigitSum（n），输入一个非负整数，返回组成它的数字之和。

例如：调用DigitSum（1729），则应该返回1 + 7 + 2 + 9，它的和是19。
输入：1729；
输出：19。

1）问题分析

这个题目和之前将的打印问题很相似，需要我们把一个无符号数的每一位拆下来之后，全部累加求出结果。

而拆下每一位的方法又是对其模10后除以10，对此操作，可以利用递归实现。

2）代码演示

#include 

//计算一个数的每位之和（递归实现）

typedef unsigned int uint;

int DigitSum(int n)
{
     
	static uint sum = 0;
	if (n >= 10)
	{
     
		DigitSum(n / 10);
	}
	return sum += (n % 10);
}

int main()
{
     
	uint n = 0;
	//输入一个无符号整数
	scanf("%u", &n);

	int ret = DigitSum(n);

	//输出
	printf("%u\n", ret);

	return 0;
}

运行结果：

3）代码分析

因为unsigned int比较长，而且后续使用次数较多，所以在预处理命令前先使用typedef将其改名为uint，当然后面的打印格式和输入格式全部要变成%u。

进入DigtitSum函数，首先要创建一个sum变量储存我们未来的和，但是因为每次递归会重新经过sum变量的创建，所以sum的值会被一直清0，所以定义sum变量时，应该使用static uint类型来进行定义，将sum变量设置为静态的，就不会产生bug。

然后在满足约数条件n >= 10的情况下递归n / 10，即可完成功能。

4.9 模拟pow函数问题。

编写一个函数实现n的k次方，使用递归实现。

1）问题分析

很容易的，我们知道，次方问题一般是使用库函数pow来进行实现，需要引头文件来完成，但这道题的要求是利用递归实现模拟pow函数。

也就是说我们可以通过递归调用（n - 1），然后累乘的方式完成。

2）代码演示

#include 

//递归实现n的k次方

int Fac(int n, int k)
{
     
	if (k > 0)
	{
     
		return n * Fac(n, k - 1);
	}
	else
	{
     
		return 1;
	}
}

int main()
{
     
	int n = 0;
	int k = 0;
	//输入指数和底数
	scanf("%d %d", &n, &k);

	int ret = Fac(n, k);

	//输出
	printf("%d\n", ret);

	return 0;
}

运行结果：

3）代码分析

将n设为底数，k设为指数，进入Fac函数，约束条件为k > 0，每次递归前累乘上一个n，递归调用参数为k - 1，即递归调用多少次，则累乘了多少个n，最终实现功能。

总结

以上就是本文所有内容，递归虽然并不是效率很高的算法，但确实是程序员们常用的算法，因为它具备将大事化小的能力，将复杂的问题简单化，使用时需要注意必须有约数条件，否则容易造成栈堆溢出问题。

希望本文能够对大家有帮助~