PatchMatchNet实践（环境配置、相关软件安装）及理论学习笔记（更新中）

0 概述

patchmatchNet是算比较新的用于mvs的网络，出自文章《PatchmatchNet: Learned Multi-View Patchmatch Stereo》，论文链接为：https://arxiv.org/abs/2012.01411。说起来传统的sgm方法，和深度学习结合后变成了sgm-nets，传统的双边格网加速和深度学习结合后变成了bgnets，如今传统的patchmatch和深度学习结合后就变成了patchmatchNets，近几年，将传统匹配方法的一些优化思想迁移到深度学习网络中似乎已经是一种标配，不知道将来的发展方向又会在哪里，如今且学且珍惜了。论文代码作者已经开源，地址为：
https://github.com/FangjinhuaWang/PatchmatchNet。
本文主要记录了刚入门深度学习MVS的一些过程。包括了使用patchmatchnet的demo时的一些环境配置，以及一些相关的三维重建的软件的安装，比如说meshlab、colmap等，再有，其中用到了matlab来进行一些定量的评估，因此这里也提供了matlab的安装等，本文将尽可能的复现整体探索过程，包括遇到的各种错误以及自己的解决方式和理解等等。此外，在配完环境，跑通patchmatchnet后，则一步一步的进去阅读其核心源码，和论文对照着进行理解，当我遇到一些pytorch或者python的知识点时，也会额外进行记录。

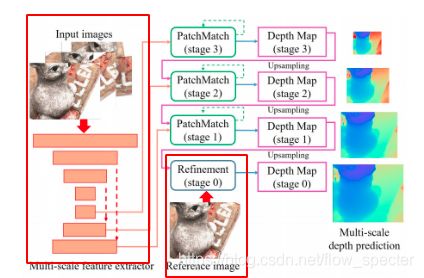
Patchmatch-Net的整体网络结构以及基于学习的patchmatch如以下的两幅图所示，这将贯穿全文，起指导性的作用。

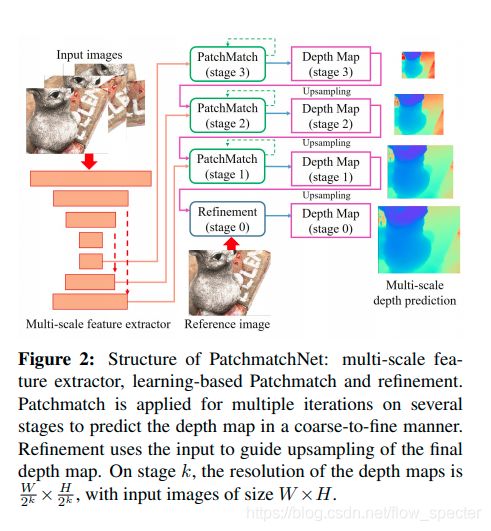
整体的结构中包括了几个大步骤，比如多尺度的特征提取，基于学习的patchmatch还有精化层。离不开的基础策略是从粗到精。

1 实践，跑个demo

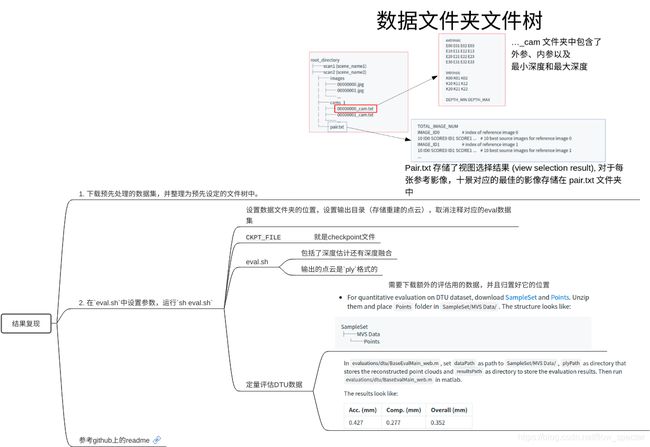
基于github主页上的readme信息，整理出了以下复现步骤，如导图中所示。

1.1 conda中新建环境

首先在anaconda中新建一个用于patchmatch测试学习的环境，我这里命名为patchmatchNetEnv。原先的环境中本来存在着一些冗余的环境，比如说aanetEnv环境，本想将其直接重命名为patchmatchNetEnv，但是conda中并不提供直接重命名的方法，因此，采取了克隆再删除的方式：

conda create -n patchmatchNetEnv --clone aanetEnv
conda remove -n aanetEnv --all

在这里多提一嘴关于requirements.txt的两点相关小知识。
不仅可以用pip安装，在conda环境里也可以用conda来安装，但是有时候会抛出来无包错误，此时就会希望转回用pip安装，那么能够实现这些希望的命令就是：
while read requirement; do conda install --yes $requirement || pip install $requirement; done < requirements.txt
------------------------------------------------------------------------------------------------
此外，还可以导出来一份以.yml为后缀的环境文件来给其他的人用，命令是：
conda env export > requirements.yml

这个时候，比如说其他人需要这个环境，那么直接可以用这个yml文件来创建出一个和你相同名字，相同库的环境，其他人需要运行的命令是：
conda env create -f requirements.yml

参考链接：https://blog.csdn.net/weixin_45092662/article/details/106906719

由于个人的硬件条件和作者的不一样，我查看了他的requirements.txt后，自己安装了相关的包。
我用的torch环境是：
conda install pytorch1.7.1 torchvision0.8.2 torchaudio==0.7.
2 cudatoolkit=11.0 -c pytorch

其他的自行安装即可，我这里运行的代码有：
pip install opencv-python等
。

1.2 下载数据，运行eval.sh，看看输出

下载数据就不讲了，直接根据github上给出的链接下载就是了。
观察eval.sh中的相关代码（单以DTU数据为例）：

# test on DTU's evaluation set
DTU_TESTING="/home/dtu/"
CKPT_FILE="./checkpoints/model_000007.ckpt"
python eval.py --dataset=dtu_yao_eval --batch_size=1 --n_views 5 \
--patchmatch_iteration 1 2 2 --patchmatch_range 6 4 2 \
--patchmatch_num_sample 8 8 16 --propagate_neighbors 0 8 16 --evaluate_neighbors 9 9 9 \
--patchmatch_interval_scale 0.005 0.0125 0.025 \
--testpath=$DTU_TESTING --geo_pixel_thres=1 --geo_depth_thres=0.01 --photo_thres 0.8 \
--outdir=./outputs --testlist lists/dtu/test.txt --loadckpt $CKPT_FILE $@

我下载的DTU数据放在了下图中的位置，对应修改了DTU_TESTING参数，然后在根据eval.sh新建了一个名为outdir的文件夹，用来接收输出的结果。

根据eval.sh中的命令测试dtu数据时，屏幕显示：

说明正在跑demo了。等到demo跑完，ouputs文件夹中出现了以下场面：

对于每个scanXX文件夹，长这个样子：

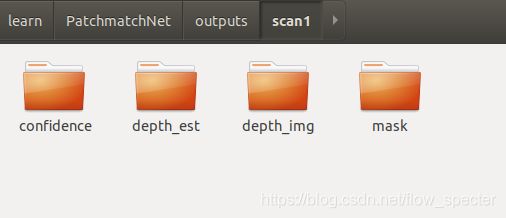
跑以上的demo的时候其实主要就是设置了一些环境变量，然后给eval.py文件传入了一些参数，非常简单。现在，我们希望能够深入地去找到核心源码，对应起来论文中的网络结构进行学习，那么，首先，我进一步地去查看了eval.py中都放了些什么。直接去看main函数里面做了什么，发现总共做了两件事，第一件：调用save_depth()函数，在其中使用模型保存了深度图还有置信图等进图片们到输出的文件夹，第二件：对已经保存的深度图进行基于几何约束的滤波，用的函数是filter_depth(…)。实际上，在eval.py中的函数有：

其中只有save_depth()函数调用了PatchmatchNet，而其他函数基本上都是一些辅助函数。因此，想要去结合demo，结合代码地去理解学习网络，我们就从save_depth()入手，直捣黄龙，进去patchmatchNet。patchmatchNet这个类存放于net.py文件夹中，在这个文件夹中，还有以下几个类和函数：

featureNet还有refinement都是在patchmatchNet中使用的。
其中，featureNet和refinement都在patchmatchnet的初始化中首现：

在利用patchmatchnet网络向前推断的时候就可以使用featurenet还是有refinement。现在，想要体会网络精髓，自然而然就要进到patchmatchNet的forward中进行学习，而这，也就是核心了。forward的代码学习和理论紧密结合，在2 理论中也会进行介绍。
纵览一遍patchmatchNet的forward函数，我挑出了几个python以及pytorch的知识点进行解读与学习，先使得我们没有语言上的障碍（就像英语阅读一样），为了尽可能保证阅读的连贯性，这些语言知识点放在了附录部分。

2 网络结构理论

在该章节中，将论文中的3 method部分及net.py中的patchmatNet类中的方法相对应地进行学习，尽可能做到逐句论文逐行代码的读懂消化吸收。

多尺度特征提取

论文中的描述

（注：这里是笔者个人的理解，并非逐字逐句的翻译，建议尽量去看原始论文，以下再说到论文中的描述时，将不再赘述）给定$N$张$W\ast H$大小的图像，参考图像命名为$I_0$，其他待匹配影像命名为$\{I_i{\}}_{i=1}^{N-1}$。需要从输入的影像中提取 逐像素的特征，类似于特征金字塔网络（Feature Pyramid Netword，简称FPN）。这些在不同分辨率下，分层地进行提取。如此，我们就可以得到不同分辨率下的，或者说不同尺度下的特征信息，这将有助于我们在不同尺度下进行深度估计，进而，施加从粗到精（coarse-to-fine）的策略。

代码中的描述

首先，看特征提取层在patchmatch网络中的逻辑：
对stage_0，也即原始分辨率中的影像，进行特征提取，取出参考影像的特征以及其他影像的特征，命名为ref_feature以及src_features。

深入到self.feature(img)中后，我们注意到：

1. 输入是经过torch.unbind的tensor元组。
2. 这无疑是一个初始化，那么给了featureNet什么样的初始化呢？我们可以进一步地，进到FeatureNet中去一探究竟。一点一点的挖掘出相关的知识信息。
   FeatureNet总共两个函数，一个初始化，一个forward。
   在初始化中：
   
   从conv0到conv10一共十一层的ConvBnReLU层，这个所谓的ConvBnReLU是自己定义的网络层，来源于module.py文件中，为：
   
   初始化的函数签名为：
   def __init__(self, in_channels, out_channels, kernel_size=3, stride=1, pad=1, dilation=1):
   输入的参数有输入的通道/维度in_channels，输出的通道/维度out_channels，卷积核的大小kernel_size，步长sride，补0的paddiing数值pad，以及kernel之间的间距dilation。这些参数都用来传递给nn.Conv2d以及nn.BatchNorm2d。ConvBnReLU层就是包装了卷积层，Bn层以及ReLU层。

基于学习的patchmatch

在这节里，由于代码比较多，逻辑相对比较细碎，和理论结合也紧密，所以先给出net.py中关于基于学习的patchmath的整体调用代码，然后再在后面的理论中，每讲到一个理论点的时候，就紧跟着关键代码。

net.py中的相关代码描述

这里先看net.py中的相关描述，逻辑我选择用注释来表示，主要描述了一层一层stage对patchmatch的调用。

# step 2. Learning-based patchmatch
        depth = None
        view_weights = None
        depth_patchmatch = {
     }
        refined_depth = {
     }
        
        # 时刻记得l是stage的层数，倒序开始的，比如说stage_3,stage_2,...然后stage_0这样
        for l in reversed(range(1, self.stages)):
            src_features_l = [src_fea[f'stage_{l}'] for src_fea in src_features]
            projs_l = getattr(self, f'proj_matrices_{l}')
            ref_proj, src_projs = projs_l[0], projs_l[1:]
            
            # 对于大于1层的stage，开始调用patchmatch了
            if l > 1:
                depth, _, view_weights = getattr(self, f'patchmatch_{l}')(ref_feature[f'stage_{l}'], 
                                        src_features_l, 
                                        ref_proj, src_projs, 
                                        depth_min, 
                                        depth_max, 
                                        depth=depth, 
                                        img=getattr(self,f'imgs_{l}_ref'), 
                                        view_weights=view_weights)
            else:
                depth, score, _ = getattr(self, f'patchmatch_{l}')(ref_feature[f'stage_{l}'], 
                                        src_features_l, 
                                        ref_proj, src_projs, 
                                        depth_min, 
                                        depth_max, 
                                        depth=depth,
                                        img=getattr(self,f'imgs_{l}_ref'), 
                                        view_weights=view_weights)
            
            del src_features_l, ref_proj, src_projs, projs_l

            depth_patchmatch[f'stage_{l}'] = depth
            # detach可以参考附录中的说明，这里取出了该stage的深度，之后就不能够对这个深度进行反向传播了
            depth = depth[-1].detach()
			# 如果层数大于1的话，要把这一层 的深度信息还有搜索影像之类的信息通过上采样的方式传递给下一个stage。
			# 这里，每一层都是两倍两倍的，所以内插的scale_factor是2
            if l > 1:
                # upsampling the depth map and pixel-wise view weight for next stage
                depth = F.interpolate(depth,
                                    scale_factor=2, mode='nearest')
                view_weights = F.interpolate(view_weights,
                                    scale_factor=2, mode='nearest')

上面只是一层一层stage的逻辑，重点还是要进到patchmatch去看，位置在patchmatch.py中。这个文件的outline是：

后边儿的理论基本上都在这个文件夹里体现了，当然了还有些在module.py中。

论文中的描述

3.2 Learning-based Patchmatch： 根据传统的Patchmatch方法，以及后续的深度估计的自适应相关工作 ^{1 2}。基于学习的patchmatch主要有三个步骤：

1. 初始化：生成一些随机的假设
   

2. 传播：将这些假设传播给周围的邻居们
   

3. 评估：对于所有的假设计算匹配代价，并且选择最好的解决方案
   

在初始化后，整个方法就在传播步骤以及评估步骤两个步骤之间反复横跳，直到迭代收敛。基于深度学习，可以提出一个传播模块的自适应版本以及评估模块的自适应版本，甚至，再整一个初始化的自适应版本。
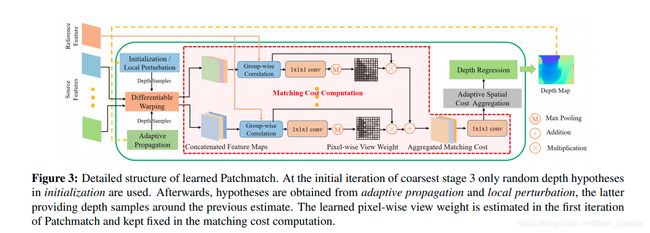
具体的基于学习的patchmatch的结构如下图所示：

总的来说，传播模块根据提取的特征自适应地，采样一些点去做传播，评估模块则自适应的为了代价计算而学着去对visibility的信息进行估计，并且自适应的采样周围的邻居们来聚合代价。限制于内存，并不像传统方法一样，把像素点们的假设形式化为倾斜的平面，取而代之的是，我们依靠学到的自适应评估来组织窗口内的空间模式，在该空间模式下计算匹配成本，其实就是自适应窗口，可形变卷积那种。

3.2.1 : Initialization and Local Perturbation
在初始的迭代时， 根据预设的深度范围$d_{min},d_{max}$，对每一个像素都随机地均匀地，扔给一个$D_f$，这个$D_f$是深度范围的倒数。对于在stage k层次上的后续迭代来说，对每个像素均匀地生成$N_k$个假设，当然了，这些假设的范围在归一化的深度范围倒数$R_k$之中，。对于更好的stage来说，这个深度范围也会逐渐地，慢慢地变小。为了能够定义$R_k$的中点在哪里，使用了前面迭代的估计，也就是从一个比较粗的stage上采样过来。这样做的好处是，对每个像素都给出了一个局部的扰动(local perturbation)。

class DepthInitialization(nn.Module):
    def __init__(self, patchmatch_num_sample = 1):
        super(DepthInitialization, self).__init__()
        self.patchmatch_num_sample = patchmatch_num_sample
		# 初始化的时候，要给出采样的数据的数目。
    
    def forward(self, random_initialization, min_depth, max_depth, height, width, depth_interval_scale, device, 
                depth=None):
        # 在使用初始化的时候，需要给出的信息是：是否是随机初始化？深度范围是？图片大小是？深度的间隔尺度是？用不用gpu？
        
        batch_size = min_depth.size()[0]
        # 如果是随机初始化，这个主要就针对stage3的第一次迭代：
        if random_initialization:
            # first iteration of Patchmatch on stage 3, sample in the inverse depth range
            # divide the range into several intervals and sample in each of them
            inverse_min_depth = 1.0 / min_depth
            inverse_max_depth = 1.0 / max_depth
            patchmatch_num_sample = 48 
            # [B,Ndepth,H,W]
            depth_sample = torch.rand((batch_size, patchmatch_num_sample, height, width), device=device) + \
                                torch.arange(0, patchmatch_num_sample, 1, device=device).view(1, patchmatch_num_sample, 1, 1)
       
            depth_sample = inverse_max_depth.view(batch_size,1,1,1) + depth_sample / patchmatch_num_sample * \
                                    (inverse_min_depth.view(batch_size,1,1,1) - inverse_max_depth.view(batch_size,1,1,1))
            
            depth_sample = 1.0 / depth_sample
           
            return depth_sample
        # 如果不是stage3的第一次迭代，或者说不用随机初始化的话，那就要再加上一些局部扰动了
        else:
            # other Patchmatch, local perturbation is performed based on previous result
            # uniform samples in an inversed depth range
            if self.patchmatch_num_sample == 1:
            	# 如果就采样一个数字，那就直接返回深度
                return depth.detach()
            else:
            	# 否则的话，就均匀的采样，再整点儿扰动吧
                inverse_min_depth = 1.0 / min_depth
                inverse_max_depth = 1.0 / max_depth
                
                depth_sample = torch.arange(-self.patchmatch_num_sample//2, self.patchmatch_num_sample//2, 1, 
                                    device=device).view(1, self.patchmatch_num_sample, 1, 1).repeat(batch_size,
                                    1, height, width).float()
                inverse_depth_interval = (inverse_min_depth - inverse_max_depth) * depth_interval_scale
                inverse_depth_interval = inverse_depth_interval.view(batch_size,1,1,1)
                
                depth_sample = 1.0 / depth.detach() + inverse_depth_interval * depth_sample
                
                depth_clamped = []
                del depth
                for k in range(batch_size):
                    depth_clamped.append(torch.clamp(depth_sample[k], min=inverse_max_depth[k], max=inverse_min_depth[k]).unsqueeze(0))
                
                depth_sample = 1.0 / torch.cat(depth_clamped,dim=0)
                del depth_clamped
                
                return depth_sample

3.2.2 : Adaptive Propagation

基于这样的假设：深度值的相关性通常存在于来自同一物理表面的像素，我们不是生硬地进行传播，而是自适应地尽可能在同一物理表面收集假设，这将相比无差别的收集更符合我们的认知。
这个自适应的传播，源于可形变卷积网络，说起来这个可变性网络在aanet里也用的挺好，可以理解为传统方法中的自适应窗口吧。为了得到在参考影像上像素$p$的$K_p$个深度假设，这个模型学习了额外的二维的偏移项$\{△o_i(p){\}}_{i=1}^{K_p}$，这个项什么意思，$i$的变化从1到$K_p$，也就是说对于每一个假设，都学习一个二维的偏移量，这些偏移量有什么用呢？将会应用到每个假设的常量的二维偏移量$\{o_i{\}}_{i=1}^{K_p}$之上（这里就没有$△$了，对于每一个深度假设有一个固定的值）。我们使用一个2D CNN 层在参考影像的特征图$F_0$的后边，来学习每个像素的额外的2D偏移量。此外，通过双线性内插来得到那些深度的假设值们$D_p(p)$：

$$D_p(\text{p})=\{\text{D}(\text{p}+{\text{o}}_i+△{\text{o}}_i(\text{p})){\}}_{i=1}^{K_p}$$

3.2.3 : Adaptive Evaluation

自适应的评估模块有以下的步骤：

1. 可微分的warping (differentiable warping)
2. 匹配代价计算
3. 自适应的空间代价传播以及深度回归
   评估模块对于每一个stage都是一样的，在数学表达的时候就不单独给出脚标了。

Differentiable Warping
已知内参矩阵是$\{K_i{\}}_{i=0}^K$，以及参考影像（编号为0）以及搜索影像（编号为i）之间的变换矩阵
$\{[R_{0,i}|t_{0,i}]{\}}_{i=1}^K$，现在对于参考影像中的某个像素$p$，将其在其他搜索影像中的对应候选的像素点$p_{i,j}$定义为$p_i{d}_j$，定义深度假设$d_j$为$d_j(p)$，那么可以通过这些信息，找到参考影像中的$p$点在其他影像中的对应点为：

$$p_{i,j}=K_i\cdot (R_{0,i}\cdot （K_0^{-1}\cdot p\cdot d_j）+t_{0,i})$$

代码体现为module.py中的differentiable_warping函数。

def differentiable_warping(src_fea, src_proj, ref_proj, depth_samples):
    # src_fea: [B, C, H, W]
    # src_proj: [B, 4, 4]
    # ref_proj: [B, 4, 4]
    # depth_samples: [B, Ndepth, H, W] 
    # out: [B, C, Ndepth, H, W]
    batch, channels, height, width = src_fea.shape
    num_depth = depth_samples.shape[1]
    
    with torch.no_grad():
        proj = torch.matmul(src_proj, torch.inverse(ref_proj))
        rot = proj[:, :3, :3]  # [B,3,3]
        trans = proj[:, :3, 3:4]  # [B,3,1]

        y, x = torch.meshgrid([torch.arange(0, height, dtype=torch.float32, device=src_fea.device),
                            torch.arange(0, width, dtype=torch.float32, device=src_fea.device)])
        y, x = y.contiguous(), x.contiguous()
        y, x = y.view(height * width), x.view(height * width)
        xyz = torch.stack((x, y, torch.ones_like(x)))  # [3, H*W]
        xyz = torch.unsqueeze(xyz, 0).repeat(batch, 1, 1)  # [B, 3, H*W]
        rot_xyz = torch.matmul(rot, xyz)  # [B, 3, H*W]

        rot_depth_xyz = rot_xyz.unsqueeze(2).repeat(1, 1, num_depth, 1) * depth_samples.view(batch, 1, num_depth,
                                                                                            height * width)  # [B, 3, Ndepth, H*W]
        proj_xyz = rot_depth_xyz + trans.view(batch, 3, 1, 1)  # [B, 3, Ndepth, H*W]
        # avoid negative depth
        negative_depth_mask = proj_xyz[:, 2:] <= 1e-3
        proj_xyz[:, 0:1][negative_depth_mask] = width
        proj_xyz[:, 1:2][negative_depth_mask] = height
        proj_xyz[:, 2:3][negative_depth_mask] = 1
        proj_xy = proj_xyz[:, :2, :, :] / proj_xyz[:, 2:3, :, :]  # [B, 2, Ndepth, H*W]
        proj_x_normalized = proj_xy[:, 0, :, :] / ((width - 1) / 2) - 1 # [B, Ndepth, H*W]
        proj_y_normalized = proj_xy[:, 1, :, :] / ((height - 1) / 2) - 1
        proj_xy = torch.stack((proj_x_normalized, proj_y_normalized), dim=3)  # [B, Ndepth, H*W, 2]
        grid = proj_xy      

    warped_src_fea = F.grid_sample(src_fea, grid.view(batch, num_depth * height, width, 2), mode='bilinear',
                                padding_mode='zeros',align_corners=True)
    
    warped_src_fea = warped_src_fea.view(batch, channels, num_depth, height, width)

    return warped_src_fea

Matching Cost Computation
对于MVS问题来说，在计算代价的时候，必须要综合任意多个搜索影像的信息到一个视差空间的格网中。为此，代价的计算假设通过group-wise的相关进行³，而在这些影像之间的聚合则通过加权来进行^{4 5 6} (为什么可以group-wise，怎么个group_wise法？见附录)。之后，group-wise的代价再通过一个小小的网络投影到一个单独的数字以及视差空间中的格网。
让${\mathbf{F}}_0(\mathbf{p})$，${\mathbf{F}}_i({\mathbf{p}}_{i,j})\in {\mathbb{R}}^C$ 代表参考影像以及搜索影像的特征图的一纵溜儿，注意了，时刻记得i代表的是影像的续标，而p是一个像素，这儿都写了这两的特征就一个维度，长度是$C$，那现在就可以没有什么歧义地将特征图的通道平均的分成G个group。第g个群体的相似度${\mathbf{S}}_i(\mathbf{p},j{)}^g\in \mathbb{R}$的计算方式是：
$${\mathbf{S}}_i(\mathbf{p},j{)}^g=\frac{G}{C}⟨{\mathbf{F}}_0(\mathbf{p}{)}^g,{\mathbf{F}}_i({\mathbf{p}}_i,j{)}^g⟩$$
使用${\mathbf{S}}_i(\mathbf{p},j)\in {\mathbb{R}}^G$来标注各个group的相似性向量。在假设以及像素上的聚集使得${\mathbf{S}}_i\in {\mathbf{R}}^{W\ast H\ast D\ast G}$。为了找到对应每一个像素的相应视图们的权重，表达为$\{\mathbf{w}(\mathbf{p}){\}}_{i=1}^{N-1}$，那么很自然的，我们可以用${\mathbf{w}}_i(\mathbf{p})$来代表像素$p$在搜索影像${\mathbf{I}}_i$上的灰度信息（其实原文是visibility information, 我的理解应该是包括彩色信息之类的，但是我更喜欢说成灰度信息）。这些权重仅仅计算一次，然后就固定住，通过上采样将其传递给更精细的satge。一个简单的逐像素的权重网络，包括了3D的卷积层（卷积核的大小为111）以及非线性的sigmoid函数，这个网络的输入是初始的相似性测度${\mathbf{S}}_i$，输出是一个0到1的数值，这个输出是针对每一个视差格网的，进而，给出${\mathbf{P}}_i\in {\mathbb{R}}^{W\ast H\ast D}$，时刻记得$i$是搜索影像的序标，而$W\ast H\ast D$就让人脑子里浮现出了视差空间，所以说对于每一个影像，都有一个三维的视差空间，也就是说，对于每一个像素的候选视差（也就是每一个视差空间的格网）来说，都能够拿到搜索影像$I_i$ 的权重信息，但是，我们真的想要对每个视差都要整一个权重吗？不是的，我们只想要针对这个平面像素的一个，就一个对应搜索影像$I_i$的权重就可以了，怎么从一个集里拿到一个数值呢？这里用max的方法：
$${\mathbf{w}}_i(\mathbf{p})=\max \{{\mathbf{P}}_i(\mathbf{p},j)|j=0,1,...,D-1\}$$
现在，已知了每个搜索影像的权重，就可以对视差空间的三维格网加权平均地进行赋值：
$$\overline{\mathbf{S}}(\mathbf{p},j)=\frac{{\sum }_{i=1}^{N-1}{\mathbf{w}}_i(\mathbf{p})\cdot {\mathbf{S}}_i(\mathbf{p},j)}{{\sum }_{i=1}^{N-1}{\mathbf{w}}_i(\mathbf{p})}$$

接着，我们希望为每一个视差空间的三维格网都构建一个$\overline{\mathbf{S}}(\mathbf{p},j)$，但是这是对应一个group的，也就是说，$\overline{\mathbf{S}}$的维度是四维的，即，$W\ast H\ast D\ast G$，想要使用这些个$\overline{\mathbf{S}}(\mathbf{p},j)$来构建出一个完整的代价空间，还需要使用一个核为$1\times 1\times 1$的3D卷积进行降维。

对应代码包括patchmatch.py中的SimilarityNet类。

# first, do convolution on aggregated cost among all the source views
# second, perform adaptive spatial cost aggregation to get final cost

class SimilarityNet(nn.Module):
    def __init__(self, G, neighbors = 9):
        super(SimilarityNet, self).__init__()
        self.neighbors = neighbors
        
        self.conv0 = ConvBnReLU3D(G, 16, 1, 1, 0)
        self.conv1 = ConvBnReLU3D(16, 8, 1, 1, 0)
        self.similarity = nn.Conv3d(8, 1, kernel_size=1, stride=1, padding=0)
        
    def forward(self, x1, grid, weight):
        # x1: [B, G, Ndepth, H, W], aggregated cost among all the source views with pixel-wise view weight
        # grid: position of sampling points in adaptive spatial cost aggregation
        # weight: weight of sampling points in adaptive spatial cost aggregation, combination of 
        # feature weight and depth weight
        
        batch,G,num_depth,height,width = x1.size() 
        
        x1 = self.similarity(self.conv1(self.conv0(x1))).squeeze(1)
        
        x1 = F.grid_sample(x1, 
                        grid, 
                        mode='bilinear',
                        padding_mode='border')
        
        # [B,Ndepth,9,H,W]
        x1 = x1.view(batch, num_depth, self.neighbors, height, width)
    
        return torch.sum(x1*weight, dim=2)
        

其中，ConvBnReLU3D类在module.py中出现:

class ConvBnReLU3D(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size=3, stride=1, pad=1, dilation=1):
        super(ConvBnReLU3D, self).__init__()
        self.conv = nn.Conv3d(in_channels, out_channels, kernel_size, stride=stride, padding=pad, dilation=dilation, bias=False)
        self.bn = nn.BatchNorm3d(out_channels)

    def forward(self, x):
        return F.relu(self.bn(self.conv(x)), inplace=True)

Adaptive Spatial Cost Aggregation
多尺度的特征提取其实已经做了一部分的聚集工作了。为了避免聚集那些边缘的像素点，采取了自适应的空间代价聚集方式。对于每一个包含$K_e$个像素的窗口${\left\{{\mathbf{p}}_k\right\}}_{k=1}^{K_e}$，我们学习每个像素额外的偏移量${\left\{\Delta {\mathbf{p}}_k\right\}}_{k=1}^{K_e}$。
然后，聚集的空间代价就可以表示为：
$$\tilde{\mathbf{C}}(\mathbf{p},j)=\frac{1}{{\sum }_{k=1}^{K_e}{w}_k{d}_k}\sum _{k=1}^{K_e}{w}_k{d}_k\mathbf{C}\left(\mathbf{p}+{\mathbf{p}}_k+\Delta {\mathbf{p}}_k,j\right)$$
对于特征比较贫瘠的区域，窗口将会更大一些，尽可能的包含更多的有效信息进来。
以patchmatch.py中的get_evaluation_grid函数为例：

    # compute the offests for adaptive spatial cost aggregation in adaptive evaluation
    def get_evaluation_grid(self, batch, height, width, offset, device, img=None):
        
        if self.evaluate_neighbors==9:
            dilation = self.dilation-1 #dilation of evaluation is a little smaller than propagation
            original_offset = [[-dilation, -dilation], [-dilation, 0], [-dilation, dilation],
                                [0,             -dilation], [0,              0], [0,              dilation],
                                [dilation, -dilation], [dilation,  0], [dilation,  dilation]]
        elif self.evaluate_neighbors==17:
            dilation = self.dilation-1
            original_offset = [[-dilation, -dilation], [-dilation, 0], [-dilation, dilation],
                                [0,             -dilation], [0,              0], [0,              dilation],
                                [dilation, -dilation], [dilation,  0], [dilation,  dilation]]
            for i in range(len(original_offset)):
                offset_x, offset_y = original_offset[i]
                if offset_x != 0 or offset_y !=0:
                    original_offset.append([2*offset_x, 2*offset_y])
        else:
            raise NotImplementedError
        
        with torch.no_grad():
            y_grid, x_grid = torch.meshgrid([torch.arange(0, height, dtype=torch.float32, device=device),
                                torch.arange(0, width, dtype=torch.float32, device=device)])
            y_grid, x_grid = y_grid.contiguous(), x_grid.contiguous()
            y_grid, x_grid = y_grid.view(height * width), x_grid.view(height * width)
            xy = torch.stack((x_grid, y_grid))  # [2, H*W]
            xy = torch.unsqueeze(xy, 0).repeat(batch, 1, 1)  # [B, 2, H*W]

        xy_list=[]
        for i in range(len(original_offset)):
            original_offset_y, original_offset_x = original_offset[i]
            
            offset_x = original_offset_x + offset[:,2*i,:].unsqueeze(1)
            offset_y = original_offset_y + offset[:,2*i+1,:].unsqueeze(1)
            
            xy_list.append((xy+torch.cat((offset_x, offset_y), dim=1)).unsqueeze(2))
            
            
        xy = torch.cat(xy_list, dim=2)    # [B, 2, 9, H*W]
        
        del xy_list, x_grid, y_grid
        x_normalized = xy[:, 0, :, :] / ((width - 1) / 2) - 1
        y_normalized = xy[:, 1, :, :] / ((height - 1) / 2) - 1
        del xy
        grid = torch.stack((x_normalized, y_normalized), dim=3)  # [B, 9, H*W, 2]
        del x_normalized, y_normalized
        grid = grid.view(batch, len(original_offset) * height, width, 2)
        return grid

Depth Regression
将代价空间转变为概率$\mathbf{P}$，得到子像素的回归深度值以及置信度。具体来说，回归的深度值$\mathbf{D}(\mathbf{p})$计算表达为：
$$\mathbf{D}(\mathbf{p})=\sum _{j=0}^{D-1}{d}_j\cdot \mathbf{P}(\mathbf{p},j)$$

深度图的Refinement层

论文描述

对应文章3.3。
在refinement层里，参考了MSG-Net，设计了一个深度残差网络（depth residual network）。为了避免尺度的偏移之类的问题，预先将输入的深度图数值归至0到1之间，然后refinement完了之后再给他们转变回来。这一层输出的是残差，这个残差将对加到由Patchmatch所估计得到的$\mathbf{D}$上，来得到一个精化后的${\mathbf{D}}_{ref}$。这个网络独立的从patchmatch输出的视差结果图以及参考影像 $I_0$中分别提取特征图${\mathbf{F}}_D$以及${\mathbf{F}}_I$，并且对${\mathbf{F}}_D$应用解卷积操作来达到上采样的目的，上采样到什么程度呢?到达影像大小的程度。为了得到这个残差，refinement层里其实包括了许多个2D卷积层，施加到刚才说的独立提取的特征图中。

关键代码描述

在net.py中的相关表达：

进到upsample_net,即Refinement类中：

损失函数

对应文章中的3.4。
这个损失函数涉及的对象是在估计的深度与渲染过的地面真值，损失函数具体表达为：
$$L_{\text{total }}=\sum _{k=1}^3\sum _{i=1}^{n_k}{L}_i^k+L_{\text{ref }}^0$$
其中，对于每一个stage k的每一个迭代 i的损失$L_i^k$来说，采用的都是$L1$损失，而$L_{ref}^0$则是最后的那个被refine过的深度层的$L1$损失。

附录

Latex写作小技巧

$△$ ： \triangle
显示直立文本： \textup{文本} $\text{文本D}$
意大利斜体： \textit{文本} $\text{文本D}$
显示小体大写文本： 　\textsc{文本}
中等权重： \textmd{文本}
加粗命令： \textbf{文本} $\text{文本D}$
默认值： \textnormal{文本}
点 $\cdot$ \cdot
公式： $$ 回车 $$
行内公式 $$
空心R $\mathbb{R}$： \mathbb {R}
希博尔特内积 $⟨x,y⟩$ ： \left< x,y \right>
加^号 输入\hat 或 \widehat
加横线 输入 \overline
加波浪线 输入 \widetilde
加一个点 \dot{要加点的字母}加两个点\ddot{要加点的字母}

---

相关英文表达学习

---

local perturbation: 局部摄动
refrain: 避免
------例句：“UnLike[3, 16, 38], we refrain from parameterizing the per-pixel hypothesis as a slanted plane, due to heavy memory penalties.”

MVS代价计算中的group-wise

（待写）

为什么内积可以表示相似度？

和内积相关的是余弦相似度来衡量相似性的，只是取点积的化，可以通过让向量变大的方式来作弊,那么为什么要这样做呢
1、点积是最简单的操作，如果余弦相似需要更多的数学运算，增加计算复杂度
因此可以用点积的大小表示相似度的大小。
参考链接

deconvolution

试图从特征变换回影像信息

smooth L1损失

${\mathrm{smooth}}_{L_1}(x)=\{\begin{array}{ll}0.5x^2& \text{ if }|x|<1\\ |x|-0.5& others\end{array}$
能够解决L1离群点梯度爆炸的问题
参考链接

torch.unbind(input, dim=0) → seq

作用是返回tensor维度切片后的元组。比如说，X是一个这样的tensor：

经过了torch.unbind(x, 1)后，就变成了一纵溜儿一纵溜儿的这样：

既然说到了返回的是元组，那再复习一下Python的元组的相关知识：
元组不可修改，用的是括号； 访问用的是切片； 元组理论上是不可以修改的，但是可以连接组合； 理论上是不可以删除的，但是可以通过del语句删除整个元组； 常用的运算符有加号和乘号； 任何没有符号的对象，用逗号隔开的，默认都是元组； 元组内置的函数有cmp、len、max、min、tuple等，作用分别为比较元组元素、计算元组个数、返回最大值最小值以及将列表转换为元组。 参考链接：https://www.runoob.com/python/python-tuples.html
参考链接：https://blog.csdn.net/DreamHome_S/article/details/106032025

reversed函数

在代码中出现的地方：

reversed(seq)函数是python内置的函数，返回的是一个反转的迭代器，输入的参数是需要转换的序列，可以是tuple，string，list或者range。既然在代码里是range，那么举一个range的例子：

输出是：

参考链接：https://www.runoob.com/python3/python3-func-reversed.html

getattr(obj, key, def)函数

参考链接：https://www.geeksforgeeks.org/python-getattr-method/

F.avg_pool3d

代码中出现的位置：

官方文档中的相关信息：

其实就是对三维格网做平均池化操作。

torch.clamp()

clamp参考链接

torch.gather

• 代码中出现的位置：
  
• 官方文档：
  

torch.meshgrid

功能： 生成网格，或者生成坐标。应用有比如将图像划分成网格。
举例：
参考链接

colmap以及meshlab的安装

为了去查看.ply文件，我另外去安装了colmap还有meshlab（反正之后都是要用的），colmap的安装直接参考官网链接https://colmap.github.io/install.html，讲的非常清楚。但是在编译安装的过程中笔者遇到了两次报错，一次是在cmkae … 命令时，关于libGL.so的报错，我重新建立软连接后好了，再报错是在make的时候，见下图：
解决方法是在cmakelists中加一句：
SET(CMAKE_PREFIX_PATH "/usr/lib/x86_64-linux-gnu/cmake")
解决方法所参考的链接是：https://blog.csdn.net/qq_19707521/article/details/108730920
colmap安装好并运行colmap gui后长这样：

meshlab的安装：参考的链接是https://blog.csdn.net/m0_45388819/article/details/109867622。安装后，根据它提供的1_build.sh，发现安装路径不是系统的路径，所以直接运行meshlab没什么反应，因为meshlab的可执行程序在这个位置：

运行meshlab，并且随便拖进去一个outputs文件夹中的.ply文件后，长这样：
**
**

nn.Conv2d、nn.BatchNorm2d、F.Relu知识点

• 先来看nn.Conv2d，整体的函数为Torch.nn.Conv2d(in_channels，out_channels，kernel_size，stride=1，padding=0，dilation=1，groups=1，bias=True),其中前面的参数就不赘述了，直接结合上面的ConvBnReLU的参数输入进行理解吧，这里说一下bias参数，bias是bool类型的，如果将其设置为false，那么对于卷积操作$f(x)=wx+b$来说，就扔掉了b项，这对于某些时候是有道理的，比如说下一层是Bn层的时候，就没必要留着b(参考链接)。此外，再记录一下输入维度和输出维度之间的关系：
  
  nn.Conv2d参考链接
• 其次来看nn.BatchNorm2d。
  首先在理论层面讲一下BatchNorm2d的意义，通常来说，BatchNorm2d经常出现在卷积层的后面，在这里的ConvBnReLU就可以看出来了，其作用是对数据进行归一化处理，以期数据在进行ReLU前不会因为数据变化太大，导致网络不稳定。ConvBnReLU整体的顺序也是先卷积，然后Bn，再然后ReLU。其实这个层就是为了方便做这一套操作。
  
  
  BatchNorm2d的输入输出不改变维度。参考链接：
  https://pytorch.org/docs/stable/generated/torch.nn.BatchNorm2d.html
• 最后来看F.Relu。其实nn也有relu那么nn.relu()和F.relu()有什么区别呢？其实这跟个人的编程风格有关，nn.relu()将创建网络结构中的一层，而F.relu()则更像一个功能性的API，只是做了relu()的工作，通常来说，在forward方法中，用F.relu()多一些。F.relu()与nn.relu()区别的
  参考链接
  下图为F.relu的官方介绍

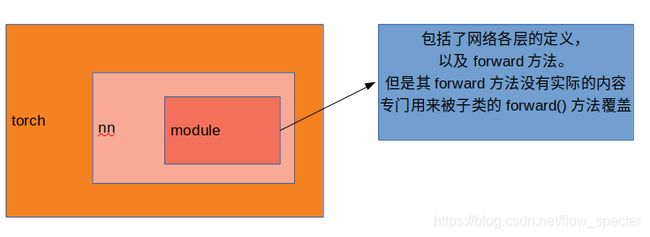
nn.module知识点

首先，所有的网络都要继承nn.module，torch.nn是专门为了神经网络所设计的接口，nn.module则是nn中非常重要的类，里面包含了网络各层的定义，还有forward方法。

forward方法在nn.module中的__call__方法被调用:

又或者说module中存有内置的__call__函数，可以直接将实例当成函数调用，所以在代码中才会有output_feature = self.feature(img)，这句其实直接就调用了featureNet的forward函数了。

再往下看，注意到，FeatureNet在__init__()中，除去
11个ConvBnReLU层以外，还有三个output层以及两个inner层，如下图所示：

可见，三个的output层应对应不同stage的输出，或者说，对应不同分辨率的特征提取输出。
看完featureNet的__init__函数后，再去看其的forward实现。
首先是从0层到10层的ConvBnReLU层层卷积，然后前面十一层的卷积结果送进output1也就是再送一层Conv2d作为stage3的特征输出，注意到output1的输出维度是64，这层的特征输出的是最大块儿的，也就自然对应着分辨率比较粗的stage_3。
后面stage_2还有stage_1的特征则通过以下代码进行获取：

F.interpolate()

主要用以上采样、下采样的等工作。通过插值的方式变化size。

举例（参考链接）：

参考文献

---

1. Michael Bleyer, Christoph Rhemann, and Carsten Rother.Patchmatch stereo - stereo matching with slanted supportwindows. InBritish Machine Vision Conference (BMVC),2011. ↩︎

2. Silvano Galliani, Katrin Lasinger, and Konrad Schindler.Massively parallel multiview stereopsis by surface normaldiffusion. InInternational Conference on Computer Vision(ICCV), 2015. ↩︎

3. Qingshan Xu and Wenbing Tao. Learning inverse depth regression for multi-view stereo with correlation cost volume.InAAAI, 2020. ↩︎

4. Johannes Lutz Sch ̈onberger and Jan-Michael Frahm.Structure-from-Motion Revisited. InConference on Com-puter Vision and Pattern Recognition (CVPR), 2016 ↩︎

5. Qingshan Xu and Wenbing Tao. Multi-scale geometric con-sistency guided multi-view stereo. InConference on Computer Vision and Pattern Recognition (CVPR), 2019. ↩︎

6. Qingshan Xu and Wenbing Tao.PVSNet:Pixelwise visibility-aware multi-view stereo network.ArXiv, 2020. ↩︎