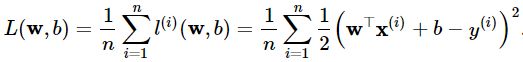动手学深度学习-线性回归；Softmax与分类模型；多层感知机

 

前言

由于新冠病毒的影响，只能窝在家中自我关禁闭，因此参加了深度学习公益训练营的活动，结合《动手学深度学习》这本书，对深度学习进行系统性的学习与实践，感到获益良多。

一、线性回归

回归问题通常对连续值进行预测，而分类问题通常对离散的值进行预测。线性回归输出是⼀个连续值，因此适⽤于回归问题。回归问题在实际中很常⻅，如预测房屋价格、⽓温、销售额等连续值的问题；分类问题包括图像分类、垃圾邮件识别、疾病检测等输出为离散值的问题。

模型

这里以房价预测为例，假设价格只取决于房屋状况的两个因素，即面积（平方米）和房龄（年）。线性回归假设输出与各个输入之间是线性关系，考虑通过房屋的面积Area与房龄Age来预测房价Price，其中w和b为未知的模型参数，即需要学习的参数。

数据集

我们通常收集一系列的真实数据作为数据集，例如多栋房屋的真实售出价格和它们对应的面积和房龄。目标是在这个数据的基础上训练模型参数使模型的预测价格与真实价格的误差最小。其中数据集被称为训练数据集（training data set）或训练集（training set），一栋房屋被称为一个样本（sample），其真实售出价格叫作标签（label），用来预测标签的两个因素叫作特征（feature）。特征用来表征样本的特点。

损失函数

在模型训练中，我们需要衡量价格预测值与真实值之间的误差。通常我们会选取一个非负函数作为误差，其数值越小表示误差越小。一个常用的函数就是均方误差。 单个样本误差的表达式为：

小批量样本的误差表达式为：

优化算法

通过优化函数有限次迭代模型参数尽可能降低误差函数的值，优化函数有两个步骤：

• (i)初始化模型参数，一般来说使用随机初始化；
• (ii)我们在数据上迭代多次，通过在负梯度方向移动参数来更新每个参数。

本例采用随机梯度下降算法。

在求数值解的优化算法中，小批量随机梯度下降（mini-batch stochastic gradient descent）在深度学习中被广泛使用。它的算法很简单：先选取一组模型参数的初始值，如随机选取；接下来对参数进行多次迭代，使每次迭代都可能降低损失函数的值。在每次迭代中，先随机均匀采样一个由固定数目训练数据样本所组成的小批量（mini-batch）B，然后求小批量中数据样本的平均损失有关模型参数的导数（梯度），最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。

二、Softmax与分类模型

分类问题

softmax用于解决分类问题，例如一个简单的图像分类问题，输入图像的高和宽均为2像素，色彩为灰度。图像中的4像素分别记为x1,x2,x3,x4。假设真实标签为狗、猫或者鸡，这些标签对应的离散值为y1,y2,y3。通常使用离散的数值来表示类别，例如y1=1,y2=2,y3=3。

权重矢量

与回归问题不同的是，输出个数等于标签类别数，权重矢量为：

神经网络图

下图用神经网络图描绘了上面的计算。softmax回归同线性回归一样，也是一个单层神经网络。由于每个输出o1,o2,o3o1,o2,o3的计算都要依赖于所有的输入x1,x2,x3,x4x1,x2,x3,x4，softmax回归的输出层也是一个全连接层。

两个问题

1. 输出层的输出值的范围不确定，我们难以直观上判断这些值的意义。
2. 真实标签是离散值，这些离散值与不确定范围的输出值之间的误差难以衡量。

为了解决这两个问题，采用softmax运算符将输出值变换成值为正且和为1的概率分布：

这样softmax运算符不会改变输出类别。

计算效率

为了提高计算效率，我们可以将单样本分类通过矢量计算来表达。在上面的图像分类问题中，假设softmax回归的权重和偏差参数分别为：

交叉熵损失函数

分类问题并不需要预测概率完全等于标签概率，因此均方误差函数过于严格，因此需要采用更适合衡量两个概率分布差异的测量函数，交叉熵（cross entropy）是一个常用的衡量方法：

模型训练与预测

在训练好softmax回归模型后，给定任一样本特征，就可以预测每个输出类别的概率。通常，我们把预测概率最大的类别作为输出类别。如果它与真实类别（标签）一致，说明这次预测是正确的。

三、多层感知机

深度学习主要关注多层模型。以多层感知机（multilayer perceptron，MLP）为例，介绍多层神经网络的概念。

隐藏层

会发现不论隐藏层设置多少层，均等价于单层的神经网络输出：

激活函数

解决上述问题的一个方法是引入非线性变换，例如对隐藏变量使用按元素运算的非线性函数进行变换，然后再作为下一个全连接层的输入。这个非线性函数被称为激活函数（activation function）。下面介绍几种常用的激活函数：

ReLU函数

ReLU（rectified linear unit）函数提供了一个很简单的非线性变换。给定元素xx，该函数定义为

Sigmoid函数

sigmoid函数可以将元素的值变换到0和1之间：

tanh函数

tanh（双曲正切）函数可以将元素的值变换到-1和1之间：

激活函数的选择

ReLu函数是一个通用的激活函数，目前在大多数情况下使用。但是，ReLU函数只能在隐藏层中使用。

用于分类器时，sigmoid函数及其组合通常效果更好。由于梯度消失问题，有时要避免使用sigmoid和tanh函数。

在神经网络层数较多的时候，最好使用ReLu函数，ReLu函数比较简单计算量少，而sigmoid和tanh函数计算量大很多。

在选择激活函数的时候可以先选用ReLu函数如果效果不理想可以尝试其他激活函数。

多层感知机

多层感知机是含有至少一个隐藏层的由全连接层组成的神经网络，且每个隐藏层的输出通过激活函数进行变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。以单隐藏层为例并沿用本节之前定义的符号，多层感知机按以下方式计算输出：