祖思机——第一台二进制可编程计算机
巴贝奇领先全人类一个世纪提出了可编程机械计算机的设想,但最终没能将其转换为现实——分析机的建造甚至迄今都没有人能完成。历史翘首期盼了百年,却在纳粹德国见证了第一台可编程计算机的诞生。
它的发明者——康拉德·祖思(Konrad Zuse)虽不为人所熟知,却是名副其实的“现代计算机之父”。
祖思出生于柏林,从小聪慧过人,长大后进入世界顶尖学府——柏林工业大学学习工程学和建筑学,不久后又转读土木工程。1935年毕业后,在福特汽车公司工作不久后跳槽至另一家交通行业的巨头——亨舍尔。亨舍尔公司从1933年开始建造军用飞机,祖思负责飞机在飞行过程中的受力分析,要解各种各样的微分方程。这份在外人眼中的高智商工作,在祖思看来却无异于体力劳动,他被大量的重复运算损耗着精力,无暇顾及更有价值的创造性设计。尽管办公桌上配有一台当时先进的手摇计算器,但他仍然觉得很不方便。
1936年,祖思便辞职回家,决定建造一台更便捷的计算机器。他的父母十分开明,把整个客厅腾出来作为他的工作室。
Z1
1938年,第一台祖思机——Z1建造完成。这是一台纯机械的机器,由成千上万的金属片和金属杆组成,靠电动马达驱动运转。Z1从未投入实际使用,并连同图纸毁于1944年1月30日的一场空袭。
1987~1989年,在西门子公司的资助下,祖思在欣费尔德的家中重建了Z1。移交柏林德国技术博物馆时,为了顺利起吊这组重达1吨的精密钢铁,祖思家里的墙面都被拆除了一部分。下图为德国技术博物馆展厅中的Z1,后人对Z1的了解基本源自这台复制品。
工作原理
与以往靠齿轮实现计算的机械设备大不相同,Z1是二进制的。从机身侧视,可以看到下层一列列整齐的金属杆支撑着上层一叠叠整齐的金属片,像极了建筑工地上正在打地基的楼房胚子。
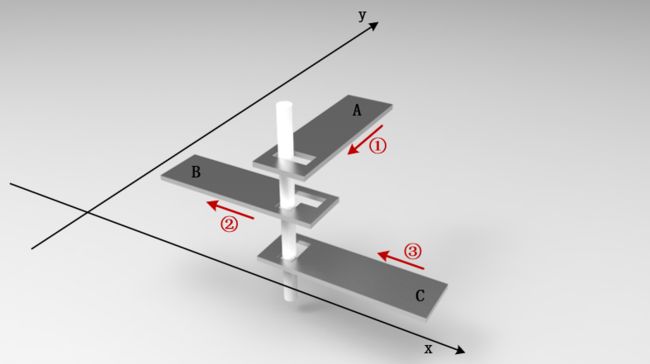
它们是如何相互作用完成二进制计算的呢?靠的是金属片和金属杆在水平面内4个方向(前后左右)的移动。下面给出了一组基础零件的作用关系,为便于说明,附加了直角坐标系,所有平移可描述为沿x轴或y轴正负方向的移动。金属杆穿过金属片A、B、C上的孔洞,将4者的平移关联起来,其中A和B在马达的动力下主动平移,进而带动C和金属杆的平移。
A可沿y轴正负方向平移,正向平移之后的状态表示0(如图(a)所示),负向平移之后的状态表示1(如图(b)所示)。A在自身移动的同时会带动金属杆也沿着y轴平移,B上的孔洞是L形的,金属杆在A的带动下,在B上y轴方向的孔洞段内移动。
- 图(a)中,A处于位置0,金属杆位于B孔洞的折角处,此时B沿x轴负方向移动,将无法带动金属杆,C不发生位移;
- 图(b)中,A处于位置1,金属杆位于B孔洞的顶端,此时B沿x轴负方向移动,将带动金属杆也沿x轴负方向移动,随之,C在金属杆的带动着也沿x轴方向移动。
通过这一过程,A将便将自己的二进制状态传递给了C。基于这一基本结构,祖思成功地实现了机械式的逻辑门。
组成结构及二进制存储原理
Z1在组成上已初具现代计算机的特点,主要包括控制器、存储器、运算器、输入设备(穿孔带读取器和十进制输入面板)和输出设备(十进制输出面板)5大部分。
和制表机一样,Z1也用到了穿孔技术,不过不是穿孔卡片,而是穿孔带,由废旧的35毫米电影胶卷制成。
穿孔带上只存储指令,数据通过输入面板置入。穿孔带上一行有8个孔位,即指令编码长8位,前2位表示存储器读写指令,后6位表示存储地址,或者仅用前3位表示四则运算和数据输入输出指令。因此,共支持读存储器、写入存储器、加法运算、减法运算、乘法运算、除法运算、数据输入和数据输出8种指令。
由于使用6位表示存储地址,因此Z1的存储器一共可以存放26(即64)条数据,用计算机的专业术语讲,就是存储容量为64字(此处介绍的是Z1复制品,原Z1的存储容量为16字)。那么,每条数据是如何以二进制的形式存储的呢?
我们先从十进制切入。
在Z1之前,本书所介绍的大部分计算工具或设备都采用了十进制来表示数据,且通常在原理上只考虑了整数的运算,在计算小数时,需要人为地确定小数点的位置。部分机器提供了临时标识小数点的滑块或按键(如奥德纳的销轮计算器、菲尔特的按键式计算器等),也仅是方便使用者辨认而已。比如要用某台支持6位数的设备计算加法1024+20.48,使用者需将小数点定在从左至右第4个数位后面,置数时分别置入102400和002048:
可以说,小数点的本质作用是对两个不同精度的数进行对其和前后补零。
这种在计算前定好小数点位置的做法,在计算机术语中被称为数据的定点数(fixed-point number)表示法。这种做法的好处就是实现简单,但也明显限制了可表示的数据范围,比如上面这台6位数的机器就连1024+2.048都计算不了。
于是就有了浮点数(floating-point number)表示法。
我们知道,任何一个实数都可以用科学记数法写成a×10n的形式。1024可以写成1024×101,也可以写成1.024×103。为了对齐小数点,我们规定所有数据都写成后一种形式(小数点前只有1位数),那么20.48就该写成2.048×101——这种形式称为数的规格化表示。如此,对于机器而言,它需要存储的是乘号前面的数值和10头上的指数(也称阶码):
此例中,较定点数而言,浮点数所需的存储空间少了。再举个更明显的例子,比如1024+0.000000002048,这一在6位数定点机器根本计算不了的“难题”,却由于0.000000002048可规格化为2.048×10-9,而成为浮点机器的小菜一碟。
发现没有?阶码的本质是小数点在规格化过程中浮动的位数,小数点往左浮动阶码就是正数,往右浮动阶码就是负数。浮点数由此得名。
二进制数也是如此,比如1024的二进制串为10000000000(1后面10个0),规格化表示为1×210(小数点左浮10位)。对了,得把阶码也写成二进制的形式:1×21010。
我们进一步以一个随机的二进制数100111011为例,它的规格化表示为1.00111011×21000(小数点左浮8位)。二进数在规格化后,小数点前总是1,为了节约空间,这一位可以不予存储,只需要存储小数点后的尾数和阶码即可。
在1个字中,祖思为尾数分配了16位的存储空间,为指数分配为了7位,另外留出1位用于表示数的正负(符号位)。因此,Z1的字长为24位。1.00111011×21000在Z1中的存储格式形如:
存储器由3个彼此相同金属片阵列组成,单个字的24位被拆成3段,位于图中左上角的存储器阵列负责存储所有数据的阶码和符号位,另外2个阵列负责存储所有数据的尾数。每个阵列由8层金属片堆叠而成,每一层可存放8个数据段。
综合评价
Z1是世界上第一台二进制可编程计算机,其设计是极富开创性的,其中许多理念都被现代计算机所沿用:
- 将数据存储和指令处理分开,正是现代计算机的做法。
- 奠定了二进制计算的基调,引入了实现二进制计算的基本要素——逻辑门。
- 二进制数的规格化表示简洁而优雅,如今已被纳入IEEE标准。
- 有了明确的机器周期概念,马达每转1圈,负责驱动金属片在4个方向上平移1圈,最终回到原位。加法运算最为简单,耗时1个机器周期;乘法运算最为复杂,耗时20个周期。以完成加法的1个机器周期为例,4次平移分别完成读数、计算部分和、计算进位和计算最终结果。原Z1的工作频率为4Hz,即每秒完成4个机器周期(马达每秒运转4圈);复制品的工作频率仅有1Hz,完成一次乘法运算需要20秒。
可惜的是,尽管祖思的设计看起来精致而优雅,然而不论是1938年的Z1还是1989年的复制品都无法顺利运行,复制品甚至在揭幕仪式上就宕机了,祖思花了好几个月才将它修好。1995年祖思去世之后,这台机器就再也没有运转过,成为一具在博物馆长眠的钢铁尸体。
Z1的后继者们
Z2
Z1的不可靠,很大程度上归咎于机械材料的局限性。简单的机械运动一方面速度不快,另一方面无法灵活、可靠地传动。祖思早有采用电磁继电器的想法,无奈那时的继电器不但价格昂贵,体积还不小。Z1之后,祖思灵机一动:Z1中零件最多的其实是存储器部分,何不保留机械存储器,而把运算和控制部分改用继电器实现呢?
带着这个想法,祖思建造了第2台机器——Z2。
Z2于1940年建成,是一台半机械、半继电器的机电计算机,用到了约600个电磁继电器。为了提高机械存储器的可靠性,祖思将字长缩减至16位,并使用了简单的定点数,但效果仍然并不理想。
继电器的引入和存储字长的缩减大大减轻了机器的重量,总重约300kg。机器的工作频率则提高到了5Hz,计算一次加法仅需约0.8秒。
可惜的是,Z2也毁于Z1遭遇的那场空袭。不过在它建成之际,祖思就及时向德国航空太空中心做了演示,他十分走运,这次演示是Z2为数不多成功运转的一次。德国航空太空中心看到了它的军用价值,当即决定资助这个项目,这才有了完全由继电器构成的第3台祖思机——Z3。
Z3
Z3和Z1的架构完全一致,只是用2000多个电磁继电器替换了原本的机械功能部件。和使用十进制的制表机不同,具有开、合两种状态的继电器在Z3的二进制处理中表现出极高的“天赋”。没有了机械的先天缺陷,Z3的可靠性有了质的飞跃,1941年建成之后就开始服役,用于计算炸弹的空气动力学问题。
不过比起Z1和Z2,Z3更加“短命”,摧毁它的空袭来得更早(1943年12月21日)——Z3“享年”2岁半。
1961年,祖思建造了Z3复制品,藏于德意志博物馆。
不同与Z1复制品,Z3复制品和原Z3一样可靠,至今仍可正常工作。它以5.3Hz的频率工作,一次加法仅需0.8秒,一次乘法仅需3秒,通过指示灯显示结果。它不仅支持四则运算,还可以求平方根。
1998年,来自柏林自由大学的劳尔·罗雅斯(Raúl Rojas)教授证明了Z3的图灵完备性(Turing completeness)。只不过Z3本身不支持循环和分支结构,需要通过手动将穿孔带的两头接起来形成环来实现指令循环,通过数学上的等效来模拟条件分支。
Z4
其实,早在1937年,祖思就已经着手开展了真空电子管的研究。他的搭档赫尔穆特·施赖尔(Helmut Schreyer)也在很早就提出了建造电子计算机的建议,但这个设想在当时的人们眼中简直是天方夜谭。当时的电子设备顶多使用少量的真空管,了解真空管可靠性的行家都清楚地知道,需要成千上万个真空管组成的计算机根本不可能正常运行。就连祖思在一开始也不相信真空管能建造计算机。在施赖尔的坚持下,他们向政府提出了将Z3全面电子化的建议,但政府没有意识到这件事的重大意义,而是在权衡利弊之后,认为机电计算机已经够用了,进一步尝试真空管对战争的意义不大。
于是,祖思的第4台机器——Z4仍然是机电结构的,纳粹德国错过了一次改写历史的机会。
Z4是Z1~Z3的集大成者,是研制时间最长的一型,也是唯一在战争中幸存的一型。1945年,二战已近尾声,2月3日的一场轰炸摧毁了祖思的生产车间,祖思不得不将未完成的Z4从柏林紧急转移至哥廷根。战后的德国元气大伤,直到1949年祖思才得以恢复Z4的工作。1950年7月12日,苏黎世联邦理工学院买下了Z4用于数学和工程研究,Z4成为历史上第二台商业计算机[1],同时也是当时欧洲大陆唯一在役的计算机。
如今,Z4藏于德意志博物馆。它用回了机械存储器,字长扩展到32位,除了四则运算和开平方,还多了求最大、最小值和计算正弦的功能。它弥补了Z3的缺憾,装备了两台穿孔带读取器以实现条件分支(一台读取主程序、一台读取子程序)(原设计中,甚至计划配备6台穿孔带读取器)。它的输出也更多样化,可以打印,也可以(在胶卷上)打孔。
Z4以40Hz的频率工作,一次加法仅需0.4秒,平均每小时可完成约1000次浮点运算。
在Z4的建造过程中,祖思意识到直接使用二进制编程实在太复杂了,于是撰写了一篇博士论文,设计了历史上第一款高级编程语言Plankalkül(Plankalkül在德语中是“Plan Calculus”(计划计算)的意思),并精心编制了一个示例程序——历史上第一个自动下棋程序。Plankalkül在一定程度上启发了后来ALGOL语言的设计,可惜的是,它本身并没有引起足够的重视,这篇论文最终被奥格斯堡大学驳回。
后话
1949年11月8日,祖思成立了一家名为Zuse KG的新公司,将Z系列产品持续迭代至Z43,在1967年被西门子收购之前,共生产了251台计算机。
祖思的晚年荣誉加身,成为德国和世界计算机界公认的祖师级人物。1984年,柏林以他的名字专门设立了一个研究数学和计算机科学的科研机构——柏林祖思研究所(Zuse Institute Berlin/ZIB)。1987年,德国信息学会设立最高奖项“康拉德·祖思奖”,每两年表彰一次国内杰出的计算机学家。
祖思身处的时代,是个计算机研制百花齐放的时代,在那短短几十年里,有太多杰出的计算机先驱在历史上留下自己的名字。和同时期的其他先驱相比,祖思最了不起的地方在于,他几乎是凭借一己之力从零发明了现代计算机,而本书后面将谈到了许多计算机多是由经验丰富专家团队合作研制的。
祖思是幸运的,他生活在最后一个靠单打独斗也能创造传奇的时代,他拥有开明的父母,拥有支持他的朋友,即使是百害而无一利的战争也成为他赢取研究资金的机会,他的晚年功成名就,还有足够多的时间钻研自己的爱好——比如绘画。
祖思也是不幸的,他早年的几乎所有成就都没能引起应有的反响,德国也因此失去了计算机领域的先机。二战期间,柏林作为纳粹政府的首都共遭受了363次空袭,世界反法西斯同盟似乎开了上帝之眼,总能精准打击祖思的辛劳成果。这种不幸也是世界的万幸,著名计算机学者、1974年图灵奖获得者唐纳德·克努特(Donald Knuth)曾提出这样一个思想实验:假如那些摧毁祖思机的空袭没有发生,假如他的博士论文如期发表,世界将会怎样?
参考文献
- Wikipedia. Konrad Zuse[EB/OL].
- Wikipedia. Z1 (computer)[EB/OL].
- Rojas R. The Z1: Architecture and Algorithms of Konrad Zuse's First Computer[J]. Eprint Arxiv, 2014.
- 逸之. Z1:第一台祖思机的架构与算法[EB/OL].
- 柏林自由大学. Konrad Zuse Internet Archive[EB/OL].
- Wikipedia. Z2 (computer)[EB/OL].
- Wikipedia. Z3 (computer)[EB/OL].
- Wikipedia. Z4 (computer)[EB/OL].
- GI. Konrad-Zuse-Medaille-PreisträgerInnen[EB/OL].
-
第一台商业计算机是1949年的电子计算机BINAC,但事实上,它在交付后就没怎么正常运行过。 ↩