力螺旋理论及力封闭抓取的评价指标

---

前言

本文针对抓取任务中的一个关键问题——力封闭（Force closure）展开了较为详尽的叙述。

讲解力封闭前，本文首先介绍了力空间、力螺旋等基础概念，接着引入形封闭、力封闭的概念。

最后，本文介绍了力封闭抓取的评价指标。

1 基础概念

1.1 接触点的力空间

假设现在有这样一个场景（如上图），机械手 $H$ 需要抓取到物体 $B$ ，那么在二者之间必定会产生“接触”。而对于一个手可能有多个手指（两指手、五指手等），因此设有 $n_c$个接触点，第 $i$ 个接触点为 $n_i$ 。

在接触点 $n_i$ 处的力可以分解为：沿着垂直于 $B$ 切平面的轴 $n_i$ 方向（即法线方向）；以及都在切线平面上的另外两个轴方向。

由此，每个接触点的力空间定义为切平面与接触点处法线构成的3D空间。

1.2 刚体运动的力螺旋理论——screw, twist, and wrench

刚体运动是指物体上任意两点之间距离保持不变的运动。机器人运动学、动力学及其控制，实际上就是研究刚体的运动问题。

运⽤力螺旋理论（或者称为旋量理论）来描述刚体运动学问题有两个主要优点：

1. 可以从整体上来描述刚体的运动，这样可以避免用局部坐标系描述时所造成的奇异性，如用欧拉角来描述旋转时这种奇异性就不可避免；
2. 力螺旋理论可以对刚体运动进行几何描述，从而可大大简化对结构的分析。

1.2.1 Screw（旋量运动/螺旋运动）

有如下定理：

• 沙勒定理(Chasles theorem)：刚体的任意运动都可分为平移与旋转的组合。

因此，任意的刚体运动方式都可以用这三个量表达：

1. 轴 $\mathbf{a}$ ，即刚体旋转轴；
2. 角度 $\theta$ ，即刚体绕旋转轴 $\mathbf{a}$ 旋转角度；
3. 位移 $d$ ，即刚体沿旋转轴 $\mathbf{a}$平移位移。

然而，通常不提供位移 $d$ ，而是定义节距（或称螺距） $h=d/\theta$ 。

【旋量运动的定义】

旋量运动的三要素：

1. 轴 $\mathbf{a}$ ，即刚体旋转轴；
2. 节距（或称螺距） $h$ ，即刚体平移位移与绕轴旋转角度的比值（平动与转动的比值）。
3. 大小 $\rho$；

旋量运动表示绕轴 $\mathbf{a}$ 旋转 $\rho =\theta$ ，再沿该轴平移距离为 $h\theta$ 的合成运动。

特例：

• h→∞时，旋量运动是沿旋转轴 $\mathbf{a}$ 距离为 $\rho$ 的纯平移；
• h=0时，旋量运动是绕旋转轴 $\mathbf{a}$ 旋转 $\rho =\theta$ 的纯旋转。

1.2.2 Twist（运动旋量/运动螺旋）

Twist 表示了物体的速度，它是一个六维向量：

$$\mathbf{t}=\left[\begin{array}{c}\mathbf{v}\\ \mathbf{\omega }\end{array}\right]$$

其中， $\mathbf{v}$ 是平移速度， $\mathbf{\omega }$ 是转速。 $\mathbf{v}$ 和 $\mathbf{\omega }$ 都是三维向量。

1.2.3 Wrench（力旋量/力螺旋）

• Wrench的意义：用于表示刚体表面作用力。
• Wrench的定义：

$$F=\left[\begin{array}{c}\mathbf{f}\\ \mathbf{m}\end{array}\right]$$

其中， $\mathbf{f}$ 为力， $\mathbf{m}$ 为力矩。 $\mathbf{f}$ 和 $\mathbf{m}$ 都是三维向量。

1.3 刚体与物体之间的摩擦

1.3.1 无摩擦接触点（ Frictionless contact point）

对于无摩擦接触点，仅考虑fn≥0型的力；fn是沿法线方向的力。

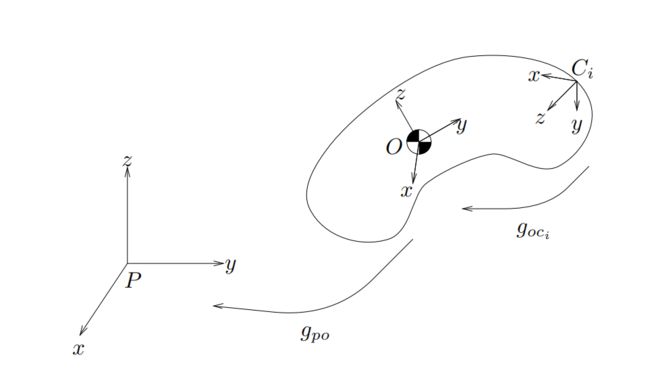
上图展示了一个简单的接触物体模型，图中有三个坐标系——$P$、$O$、$C_i$，他们分别代表了世界坐标系、目标坐标系（通常以质心为原点）以及以第$i$个接触点为原点定义的接触点坐标系。
在接触点坐标系$C_i$中，其力螺旋$F_{c_i}$可以表示为：

$$F_{c_i}=\left[\begin{array}{l}0\\ 0\\ 1\\ 0\\ 0\\ 0\end{array}\right]f_{c_i},f_{c_i}\ge 0$$

式中，$f_{c_i}$ 即$f_n$ 。

显然我们可以注意到，在这个$[6,1]$维的矩阵中前三项仅有第3行为1，后三项均为0。
前者很好理解：对于无摩擦接触仅存在沿法线方向的力；
对于后者，我们需注意到此处公式均考虑于接触点坐标系$C_i$中，而根据力矩的定义（力矩等于力的大小乘以力臂），且接触点处的三个分方向的力臂均为0，因此后三项均为0。

1.3.2 有摩擦接触点（Frictional contact point）

通过上文（1.1 接触点的力空间），我们知道：对于有摩擦接触点，需要考虑沿法线方向的力以及切平面的力。

此时，通过三个分力及其限制条件，可以定义出摩擦锥（ friction cone, FC）：

$$\mathrm{F}\mathrm{C}=\left\{{\left[f_1,f_2,f_n\right]}^T\in {\mathbb{R}}^3\mid \sqrt{f_1^2+f_2^2}\le \mu f_n,f_n\ge 0\right\}$$

上式中 $\sqrt{f_1^2+f_2^2}\le \mu f_n$ 限定了切平面方向的力要满足库伦定律； $f_n\ge 0$ 则限定了法线方向存在大于0的力，即存在沿着法线方向的分力。在这两个条件限制下， $\left[f_1,f_2,f_n\right]$ 构成的力集合在空间中组成了如下图所示的圆锥，即摩擦锥：

在接触点坐标系$C_i$中，其力螺旋$F_{c_i}$可以表示为：

$$\begin{array}{c}{F}_{c_i}=\left[\begin{array}{lll}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]f_{c_i},f_{c_i}\in F{C}_{c_i},\\ F{C}_{c_i}=\left\{f\in {\mathbb{R}}^3:\sqrt{f_1^2+f_2^2}\le \mu f_3,f_3\ge 0\right\}\end{array}$$

式中，$f_3$ 即$f_n$ 。

1.3.3 软接触（Soft contact）

• 软接触相比上述的情况多考虑了扭转力矩；
• 扭转力矩的强度 $\tau$ 满足：

$$\tau \le \gamma f_n$$

式中， $\gamma$ 为扭转摩擦系数。

在接触点坐标系$C_i$中，其力螺旋$F_{c_i}$可以表示为：

$$\begin{gathered} F_{c_i}=\left[\begin{array}{llll}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 1\end{array}\right]f_{c_i},f_{c_i}\in F{C}_{c_i}, \\ F{C}_{c_i}=\left\{f\in {\mathbb{R}}^4:\sqrt{f_1^2+f_2^2}\le \mu f_3,f_3\ge 0,\left|f_4\right|\le \gamma f_3\right\} \end{gathered}$$

式中，$f_3$ 即$f_n$ ，$\left|f_4\right|$ 表示扭转力矩的强度 $\tau$ 。

此外，我们注意到上式矩阵中右下角变为了$1$（即针对扭矩，只有法向分量为1，其余为0），这是为什么呢？

对于考虑于接触点坐标系$C_i$中的软接触情况，只考虑三个方向的力以及沿着法向的扭矩。其中，沿着法向的扭矩并非来自于这三个分力，而是由相当于多点接触的接触面之间扭转导致的。

1.3.4 一般接触情况

基于上述阐述，我们可以用力螺旋基（wrench basis）$B_{c_i}$及摩擦锥$F{C}_{c_i}$建立出表示一般接触情况的数学模型。即：

$$F_{c_i}=B_{c_i}{f}_{c_i}{f}_{c_i}\in F{C}_{c_i}$$

其中，力螺旋基（wrench basis）$B_{c_i}$的维度为 $\left[6\times m\right]$，$m$为接触点力的个数。

总结各类接触类型与对应的力螺旋基以及力的约束，列表如下。其中，第一列是接触类型，第二列是示意图，第三列是力螺旋基，最后一列是力约束条件构成的摩擦锥。

1.4 多指抓取的抓取矩阵

1.4.1 多指抓取的抓取矩阵

前文所讲的力螺旋均是在接触点坐标系下，为了研究多个接触力对物体的影响，我们需要将各个接触力、力螺旋等转换到同一个坐标系——目标坐标系下。

我们用$R_{o{c}_i}$和$p_{o{c}_i}$表示第i个接触点坐标系相对于目标坐标系的RT变换，那么，对于之前分析的每个接触力的力螺旋，我们将其转换到目标坐标系：

$$\begin{array}{rl}{F}_o& ={\mathrm{A}\mathrm{d}}_{g_{o{c}_i}^{-1}}^T{F}_{c_i}\\ & ={\mathrm{A}\mathrm{d}}_{g_{o{c}_i}^{-1}}^T{B}_{c_i}{f}_{c_i}\\ & =\left[\begin{array}{cc}{R}_{o{c}_i}& 0\\ p_{o{c}_i}{R}_{o{c}_i}& R_{o{c}_i}\end{array}\right]B_{c_i}{f}_{c_i},f_{c_i}\in F{C}_{c_i}\end{array}$$

式中，${\mathrm{A}\mathrm{d}}_{g_{o{c}_i}^{-1}}^T$表示从接触点坐标系到目标坐标系下的力螺旋变换矩阵，$p_{oci}$为$p_{oci}$的反对称阵。

反对称阵：$w={\left[\begin{array}{l}x\\ y\\ z\end{array}\right]}^{\wedge }=\left[\begin{array}{rrr}0& -z& y\\ z& 0& -x\\ -y& x& 0\end{array}\right]$

• 有关力螺旋坐标转换矩阵的推导：
  Briot-Khalil2015_Chapter_RepresentationOfVelocitiesAndF.pdf

我们将从接触力$f_{c_i}$到目标坐标系下力螺旋$F_o$的映射矩阵定义为$G_i$：

$$G_i:={\mathrm{A}\mathrm{d}}_{g_{o{c}_i}^{-1}}^T{B}_{c_i}$$

如果有 $k$ 个手指接触到目标物体，那么该物体上总的力螺旋是由于每个手指产生的力螺旋的总和。由于每个接触点的映射矩阵都是线性的，并且力螺旋可以叠加（同一坐标系中），所以目标坐标系下总的力螺旋$F_o$：

$$\begin{array}{rl}{F}_o& =G_1{f}_{c_1}+\cdots +G_k{f}_{c_k}\\ & =\left[\begin{array}{lll}{G}_1& \cdots & G_k\end{array}\right]\left[\begin{array}{c}{f}_{c_1}\\ ⋮\\ f_{c_k}\end{array}\right]\end{array}$$

此时，总的映射矩阵$G$：

$$G=\left[\begin{array}{lll}{\mathrm{Ad}}_{g_{o{c}_1}^{-1}}^T{B}_{c_1}& \cdots & {\mathrm{Ad}}_{g_{o{c}_k}^{-1}}^T{B}_{c_k}\end{array}\right]$$

$$G:{\mathbb{R}}^m\to {\mathbb{R}}^6,m=m_1+\cdots +m_k$$

其维度为 $[6\times m]$，$m$为所有接触点力的个数总和。

由此，我们将多指抓取情况下总的映射矩阵$G$定义为多指抓取的抓取矩阵。

那么基于此，目标坐标系下总的力螺旋$F_o$可以写为：

$$F_o=G{f}_c,f_c\in FC$$

式中，

$$\begin{array}{c}{f}_c=\left(f_{c_1},\dots ,f_{c_k}\right)\in {\mathbb{R}}^m\\ FC=F{C}_{c_1}\times \cdots \times F{C}_{c_k}\subset {\mathbb{R}}^m\\ m=m_1+\cdots +m_k\end{array}$$

至此，可以用抓取矩阵$G$和摩擦锥$FC$完完全全地描述出一个多指抓取了。

1.4.2 多指无摩擦接触

对于每个无摩擦接触点，通过代入无摩擦接触的力螺旋基，得到其力螺旋$F_o$：

$$F_o=\left[\begin{array}{cc}{R}_{o{c}_i}& 0\\ p_{oci}{R}_{o{c}_i}& R_{o{c}_i}\end{array}\right]\left[\begin{array}{l}0\\ 0\\ 1\\ 0\\ 0\\ 0\end{array}\right]f_{c_i}{f}_{c_i}\ge 0$$

通过矩阵乘法运算规则，可将力螺旋$F_o$写为如下形式：

$$F_o=\left[\begin{array}{c}{n}_{c_i}\\ p_{c_i}\times n_{c_i}\end{array}\right]f_{c_i}$$

式中，$n_{c_i}$为目标坐标系下接触面向内的法方向。

对于多个无摩擦接触点，总的力螺旋$F_o$：

$$F_o=\left[\begin{array}{ccc}{n}_{c_1}& \cdots & n_{c_k}\\ p_{c_1}\times n_{c_1}& \cdots & p_{c_k}\times n_{c_k}\end{array}\right]\left[\begin{array}{c}{f}_{c_1}\\ ⋮\\ f_{c_k}\end{array}\right]=G{f}_c,\begin{array}{rl}& F_o\in {\mathbb{R}}^6\\ & f_{c_i}\ge 0\end{array}$$

1.4.3 多指软接触

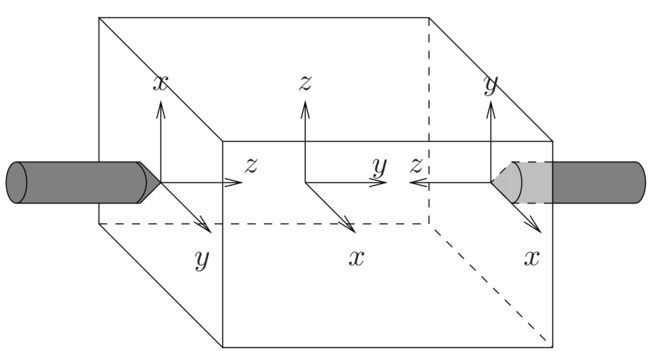
考虑由两个软指握住一个盒子的情况，如下图所示：

两个接触点在目标坐标系的R和T如下：

$$R_{c_1}=\left[\begin{array}{lll}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right]p_{c_1}=\left[\begin{array}{c}0\\ -r\\ 0\end{array}\right]R_{c_2}=\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right]p_{c_2}=\left[\begin{array}{l}0\\ r\\ 0\end{array}\right]$$

对于每个软指，代入 力螺旋基 ，可得每个软指的抓取矩阵：

$$G_i=\left[\begin{array}{cc}{R}_{o{c}_i}& 0\\ p_{oci}{R}_{o{c}_i}& R_{o{c}_i}\end{array}\right]\left[\begin{array}{llll}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$

代入$R_{o{c}_i}$和$p_{o{c}_i}$后得到总的抓取矩阵：

$$G=\left[\begin{array}{cccccccc}0& 1& 0& 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& -1& 0\\ 1& 0& 0& 0& 0& 1& 0& 0\\ -r& 0& 0& 0& 0& +r& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& -1\\ 0& +r& 0& 0& -r& 0& 0& 0\end{array}\right]$$

此外，接触力：

$$f_c=\left(f_{c_1}^1,f_{c_1}^2,f_{c_1}^3,f_{c_1}^4,f_{c_2}^1,f_{c_2}^2,f_{c_2}^3,f_{c_2}^4\right)\in {\mathbb{R}}^8$$

其构成的摩擦锥：

$$\begin{array}{rl}FC& =F{C}_{c_1}\times F{C}_{c_2}\\ F{C}_{c_1}& =\left\{f_c:\sqrt{{\left(f_{c_1}^1\right)}^2+{\left(f_{c_1}^2\right)}^2}\le \mu f_{c_1}^3,\left|f_{c_1}^4\right|\le \gamma f_{c_1}^3,f_{c_1}^3\ge 0\right\}\\ F{C}_{c_2}& =\left\{f_c:\sqrt{{\left(f_{c_2}^1\right)}^2+{\left(f_{c_2}^2\right)}^2}\le \mu f_{c_2}^3,\left|f_{c_2}^4\right|\le \gamma f_{c_2}^3,f_{c_2}^3\ge 0\right\}\end{array}$$

2 形封闭与力封闭（Form closure & Force closure）

在引入力封闭概念之前，我们需要先了解什么是形封闭。毕竟，形封闭一定是力封闭，但反之则不成立。换句话说，形封闭是力封闭的特例。

2.1 形封闭

那么到底什么是形封闭呢？有以下几种说法：

1. 机械手包围住物体时，物体不能移动也不与手碰撞时，就形成了形封闭；
2. 机械手与物体的接触可以防止物体的所有可能的运动，即使是微小的运动；

【形封闭的定义】

首先，定义距离函数表示机械手和物体之间的间隙：

$${\psi }_i(\mathbf{u},\mathbf{q}),1\le i\le n_c$$

其中， $\mathbf{u}$ 和 $\mathbf{q}$ 分别代表了物体和机械手，$n_c$ 为机械手和物体接触点的数目。

那么上式值的正负分别代表了三种情况：

1. 大于0时，即间隙大于0，说明机械手与物体未接触；
2. 等于0时，说明机械手与物体接触了；
3. 小于0时，说明机械手与物体之间发生了渗透。

基于距离函数的定义，可以给出形封闭的定义：

$$\psi (\mathbf{u}+d\mathbf{u},\mathbf{q})\ge 0\Rightarrow d\mathbf{u}=0$$

【上式含义】假设有这种情况：稍微移动物体（物体发生 $d\mathbf{u}$ 的变化），机械手与物体不碰撞渗透（距离函数大于等于0）。求解这个不等式，若得到 $d\mathbf{u}$ 的非零解，表示存在这种情况；反之若仅有$d\mathbf{u}=0$ 的解（物体状态不可变），表示不存在这种情况，即形成了形封闭。

2.2 力封闭

• 何为力封闭？

  如果抓取能够平衡或者抵消施加在物体上的任何外部作用力，即实现力封闭。

• 力封闭定义

  对于任何外力螺旋（例如：重力）${\mathbf{w}}_e$ ，都存在满足摩擦锥约束的接触力向量 $l$ ，使得：

  $$\mathbf{G}\mathbf{l}=-{\mathbf{w}}_e$$

• 力封闭成立的条件

  1. 充分必要条件：

     $$G(FC)={\mathbb{R}}^6$$

     其中，$G(FC)$ 是将抓取映射矩阵G应用于摩擦锥FC中的每个接触力向量 $l$ 所得到的集合。

     【含义】当接触力向量取遍其摩擦锥空间的所有情况时，可以使产生的力螺旋填满整个${\mathbb{R}}^6$ 空间，即可以抵消掉任何外部力。

  2. 必要非充分条件：

     对于任何力封闭情况，其抓取矩阵均需满足行满秩，即：

     $$\mathrm{rank}(\mathbf{G})=6$$

     【含义】仅抓取矩阵行满秩时，才能将力空间（${\mathbb{R}}^3$）完整映射到力螺旋空间（${\mathbb{R}}^6$）。

3. 力封闭抓取的评价指标 Ferrari-Canny Metric

3.1 计算指标前提：力封闭

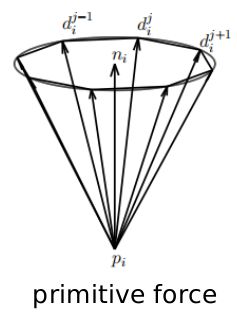
• 力封闭的判断方法：由所有接触点的primitive wrench在力螺旋空间构成的凸包包含零点及其邻域。
• 这里的primitive wrench由primitive force计算力螺旋得到，primitive force是对摩擦锥边界的离散化，如下图所示。

• 因为3D空间中的力螺旋是6维向量（三维的力 + 三维的力矩），无法可视化。因此这里考虑2D空间中的抓取，其力螺旋是3维向量（二维的力 + 一维的力矩），可以通过可视化来直观地了解上述力封闭的判断方法。
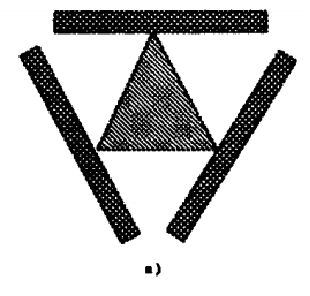
• 如下图是2D平面空间中的一个三指抓取实例，可以看出一共有三个接触点。

• 这个抓取的力螺旋空间及三个接触点的primitive wrench如下图，其中垂直轴对应力矩，两个水平轴对应力。

• 下图是所有primitive wrench构成的凸包，可以看到力螺旋空间的原点在这个凸包内，因此这个抓取是力封闭的。
  

3.2 力封闭抓取的评价指标的定义

• 局部的抓取质量（local grasp quality measure，LQ）指标定义为:

$$L{Q}_{W_e}=\underset{l}{\max }\frac{\Vert W_e\Vert }{\Vert l||}$$

其中，正如上文所讲的，

$$\mathbf{G}\mathbf{l}=-{\mathbf{w}}_e$$

LQ表示外部力螺旋大小和施加的力大小的最大比值，表达了所施加力的有效性。

• 根据局部抓取质量，容易得到全局的抓取质量指标（grasp quality measure，Q）：

$$Q=\underset{w_e}{\min }L{Q}_{w_e}$$

又因为 $\Vert W_e\Vert$ 和 $\Vert l\Vert$ 是线性的，所以不失一般性地，令 $\Vert l\Vert =1$ ，可以得到对应的力螺旋空间 $W_{e,\Vert l\Vert =1}$ ，定义该力螺旋空间为BG。重写LQ和Q的表达式得到：

$$L{Q}_W=\underset{W\in BG}{\max }\Vert W\Vert \to LQ=\Vert w\Vert ,w\in Bd(BG)$$

$$\mathbf{Q}=\underset{w\in Bd(\mathbf{B}\mathbf{G})}{\min }\Vert \mathbf{w}\Vert$$

这里的$Bd(BG)$表示力螺旋空间BG的边界，以及由BG构成的凸包的边界。如下图分别表示2D空间的一个抓取对应的力螺旋空间所构成的凸包，左图对应 $Q_{\infty }$ ，右图对应 $Q_1$，将在下一小节介绍。

3.3 评价指标具体计算

1. $Q_{\infty }$ —— Minimize the max finger force

   其需满足：

   $$\Vert l\Vert \infty =\max \left(l1,.,n\right)=1$$

   $$B\mathcal{G}=W_{L_{\infty }}=W_1\oplus \dots \oplus W_n$$

   $$W_i=\left\{\mathbf{w}i\mid \mathbf{w}i=\sum _{i=1}^m{\alpha }_{i,j}\mathbf{w}i,j,\alpha i,j\ge 0,\sum _{j=1}^m{\alpha }_{i,j}\le 1\right\}$$

   上式中 $\oplus$ 表示闵可夫斯基求和 ，其表征了空间中两个点集求和的所有可能集合，如下图所示：

   

2. 接着将得到的BG代入下式即可：

   $$\mathbf{Q}=\underset{w\in Bd(\mathbf{B}\mathbf{G})}{\min }\Vert \mathbf{w}\Vert$$

3. $Q_1$ —— Minimize the total finger force

   对于 $Q_1$，需要满足：

   $$\Vert l\Vert 1=\mathrm{sum}\left(l1,,,n\right)=1$$

   其对应的BG为：

   $$W_{L_1}=\text{ Convex }\mathrm{Hull}\left(\bigcup _{i=1}^n\left\{\mathbf{w}i,1,\dots ,\mathbf{w}i,m\right\}\right)$$

   同理，代入下式即可：

   $$\mathbf{Q}=\underset{w\in Bd(\mathbf{B}\mathbf{G})}{\min }\Vert \mathbf{w}\Vert$$

参考文献:

[1] Carpin, Stefano, et al. “Multi-fingered robotic grasping: A primer.” arXiv preprint arXiv:1607.06620 (2016).

[2] 摩雷. 机器人操作的数学导论[M]. 机械工业出版社, 1998.

[3] Murray, Richard M., Zexiang Li, and S. Shankar Sastry. A mathematical introduction to robotic manipulation. CRC press, 2017.

[4] Ferrari, Carlo, and John F. Canny. “Planning optimal grasps.” ICRA. Vol. 3. No. 4. 1992.