【机器学习】KNN算法实现鸢尾花分类
文章目录
- 【机器学习】KNN算法实现鸢尾花分类
-
- 1. 概述
- 2. KNN算法的计算过程
-
- 2.1 算法核心
- 2.2 距离计算
- 2.3 k值选择
- 3. KNN实现鸢尾花分类
-
- 3.1 鸢尾花数据集介绍
- 3.2 数据可视化
- 3.3 实现KNN算法的编写
- 3.4 sklearn实现KNN算法
- 4. 讨论
-
- 4.1 KNN算法适用于图像分类吗
- 4.2 KNN算法的优劣
【机器学习】KNN算法实现鸢尾花分类
1. 概述
KNN算法(K-NearestNeighbor)是机器学习领域的基础算法之一,常被用做分类问题与回归问题。
2. KNN算法的计算过程
2.1 算法核心
KNN算法的原理可以总结为"近朱者赤近墨者黑",通过数据之间的相似度进行分类。具体来说,通过计算测试数据和已知数据之间的距离来进行分类。
测试数据的预测结果取决于已知数据和测试数据的距离以及人为设置的k值。如图所示,假设k设置为3,由于测试数据最相近的3个已知数据有2个红色,1个蓝色,则预测结果为红色;假设k设置为5,由于测试数据最相近的5个已知数据又3个蓝色,2个红色,则预测结果为蓝色。
算法流程:
1. 计算预测数据与训练数据之间的距离
2. 将距离进行递增排序
3. 选择距离最小的前K个数据
4. 确定前K个数据的类别,及其出现频率
5. 返回前K个数据中频率最高的类别(预测结果)
两个关键:
1. 距离计算
2. K值选择
2.2 距离计算
已知数据和测试数据的距离有多种度量方式,比如曼哈顿距离,欧式距离,余弦距离等。在KNN算法中常使用的距离计算方式是欧式距离,计算公式如下
二 维 空 间 : ρ = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 n 维 空 间 : d ( x , y ) = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + … + ( x n − y n ) 2 = ∑ i = 1 n ( x i − y i ) 2 二维空间:\\\rho=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ \\ n维空间:\\ d(x, y)=\sqrt{\left(x_{1}-y_{1}\right)^{2}+\left(x_{2}-y_{2}\right)^{2}+\ldots+\left(x_{n}-y_{n}\right)^{2}}=\sqrt{\sum_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2}} 二维空间:ρ=(x2−x1)2+(y2−y1)2n维空间:d(x,y)=(x1−y1)2+(x2−y2)2+…+(xn−yn)2=i=1∑n(xi−yi)2
2.3 k值选择
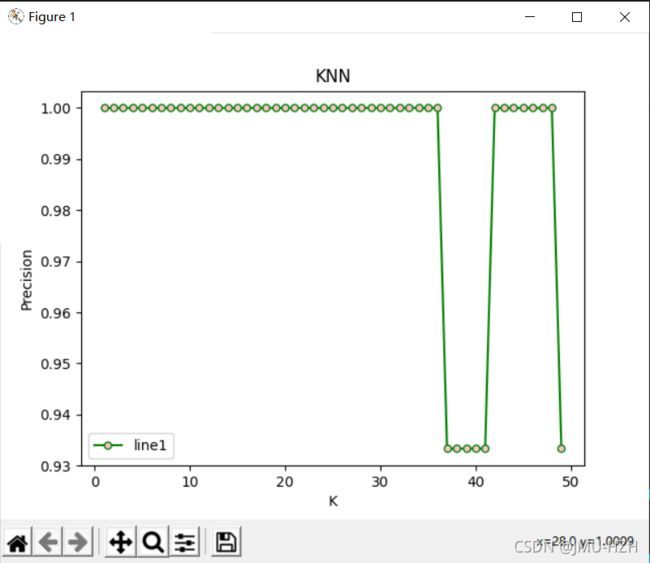
不同的测试数据对k值有不同的要求,因此可以通过交叉验证的方式进行最佳k值的验证。
def cross_define_K(Train, Test, GT):
precision = []
for k in range(1,50):
#print(k)
true = 0
for i in Test:
Test1 = [i[0],i[1],i[2],i[3]]
result = KNN(Train,Test1,GT,k)
collection = Counter(result)
result = collection.most_common(1)
if result[0][0] == i[4]:
true += 1
success = true / len(Test)
precision.append(success)
k1 = range(1,50)
plt.plot(k1,precision,label='line1',color='g',marker='.',markerfacecolor='pink',markersize=10)
plt.xlabel('K')
plt.ylabel('Precision')
plt.title('KNN')
plt.legend()
plt.show()
3. KNN实现鸢尾花分类
3.1 鸢尾花数据集介绍
鸢尾花数据集记录了三类花以及它们的四种属性。(四种属性:花萼长度,花萼宽度,花瓣长度,花瓣宽度;3种标签:Setosa,versicolor,virginica)。我们的目标是当输入一个测试数据时通过KNN算法获得预测结果。

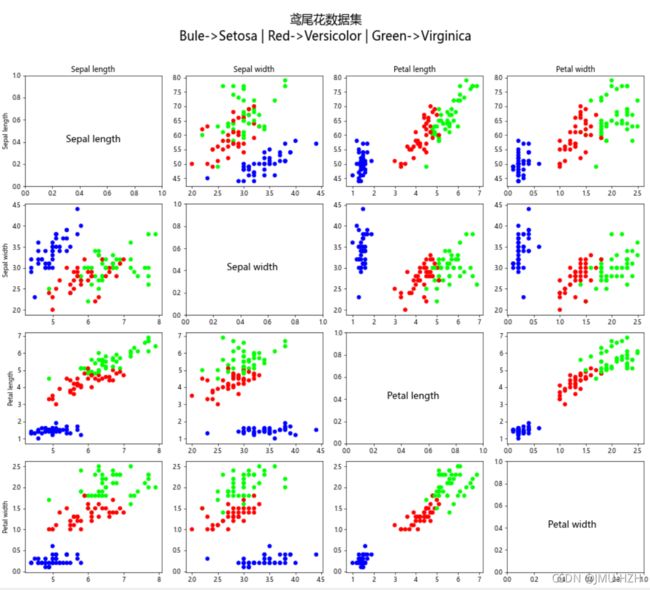
3.2 数据可视化
我们可以提取鸢尾花的任意两个特征作为二维空间的坐标点进行可视化,来观察每个类别的属性分布范围。
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import pandas as pd
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
TRAIN_URL = r'http://download.tensorflow.org/data/iris_training.csv'
train_path = tf.keras.utils.get_file(TRAIN_URL.split('/')[-1],TRAIN_URL)
names = ['Sepal length','Sepal width','Petal length','Petal width','Species']
df_iris = pd.read_csv(train_path,header=0,names=names)
iris_data = df_iris.values
plt.figure(figsize=(15,15),dpi=60)
for i in range(4):
for j in range(4):
plt.subplot(4,4,i*4+j+1)
if i==0:
plt.title(names[j])
if j==0:
plt.ylabel(names[i])
if i == j:
plt.text(0.3,0.4,names[i],fontsize = 15)
continue
plt.scatter(iris_data[:,j],iris_data[:,i],c= iris_data[:,-1],cmap='brg')
plt.tight_layout(rect=[0,0,1,0.9])
plt.suptitle('鸢尾花数据集\nBule->Setosa | Red->Versicolor | Green->Virginica', fontsize = 20)
plt.show()
3.3 实现KNN算法的编写
KNN算法的思想基本围绕距离计算和k值选择。建议大家都可以自己手写一份,具体细节已在代码中注释。
import numpy as np
import pandas as pd
import math
from collections import Counter
import matplotlib.pyplot as plt
# 读取数据集
def Data():
iris=pd.read_csv('iris.csv')
return iris
# 划分数据集
def Datasets(iris):
index=np.random.permutation(len(iris))
index=index[0:15]
Test = iris.take(index)
Train = iris.drop(index)
datasets = [Test, Train]
return datasets
# KNN算法
def KNN(Train, Test, GT, k):
Train_num = Train.shape[0]
tests = np.tile(Test, (Train_num, 1)) - Train
distance = (tests ** 2) ** 0.5
result = distance.sum(axis=1)
results = result.argsort()
label = []
for i in range(k):
label.append(GT[results[i]])
return label
def cross_define_K(Train, Test, GT):
precision = []
for k in range(1,50):
#print(k)
true = 0
for i in Test:
Test1 = [i[0],i[1],i[2],i[3]]
result = KNN(Train,Test1,GT,k)
collection = Counter(result)
result = collection.most_common(1)
if result[0][0] == i[4]:
true += 1
success = true / len(Test)
precision.append(success)
k1 = range(1,50)
plt.plot(k1,precision,label='line1',color='g',marker='.',markerfacecolor='pink',markersize=10)
plt.xlabel('K')
plt.ylabel('Precision')
plt.title('KNN')
plt.legend()
plt.show()
if __name__ == "__main__":
# 读取iris数据集
iris = Data()
# 对数据集进行划分(训练集,测试集)
datasets = Datasets(iris)
print(datasets[0])
# 设置KNN的k值
k = 3
# 将训练集的GT隐去
Train = datasets[1].drop(columns=['class']).values
# 读取训练集的GT
GT = datasets[1]['class'].values
# 读取测试集
Test = datasets[0].values
cross_define_K(Train,Test,GT)
true = 0
for i in Test:
Test = [i[0],i[1],i[2],i[3]]
result = KNN(Train,Test,GT,k)
# KNN返回的是测试数据与训练数据相近的n个预测值
collection = Counter(result)
result = collection.most_common(1)
#print(result[0][0])
# 选取其中出现最多的结果进行验证
if result[0][0] == i[4]:
true += 1
success = true/len(datasets[0])
print('success:\n',success)
3.4 sklearn实现KNN算法
sklearn也封装好了KNN算法,可以直接运行。
import sklearn.datasets as datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
iris = datasets.load_iris()
feature = iris['data']
target = iris['target']
x_train, x_test, y_train, y_test = train_test_split(feature, target, test_size=0.2, random_state=2021)
print(x_train)
knn = KNeighborsClassifier(n_neighbors=3)
knn = knn.fit(x_train, y_train)
print(knn)
y_pred = knn.predict(x_test)
y_true = y_test
print('模型的分类结果:', y_pred)
print('真实的分类结果:', y_true)
print(knn.score(x_test, y_test))
test1 = knn.predict([[6.1, 3.1, 4.7, 2.1]])
print(test1)
4. 讨论
4.1 KNN算法适用于图像分类吗
KNN算法是手写体识别任务的解决方案之一,但是实际的图像分类基本不会用到KNN算法。
首先测试图像需要和大量训练图像进行比较,因此测试需要花费一定的时间,其次图像是高维度数据,表达的是丰富的语义信息,无法通过简单的像素距离进行分类。
而KNN算法应用于手写体识别有两个原因,首先minist数据集的是单通道图像,将会减少一定的测试时间,其次minsit数据集语义信息简单,KNN算法的测试偏差不会太大。
4.2 KNN算法的优劣
优势:
1. 思想简单,简洁明了
2. 对异常值不敏感
3. 输入数据限制小
4. 精度高
劣势:
1. 计算复杂度高
2. 预测速度缓慢
3. 受数据规模影响敏感