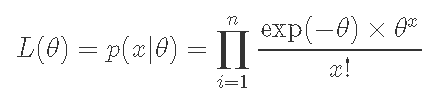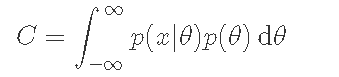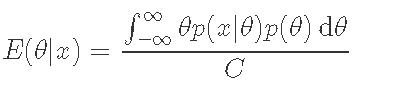拓端tecdat|R语言贝叶斯Poisson泊松-正态分布模型分析职业足球比赛进球数
原文链接：http://tecdat.cn/?p=23099
原文出处：拓端数据部落公众号
在本文关于如何在R中进行贝叶斯分析。我们介绍贝叶斯分析，这个例子是关于职业足球比赛的进球数。
模型
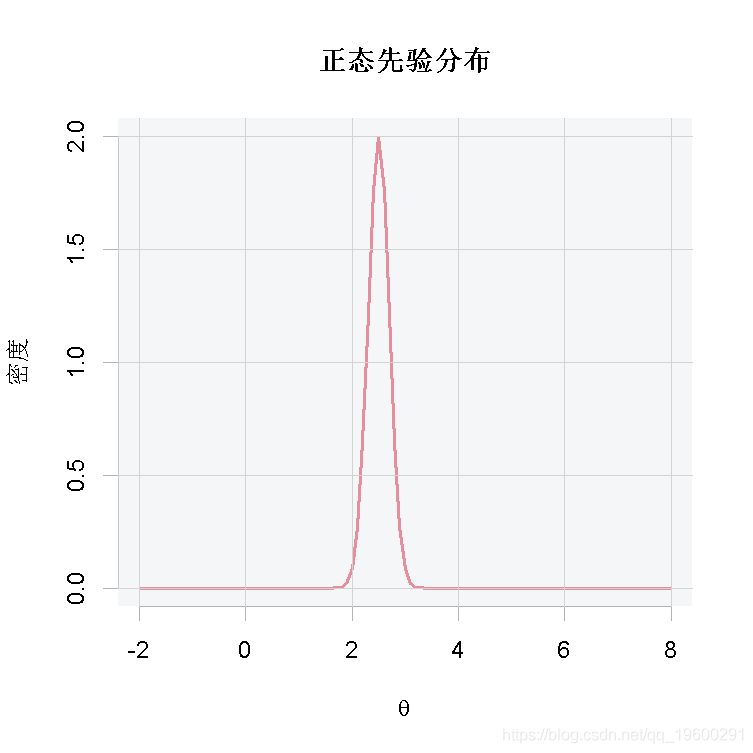
首先，我们认为职业足球比赛的进球数来自分布
，其中θ是平均进球数。现在假设我们用一位足球专家的意见来得出足球比赛的平均进球数，即参数θ，我们得到：
。
curve(dnorm(x, 2.5, 0.2), from = -2, to = 8,...) 
我们想知道什么？
在这种情况下，我们想知道θ的后验分布是什么样子的，这个分布的平均值是什么。为了做到这一点，我们将在三种情况下分析：
我们有1个观察值x=1，来自分布为
的总体。
我们有3个观测值x=c(1,3,5)，来自一个具有分布的总体。
我们有10个观测值x=c(5,4,3,4,3,2,7,2,4,5)，来自一个具有分布的总体。
理论方法
在这里，我想告诉你贝叶斯分析是如何分析的。首先，我们有一个来自具有未知参数θ的泊松分布的人口的似然函数。
我们知道参数θ的先验分布p(θ)是由以下公式给出的。
最后，θ的后验分布为。
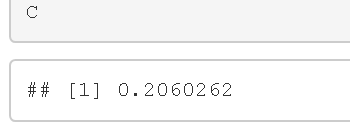
其中常数C的计算方法如下。
而后验分布E(θ|x)的平均值由以下公式给出。
计算方法
在这里，你将学习如何在R中使用蒙特卡洛模拟来回答上面提出的问题。对于这三种情况，你将遵循以下步骤。
1. 定义数据
首先，你需要根据方案定义数据。
x <- 1 #第一种情况2. 计算常数C
现在使用蒙特卡洛模拟来计算积分。为此，有必要从先验分布中产生N=10000个值θi，并在似然函数
中评估它们。最后，为了得到C，这些值被平均化。R中的代码如下。
N <- 100000 # 模拟值的数量
rnorm(n=N, mean = 2.5, sd = 0.2) #先验分布
prod(dpois(x=x, lambda = theta)) #似然函数
3. 寻找后验分布
计算完C后，你可以得到后验分布，如下所示。
fvero(theta) * dnorm(x=theta) / C
4. 计算后验分布的平均数
最后你可以使用蒙特卡洛模拟计算积分来获得后验分布的平均值。
integral <- mean(aux)
posterior <- integral/C
结果
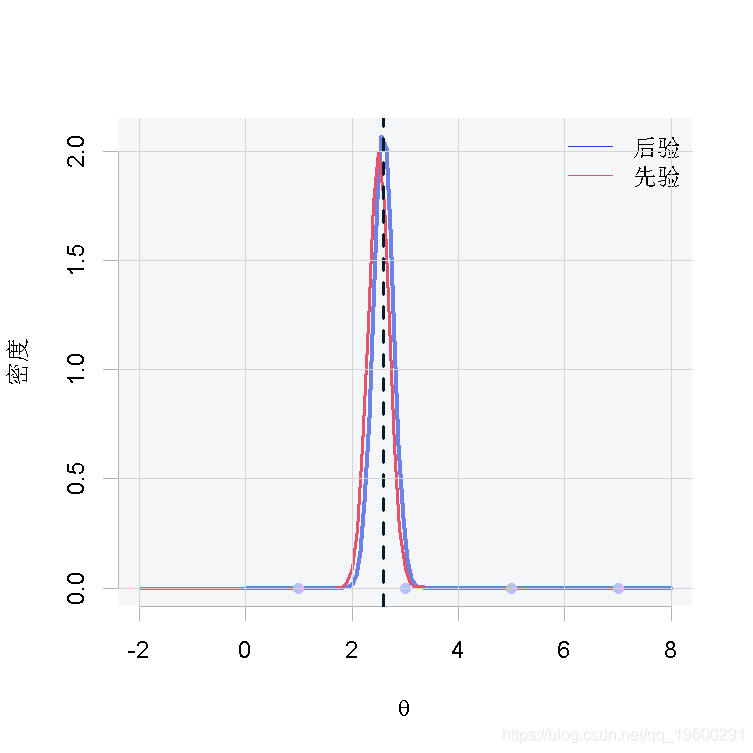
如前所述，上面介绍的代码用于所有三种情况，唯一根据情况变化的是x。在这一节中，我们将为每种情况展示一张图，其中包含θ的先验和后验分布、后验分布的平均值（蓝色虚线）和观测值（粉红色的点）。
第一种情况
curve(dnorm(x, 2.5, 0.2), col=4,,x=x, y=rep(0, length(x)),
line,v = mposterior,legend=c("topright", legend=c("后验", "先验"),)
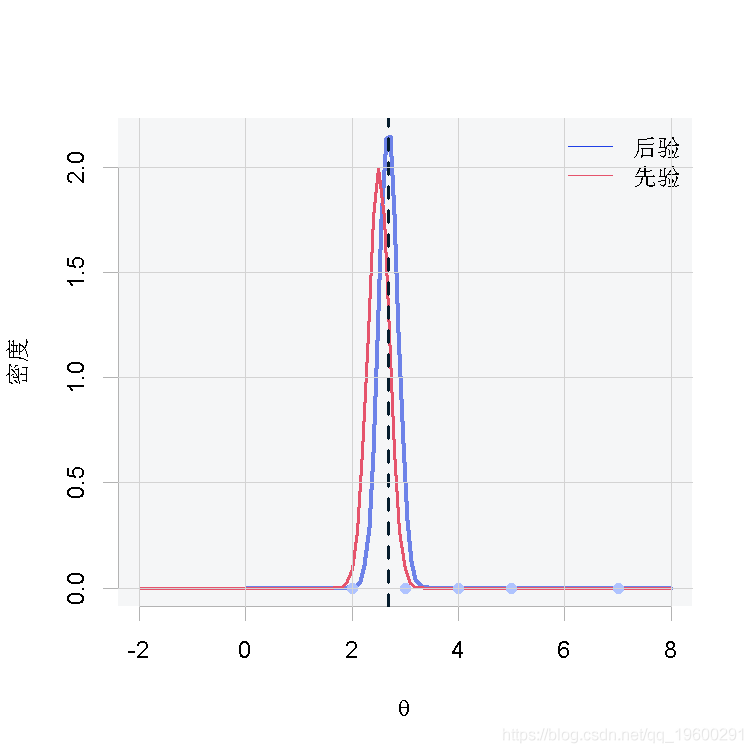
第二种情况
第三种情况
结论
从结果中我们可以得出这样的结论：当我们有很少的观测数据时，如图1和图2，由于缺乏样本证据，后验分布将倾向于类似于先验分布。相反，当我们有大量的观测数据时，如图3，后验分布将偏离先验分布，因为数据将有更大的影响。
我希望你喜欢这篇文章并了解贝叶斯统计。我鼓励你用其他分布运行这个程序。
最受欢迎的见解
1.R语言多元Logistic逻辑回归 应用案例
2.面板平滑转移回归(PSTR)分析案例实现
3.matlab中的偏最小二乘回归（PLSR）和主成分回归（PCR）
4.R语言泊松Poisson回归模型分析案例
5.R语言回归中的Hosmer-Lemeshow拟合优度检验
6.r语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现
7.在R语言中实现Logistic逻辑回归
8.python用线性回归预测股票价格
9.R语言如何在生存分析与Cox回归中计算IDI，NRI指标