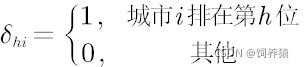[刨根问底] 五分钟搞懂组合评价模型—模糊Borda (以2021 年大学生数模国赛C题为例)
组合评价模型—模糊Borda(Matlab)
我们的征途是星辰大海,而并非烟尘人间。
目录
组合评价模型—模糊Borda(Matlab)
一、模糊Borda法简介
二、模糊Borda法主要步骤
(1)计算隶属度
(2)计算模糊频数
(3)计算模糊频率
(4)将排序转化为得分
(5)计算模糊Borda数FBi,FBi值越大,名次越靠前
三、案例分析(2021 年高教社杯全国大学生数学建模竞赛C题)
(1)案例分析
(2)代码实现
第一步:计算隶属度
第二步:计算模糊频数
第三步:计算频率,也就是归一化
第四步:将排序转化为得分
第五步:计算模糊Borda数FBi,然后输出排名
四、总结
(1)模糊Borda优点
(2)模糊Borda缺点
一、模糊Borda法简介
Borda法是由C·de Borda在1784年提出的,最早是为了解决投片选举问题。其基本思想是:通过比较 m 位评价者所给出的对 n 个被评价对象的优序关系,最终确定 n 个被评价对象的Borda分,以Borda分为大小从高到低排序。
案例一:
设一个选举有三个候选人甲、乙、丙,结果如下:
4 张选票为:甲 > 乙 > 丙;
5 张选票为:甲 > 丙 > 乙;
7 张选票为:丙 > 乙 > 甲。
按简单多数规则 s1 = 1, s2 = s3 = 0,则甲 9 票,乙 0 票,丙 7 票。结果是甲当选。由于没有选民把乙排第一,所以当选的不是甲就是丙,取决于谁的支持者多。这体现了简单多数规则的弊端——较易选出极端或争议人士,可能会让 51% 的人最满意,而无视 49% 的人的利益。
按线性波达数规则 s1 = 2, s2 = 1, s3 = 0,则甲 18 分,乙 11 分,丙 19 分。结果是丙当选。造成这一结果的原因可能是甲的 9 名支持者采用的是真诚选举,如实表达自己的偏好顺序,而丙的 7 名支持者采用的是策略选举,一致将甲排在最后。
可见要寻找一个好的投票规则并不容易。如果采用瑙鲁议会规则,s1 = 1, s2 = 1/2, s3 = 1/3,则甲 11.33 分,乙 7.17 分,丙 10.83 分。结果是甲当选。瑙鲁议会规则将反对者的声音控制在一人一分以内,限制了策略选举的影响。
组合评价就是将多个评价方法的结果再算一下,得到一个更有参考价值的结果,但是要求几种评价方法的结果相似,比如对几个供应商重要性进行排名,首先通过了秩和比、topsis法等算法算出评价值,这些评价值作为Borda的初始数据。关于评价方法,不一定都是客观的方法,一些主观的方法都是可以的,确定判断矩阵时应结合实际考虑。
二、模糊Borda法主要步骤
Borda法分为以下五个步骤:
(1)计算隶属度
![]() 可以表示为第i个供应商第j种评价方法的结果,其实这里呢就是一个简单的归一化,在一些运算过程中,趋向于0的值可能导致当此相乘的结果接近零,可能会影响到结果,这里我们可以把上式改为最低值为0.1:
可以表示为第i个供应商第j种评价方法的结果,其实这里呢就是一个简单的归一化,在一些运算过程中,趋向于0的值可能导致当此相乘的结果接近零,可能会影响到结果,这里我们可以把上式改为最低值为0.1:
(2)计算模糊频数
![]() 矩阵根据评价结果构建0,1矩阵,然后带入进行运算
矩阵根据评价结果构建0,1矩阵,然后带入进行运算
(3)计算模糊频率
(4)将排序转化为得分
![]() 为供应商i在h位的得分,这里的
为供应商i在h位的得分,这里的![]() 指对象个数,如果要对比402家供应商那么这里的
指对象个数,如果要对比402家供应商那么这里的![]()
(5)计算模糊Borda数FBi,FBi值越大,名次越靠前
三、案例分析(2021 年高教社杯全国大学生数学建模竞赛C题)
(1)案例分析
第一问要求我们确定50家最重要的供应商,一般的都是从供应情况去看,这里可以确定一些指标,然后进行评价,最后评分最高Top50作为本问结果,可以考虑以下指标:
(1)材料性价比:计算各原材料经济效益,1/[0.6 0.66 0.72]=[1.67 1.52 1.39],然后再去除下单价,[1.67 1.52 1.39]/[1.2 1.1 1]=[1.3889 1.3774 1.3889],各供应商按供应的原材料对应,将这个结果作为第一个指标,为正向指标,指标越大越好。
(2)供应商最大供应能力:最大供应量并换算为产能,为正向指标,指标越大越好
(3)供应商平均供应能力:平均供应量并换算为产能,为正向指标,指标越大越好
(4)历史供应量/历史订单量比,为正向指标,指标越大越好
(5)供应商供应可靠性,对历史供应数据,做方差分析,为负向指标,指标越小越好
(6)企业平均需求:企业平均需求可用于衡量该生产企业在每个供应商的订货量总体水平。观察附件1中数据,可发现存在大量为0的数据,故对每个供应商的订货量进行求和,可以在保证计算结果正确的同时排除0数据的干扰。将每个供应商在240周的订货量进行求和,再除以有订货的周数,得到企业平均需求。
除了以上指标大家还可以多增加一些,然后用评价算法评价后排序即可,第一问评价可以用多种算法例如投影寻踪、熵权法、Tosis等评价,然后在通过组合评价方法例如Borda求一个综合性的评价值,然后进行排序。
(2)代码实现
第一步:计算隶属度
x=[ ]; %x矩阵储存各评价方法的得分,一行代表一家供应商,列代表不同的评价方法
Ma = max(x,[],2); %求每列最大值
Mi = min(x,[],2); %求每列最小值
for i = 1:402 %402家供应商
for j = 1:N %N种评价方法,记得把N改为你自己选择的评价方法数,不然会报错
u(i,j) = ((x(i,j)-Mi(i,1))./(Ma(i,1)-Mi(i,1))).*0.9+0.1;
end
end第二步:计算模糊频数
B=zeros(402,402);%储存模糊频数矩阵
BB1=();%储存第一种评价方法排名
BB2=();%储存第二种评价方法排名
%求模糊频数矩阵
for i=1:402
B(i,BB1(i,1))=1;
end
for j=1:402
B(j,BB2(j,1))=1;
end第三步:计算频率,也就是归一化
%计算模糊频率
for h = 1 : 402
for i = 1 : 402
p(h,i) = sum(B(h,i) .* u(i,:));
end
end
for h = 1 : 402
for i = 1 : 402
w(h,i) = p(h,i) ./ sum(p(:,i));
end
end
第四步:将排序转化为得分
%计算最终得分
for h = 1 : 402
for i = 1 : 402
Q(h,i) = 0.5 * (402- h) * (402 - h + 1);
end
end
Q=Q';第五步:计算模糊Borda数FBi,然后输出排名
%计算模糊Borda数FBi,然后输出排名
FB = sum(w.*Q,2);
[a,PX]=sort(FB(end:-1:1));
[xx2,yy2]=sort(PX);%将排名与序号对应(按照排名升序)(xx2为排名,yy2为序号)
PM=zeros(402,2);
PM(:,1)=yy2;
PM(:,2)=xx2;
Top=[];
Top=yy2(1:50,1);以上就是小编国赛C题第一问的求解过程啦~,小编用的是比较简单的方法,由于时间比较紧,比赛的时候只选用了两种评价方法,再用模糊Borda组合评价求解,得到三个结果,再分别计算匹配度,最后选择最好的那个在论文上重点着墨。
四、总结
(1)模糊Borda优点
模糊Barda法可以综合多种评价方法的不同结果,该方法既考虑不同方法下排序名次的差异,又考虑相应评价方法下各项目的得分值,能更好地利用已有的评价信息,从而使得评价结果具有较高的合理性和优越性。
(2)模糊Borda缺点
模糊Borda法冠名为“模糊”的理由是,计算了所谓的“隶属度”。其实,![]() 只不过是实际评价值的一个区间线性变换(极差变换或极大值相对化变换)。通过变换之后,所有的评价方法输出值的取值区间均为[0,1]。它充其量也只是“评语等级退化为单个等级”时的隶属度,或者称为“隶属优度”,从整个过程来看,该方法并没有与模糊数学中的有关运算规则、特殊概念发生很强的联系。
只不过是实际评价值的一个区间线性变换(极差变换或极大值相对化变换)。通过变换之后,所有的评价方法输出值的取值区间均为[0,1]。它充其量也只是“评语等级退化为单个等级”时的隶属度,或者称为“隶属优度”,从整个过程来看,该方法并没有与模糊数学中的有关运算规则、特殊概念发生很强的联系。
在学习中成功、在学习中进步!我们一起学习不放弃~
记得三连哦~mua 你们的支持是我最大的动力!!欢迎大家阅读往期文章哈~
小编联系方式如下,欢迎各位巨佬沟通交流。
print("QQ:1654243128")![]()
![[刨根问底] 五分钟搞懂组合评价模型—模糊Borda (以2021 年大学生数模国赛C题为例)_第1张图片](http://img.e-com-net.com/image/info8/bfd6ec670c2148e292347451b444a489.jpg)
![[刨根问底] 五分钟搞懂组合评价模型—模糊Borda (以2021 年大学生数模国赛C题为例)_第2张图片](http://img.e-com-net.com/image/info8/94e7e6f75c2645cb9e1f14794ce4ee02.jpg)
![[刨根问底] 五分钟搞懂组合评价模型—模糊Borda (以2021 年大学生数模国赛C题为例)_第3张图片](http://img.e-com-net.com/image/info8/2162e462e1144f9e88a93a281cf87fd6.jpg)
![[刨根问底] 五分钟搞懂组合评价模型—模糊Borda (以2021 年大学生数模国赛C题为例)_第4张图片](http://img.e-com-net.com/image/info8/9920d5f1e9a04baf8f0df5a15caf4660.jpg)
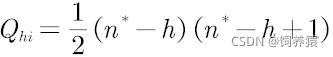
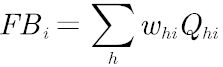
![[刨根问底] 五分钟搞懂组合评价模型—模糊Borda (以2021 年大学生数模国赛C题为例)_第5张图片](http://img.e-com-net.com/image/info8/71129d7d2c424c40a190d20f0ed8e523.jpg)