Python-Matplotlib可视化(9)——精通更多实用图形的绘制
Python-Matplotlib可视化(9)——精通更多实用图形的绘制
-
- 前言
- 可视化二维数组的内容
- 为图形添加色彩映射图例
- 二维标量场的可视化
- 等高线的可视化
- 二维向量场的可视化
- 系列链接
前言
Matplotlib是Python的绘图库,它提供了一整套和 matlab 相似的命令 API,可以生成你所需的出版质量级别的图形。我们已经学习了一系列统计图来描绘两个变量间的基本关系,同时也学习了如何高度自定义统计的呈现样式,但是,仅仅使用这些图形并不足以应对所有场景。例如,我们需要可视化地显示降雨在各个地区的分布情况。 因此,我们需要更多的实用图形来表达现实世界的复杂关系。
可视化二维数组的内容
让我们从最简单的场景开始,假设我们有一个二维数组——著名的分形形状Mandelbrot,我们想将其可视化。
首先需要创建一个二维数组,然后调用plt.imshow()将其可视化。
import numpy as np
import matplotlib.cm as cm
from matplotlib import pyplot as plt
def iter_count(c, max_iter):
x = c
for n in range(max_iter):
if abs(x) > 2.:
return n
x = x ** 2 + c
return max_iter
n = 512
max_iter = 64
xmin, xmax, ymin, ymax = -2.2, .8, -1.5, 1.5
x = np.linspace(xmin, xmax, n)
y = np.linspace(ymin, ymax, n)
z = np.empty((n, n))
for i, y_i in enumerate(y):
for j, x_j in enumerate(x):
z[i, j] = iter_count(complex(x_j, y_i), max_iter)
plt.imshow(z, cmap = cm.Spectral)
plt.show()

Tips:imshow()接受一个2D数组作为参数置,用于渲染图片,其中每个像素代表一个从2D数组中提取的值。像素的颜色从colormap中选取。2D数组中的数据也可以是自文件或其他源,例如我们完全可以将读取的图片绘制在图形中。
import matplotlib.cm as cm
from matplotlib import pyplot as plt
# 读取图片
img = plt.imread('img.png')
# 绘制图片
plt.imshow(img)
plt.show()
 我们也可以使用不同的颜色映射观察效果,只需要修改
我们也可以使用不同的颜色映射观察效果,只需要修改plt.imshow()可选参数cmap的值即可.
plt.imshow(z, cmap = cm.binary, extent=(xmin, xmax, ymin, ymax))
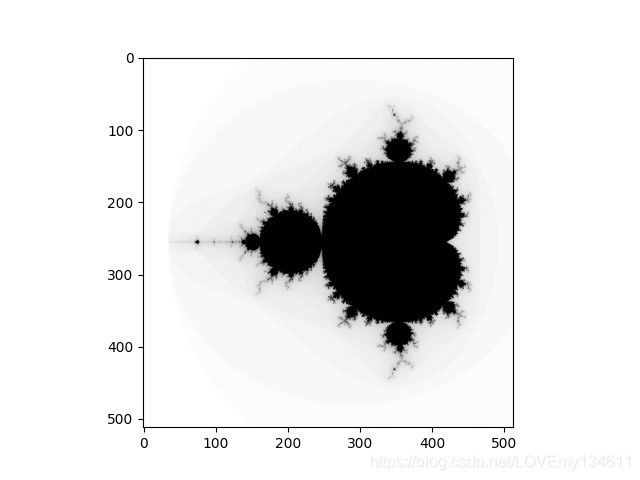
Tips:plt.imshow()的可选参数extent指定存储在二维数组中的数据的坐标系——由四个值组成的元组,分别表示水平轴和垂直轴上的最小、最大范围。
接下来,将数组的尺寸由从512x512减少到32x32,看看效果如何:
n = 64
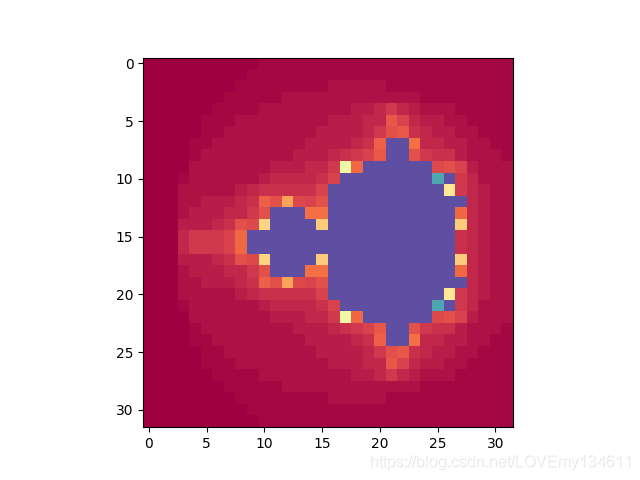
Tips:使用32x32的数组表示Mandelbrot集时,得到的图片的尺寸并没有缩小,但和512x512数组产生的图片仍有明显差别。这是由于,生成一张给定大小的图片,如果输入的数据小于或大于该图片尺寸,plt.imshow()将执行插值操作。默认的插值是线性插值,可以看出效果并不总是理想的。可以通过imshow()函数的可选参数interpolation指定要使用的插值类型。
使用双三次插值算法(interpolation = ‘bicubic’)查看效果:

为图形添加色彩映射图例
使用色彩映射可以绘制可读性和视觉性都较好的图形,当使用色彩映射时,我们就可以大致知道相应颜色对应的值。
import numpy as np
import matplotlib.cm as cm
from matplotlib import pyplot as plt
def iter_count(c, max_iter):
x = c
for n in range(max_iter):
if abs(x) > 2.:
return n
x = x ** 2 + c
return max_iter
n = 512
max_iter = 64
xmin, xmax, ymin, ymax = -2.2, .8, -1.5, 1.5
x = np.linspace(xmin, xmax, n)
y = np.linspace(ymin, ymax, n)
z = np.empty((n, n))
for i, y_i in enumerate(y):
for j, x_j in enumerate(x):
z[i, j] = iter_count(complex(x_j, y_i), max_iter)
plt.imshow(z, cmap = cm.Spectral, interpolation='bicubic')
cb = plt.colorbar(orientation='horizontal', shrink=.75)
cb.set_label('colormaping')
plt.show()

Tips:plt.colorbar()函数向Matplotlib发出信号显示一个colorbar。其中:可选参数orientation用于选择颜色栏是垂直还是水平,默认情况下,它是垂直的;shrink参数用于缩放颜色栏。调用plt.colorbar()函数将生成一个Colorbar实例,调用该Colorbar实例的set_label()方法,可以为颜色栏设置标题。
二维标量场的可视化
可以使用numpy.meshgrid() 函数从2D函数中生成样本。然后,使用plt.pcolormesh()显示此函数图形:
import numpy as np
import matplotlib.cm as cm
from matplotlib import pyplot as plt
n = 256
x = np.linspace(-3., 3., n)
y = np.linspace(-3., 3., n)
x_list, y_list = np.meshgrid(x, y)
z_list = x_list * np.cos(x_list ** 2 + y_list ** 2)
plt.pcolormesh(x_list, y_list, z_list, cmap = cm.Spectral)
cb = plt.colorbar(orientation='horizontal', shrink=.75)
plt.show()

Tips:使用颜色映射可以帮助我们快速判断相应点的符号和大小。
np.meshgrid()函数的作用是:获取两个坐标列表,并构建坐标网格。因为两个坐标列表都是numpy数组,所以我们可以以处理单个变量的方式处理它们,这使得计算标量场的过程简洁易读。最后,调用函数plt.pcolormesh()呈现图片。
等高线的可视化
等高线将具有相同值的所有点连接起来,可以更容易看到数据的分布特征。
import numpy as np
from matplotlib import pyplot as plt
import matplotlib.cm as cm
def iter_count(c, max_iter):
x = c
for n in range(max_iter):
if abs(x) > 2.:
return n
x = x ** 2 + 0.98 * c
return max_iter
n = 512
max_iter = 80
xmin, xmax, ymin, ymax = -0.32, -0.22, 0.8, 0.9
x = np.linspace(xmin, xmax, n)
y = np.linspace(ymin, ymax, n)
z = np.empty((n, n))
for i, y_i in enumerate(y):
for j, x_j in enumerate(x):
z[j, i] = iter_count(complex(x_j, y_i), max_iter)
plt.imshow(z, cmap = cm.Spectral,
interpolation = 'bicubic',
origin = 'lower',
extent=(xmin, xmax, ymin, ymax))
levels = [8, 12, 16, 20]
ct = plt.contour(x, y, z, levels, cmap = cm.binary)
plt.clabel(ct, fmt='%d')
plt.show()

Tips:pyplot.contour()函数获取样本网格的坐标列表x和y以及存储在矩阵z中的值。然后,该函数将渲染在"level"列表中指定的值相对应的轮廓,可以使用可选参数cmap运用色彩映射进行着色,也可以使用可选参数color为所有轮廓指定一种唯一的颜色。
每个轮廓可以用颜色条显示,也可以直接在图形上显示。plt.contour()函数返回一个Contour实例。pyplot.clabel()函数获取contour实例和一个可选的格式字符串来呈现每个等高线的标签。
Tips:默认情况下,填充轮廓不具抗锯齿性。可以使用了可选参数antialiased来获得更令人满意的结果。
ct = plt.contour(x, y, z, levels, cmap = cm.binary, antialiased = True)
二维向量场的可视化
向量场将二维向量与二维平面的每个点相关联,在物理学中很常见。
本例中,为了进行符号计算,我们借助SymPy包,这个软件包只用于保持代码的简短。如果未安装此包,可以使用pip install sympy命令进行安装。
我们不必关系向量场的计算方法,记住,本文的主要目的是可视化,因此我们只需要关心如何显示向量场——使用pyplot.quiver()函数。
import numpy as np
import sympy
from sympy.abc import x, y
from matplotlib import pyplot as plt
import matplotlib.patches as patches
def cylinder_stream_function(u = 1, r = 1):
radius = sympy.sqrt(x ** 2 + y ** 2)
theta = sympy.atan2(y, x)
return u * (radius - r ** 2 / r) * sympy.sin(theta)
def velocity_field(psi):
u = sympy.lambdify((x, y), psi.diff(y), 'numpy')
v = sympy.lambdify((x, y), -psi.diff(x), 'numpy')
return u, v
u_func, v_func = velocity_field(cylinder_stream_function() )
xmin, xmax, ymin, ymax = -2.5, 2.5, -2.5, 2.5
y, x = np.ogrid[ymin:ymax:16j, xmin:xmax:16j]
u, v = u_func(x, y), v_func(x, y)
m = (x ** 2 + y ** 2) < 1.
u = np.ma.masked_array(u, mask = m)
v = np.ma.masked_array(v, mask = m)
shape = patches.Circle((0, 0), radius = 1., lw = 2., fc = 'w', ec = 'c', zorder = 0)
plt.gca().add_patch(shape)
plt.quiver(x, y, u, v, color='c', zorder = 1)
plt.axes().set_aspect('equal')
plt.show()

Tips:向量场存储在矩阵u和v中,我们从向量场中采样的每个向量的坐标;矩阵x和y表示样本位置。矩阵x、y、u和v被传递给pyplot.quiver(),即可呈现向量场。
系列链接
Python-Matplotlib可视化(1)——一文详解常见统计图的绘制
Python-Matplotlib可视化(2)——自定义颜色绘制精美统计图
Python-Matplotlib可视化(3)——自定义样式绘制精美统计图
Python-Matplotlib可视化(4)——添加注释让统计图通俗易懂
Python-Matplotlib可视化(5)——添加自定义形状绘制复杂图形
Python-Matplotlib可视化(6)——自定义坐标轴让统计图清晰易懂
Python-Matplotlib可视化(7)——多方面自定义统计图绘制
Python-Matplotlib可视化(8)——图形的输出与保存
Python-Matplotlib可视化(10)——一文详解3D统计图的绘制
