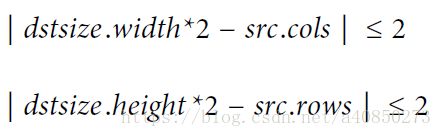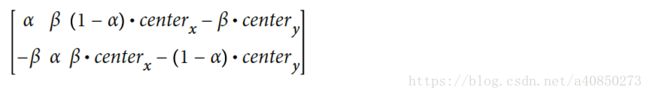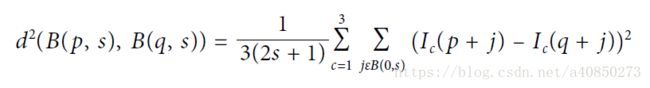Learning Opencv 3 —— 十一章 通用图像变换 General Image Transforms
Opencv 通用图像变换 General Image Transforms
相比于一类图像变换——卷积,其特点是图像中某个像素点的值只周围的几个像素点的值有关,而本文将介绍的图像变换并不属于此类。
拉伸、收缩、扭曲和旋转
Uniform Resize
void cv::resize(
cv::InputArray src, // Input image
cv::OutputArray dst, // Result image
cv::Size dsize, // New size
double fx = 0, // x-rescale
double fy = 0, // y-rescale
int interpolation = CV::INTER_LINEAR // interpolation method
);参数说明:
- src,dst:输入和输出图像
- dsize:输出图像的目标大小
- fx,fy:x 和 y 方向的缩放因子。这两个参数和 dsize 比有一个为零值
- 插值方法:可选参数如下
需要留意的是 cv::Mat::resize() 与该函数效果类似,但是并不进行内插和外推操作。
图像金字塔 Image Pyramids
cv::pyrDown() 首先使用高斯核对图像进行滤波,之后删除其中偶数行偶数列的。使得处理之后的图像变为原来大小的四分之一。
void cv::pyrDown(
cv::InputArray src, // Input image
cv::OutputArray dst, // Result image
const cv::Size& dstsize = cv::Size() // Output image size
);其中 dstsize 可以指定最后图像的大小,但是这个大小有个严格的限制。
其主要限制了最后的图像大小必须十分接近原图大小的一半。
cv::buildPyramid() 可以一次性产生一系列 cv::pyrDown() 的输出图像。
void cv::buildPyramid(
cv::InputArray src, // Input image
cv::OutputArrayOfArrays dst, // Output images from pyramid
int maxlevel // Number of pyramid levels
);其中 maxlevel 给出了金字塔的层数,必须大于等于 0。而最后的图像集将包含 maxlevel + 1,其中第一张图像将是原图。
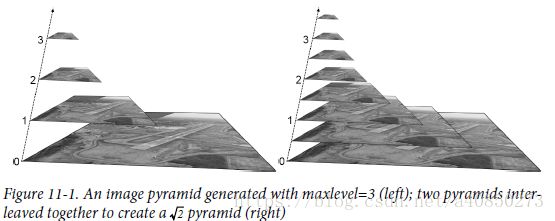
如果你需要一个指定比例的缩放金字塔,而不是固定的2,比如 ![]() , 一种可选的方式是通过 resize() 函数得到一个原图的
, 一种可选的方式是通过 resize() 函数得到一个原图的 ![]() 分之一的图像,再分别对原图和处理后的图像调用 cv::buildPyramid(),之后将结果进行组合得到最后的结果。
分之一的图像,再分别对原图和处理后的图像调用 cv::buildPyramid(),之后将结果进行组合得到最后的结果。
同理,cv::pyrUp() 转换原图为一个长宽均为两倍大的图像。这里,函数首先将长宽扩展一倍,并为偶数行赋值为 0,之后再使用高斯核得到丢失位置的像素值。
void cv::pyrUp(
cv::InputArray src, // Input image
cv::OutputArray dst, // Result image
const cv::Size& dstsize = cv::Size() // Output image size
);同理,dstsize 如果给出,必须满足如下限制。
从 上面的操作可以看出,cv::pyrUp() 并不是 cv::pyrDown() 的逆操作,因为在 cv::pyrDown() 时一部分图像的信息已经丢失。为此,Opencv 特别引入一个拉普拉斯金字塔,其第 i 层可通过下式进行计算。
基于拉普拉斯金字塔中的图像信息,我们就能完整的恢复出经过 cv::pyrDown() 处理之后的图像。
非均匀映射
非均匀映射可以实现拉伸,收缩,扭曲和旋转,其主要分为两类:仿射变换(变换矩阵为 2 * 3)和透视变换或者被称为齐次变换(变换矩阵为 3 * 3)的。
仿射变换可以把一个平行四边形映射为任意其他的平行四边形。当我们已知多张图片是同一物体在稍微改变一点视角的情况下拍摄的,仿射变换通常被用来求解不同视图之间的变换矩阵。因为其相比于齐次变换具有更少的估计参数更容易被求解。不过,由于这种情况并不完全属于仿射变换,而属于齐次变换,因此这种简化通常只在视图变换较小的情况下才适用。
透视变换是相机拍摄所符合的变换,其能够将矩形变为任意的四边形。
仿射变换
cv::warpAffine() 提供了对于图像的仿射变换,由于存在扭曲,因此其中也使用插值。
void cv::warpAffine(
cv::InputArray src, // Input image
cv::OutputArray dst, // Result image
cv::InputArray M, // 2-by-3 transform mtx
cv::Size dsize, // Destination image size
int flags = cv::INTER_LINEAR, // Interpolation, inverse
int borderMode = cv::BORDER_CONSTANT, // Pixel extrapolation
const cv::Scalar& borderValue = cv::Scalar() // For constant borders
);参数说明:
- src,dst:输入和输出图像
- M:期望的仿射变换矩阵,其中的前两列给出了仿射变换矩阵,最后一列的两个元素给定了 x 和 y 方向上的平移变量。具体计算公式如下。
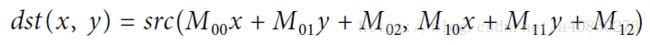
- flags:选择插值方法,见上表。同时,增加 cv::WARP_INVERSE_MAP 使得可以方便地实现逆变换
- borderMode,borderValue:给出了边界的填充方式
而 cv::getAffineTransform() 可以被用来求解映射矩阵 ![]() 。
。
cv::Mat cv::getAffineTransform( // Return 2-by-3 matrix
const cv::Point2f* src, // Coordinates *three* of vertices
const cv::Point2f* dst // Target coords, three vertices
);其中 src 和 dst 通常包含 3 个 2 维的点。
另一种计算 映射矩阵 ![]() 的方法是 cv::getRotationMatrix2D()。
的方法是 cv::getRotationMatrix2D()。
cv::Mat cv::getRotationMatrix2D( // Return 2-by-3 matrix
cv::Point2f center // Center of rotation
double angle, // Angle of rotation
double scale // Rescale after rotation
);其虽然不如 cv::getAffineTransform() 通用,但其给出了一种常用变换的方式:通过给定旋转点,旋转角度和缩放大小来进行仿射变换。如果假定 α = scale * cos(angle),β = scale * sin(angle) 可得仿射矩阵为
下面的例子综合了以上介绍的函数。
// Example 11-1. An affine transformation.
// Maps the 3 points (0, 0), (0, height-1), (width-1, 0) specified in srcTri[] to
// the specified points in array dstTri using a computed Affine Transform.
#include
#include
using namespace std;
int main(int argc, char** argv) {
if(argc != 2) {
cout << "Warp affine\nUsage: " <\n" << endl;
return -1;
}
cv::Mat src = cv::imread(argv[1],1);
if( src.empty() ) { cout << "Can not load " << argv[1] << endl; return -1; }
cv::Point2f srcTri[] = {
cv::Point2f(0,0), // src Top left
cv::Point2f(src.cols-1, 0), // src Top right
cv::Point2f(0, src.rows-1) // src Bottom left
};
cv::Point2f dstTri[] = {
cv::Point2f(src.cols*0.f, src.rows*0.33f), // dst Top left
cv::Point2f(src.cols*0.85f, src.rows*0.25f), // dst Top right
cv::Point2f(src.cols*0.15f, src.rows*0.7f) // dst Bottom left
};
// COMPUTE AFFINE MATRIX
//
cv::Mat warp_mat = cv::getAffineTransform(srcTri, dstTri);
cv::Mat dst, dst2;
cv::warpAffine(
src,
dst,
warp_mat,
src.size(),
cv::INTER_LINEAR,
cv::BORDER_CONSTANT,
cv::Scalar()
);
for( int i = 0; i < 3; ++i )
cv::circle(dst, dstTri[i], 5, cv::Scalar(255, 0, 255), -1, cv::LINE_AA);
cv::imshow("Affine Transform Test", dst);
cv::waitKey();
for(int frame=0;;++frame) {
// COMPUTE ROTATION MATRIX
cv::Point2f center(src.cols*0.5f, src.rows*0.5f);
double angle = frame*3 % 360, scale = (cos((angle - 60)* CV_PI/180) + 1.05)*0.8;
cv::Mat rot_mat = cv::getRotationMatrix2D(center, angle, scale);
cv::warpAffine(
src,
dst,
rot_mat,
src.size(),
cv::INTER_LINEAR,
cv::BORDER_CONSTANT,
cv::Scalar()
);
cv::imshow("Rotated Image", dst);
if(cv::waitKey(30) >= 0 )
break;
}
return 0;
}
cv::transform() 给出了对于点的仿射函数。
void cv::transform(
cv::InputArray src, // Input N-by-1 array (Ds channels)
cv::OutputArray dst, // Output N-by-1 array (Dd channels)
cv::InputArray mtx // Transform matrix (Ds-by-Dd)
);其中 N 为点数,而点的维数分别为 Ds 和 Dd。
cv::invertAffineTransform() 实现了逆仿射变换,其通过给定仿射矩阵,给出其逆仿射矩阵。
void cv::invertAffineTransform(
cv::InputArray M, // Input 2-by-3 matrix
cv::OutputArray iM // Output also a 2-by-3 matrix
);透视变换
首先必须注意的是透视变换虽然矩阵乘法实现,但由于其最后需要除以最后一维,因此其并不是一个线性变换。
cv::warpPerspective() 给出了透视变换函数
void cv::warpPerspective(
cv::InputArray src, // Input image
cv::OutputArray dst, // Result image
cv::InputArray M, // 3-by-3 transform mtx
cv::Size dsize, // Destination image size
int flags = cv::INTER_LINEAR, // Interpolation, inverse
int borderMode = cv::BORDER_CONSTANT, // Extrapolation method
const cv::Scalar& borderValue = cv::Scalar() // For constant borders
);其中目标图像的像素位置可按下式计算。
对比仿射变换的计算公式,可以得出矩阵第三行的前两列元素对应着透视变换部分,而 ![]() 通常通过变换保持为 1。这也再次印证了仿射变换时透视变换的一个特例。
通常通过变换保持为 1。这也再次印证了仿射变换时透视变换的一个特例。
cv::getPerspectiveTransform() 给出了计算透视变换矩阵的方法
cv::Mat cv::getPerspectiveTransform( // Return 3-by-3 matrix
const cv::Point2f* src, // Coordinates of *four* vertices
const cv::Point2f* dst // Target coords, four vertices
);其中 src 和 dst 都是四个点的向量。
下面的例子给出了透视变换的具体使用方式
// Example 11-2. Code for perspective transformation
// Compute a perspective transformation between the 4 src control points
// in srcQuad to 4 dst control points in dstQuad and apply it the image.
#include
#include
using namespace std;
int main(int argc, char** argv) {
if(argc != 2) {
cout << "Perspective Warp\nUsage: " <\n" << endl;
return -1;
}
cv::Mat src = cv::imread(argv[1],1);
if( src.empty() ) { cout << "Can not load " << argv[1] << endl; return -1; }
cv::Point2f srcQuad[] = {
cv::Point2f(0, 0), // src Top left
cv::Point2f(src.cols-1, 0), // src Top right
cv::Point2f(src.cols-1, src.rows-1), // src Bottom right
cv::Point2f(0, src.rows-1) // src Bottom left
};
cv::Point2f dstQuad[] = {
cv::Point2f(src.cols*0.05f, src.rows*0.33f),
cv::Point2f(src.cols*0.9f, src.rows*0.25f),
cv::Point2f(src.cols*0.8f, src.rows*0.9f),
cv::Point2f(src.cols*0.2f, src.rows*0.7f)
};
// COMPUTE PERSPECTIVE MATRIX
//
cv::Mat warp_mat = cv::getPerspectiveTransform(srcQuad, dstQuad);
cv::Mat dst;
cv::warpPerspective(src, dst, warp_mat, src.size(), cv::INTER_LINEAR,
cv::BORDER_CONSTANT, cv::Scalar());
for( int i = 0; i < 4; i++ )
cv::circle(dst, dstQuad[i], 5, cv::Scalar(255, 0, 255), -1, cv::LINE_AA);
cv::imshow("Perspective Transform Test", dst);
cv::waitKey();
return 0;
}
cv::perspectiveTransform() 实现了对点的透视变换
void cv::perspectiveTransform(
cv::InputArray src, // Input N-by-1 array (2 or 3 channels)
cv::OutputArray dst, // Output N-by-1 array (2 or 3 channels)
cv::InputArray mtx // Transform matrix (3-by-3 or 4-by-4)
);
这里由于透视变换是将在三维空间中的一个平面向另一个不同的二维子空间进行投影,因此如果图片是 2 维的,那么透视变换矩阵就应该是 3 维的;而如果图片是 3 维的,那么透视变换矩阵就应该是 4 维的。具体介绍可以参考:Opencv 摄像机模型与标定 Camera Models and Calibration
极坐标映射
cv::cartToPolar() 实现从直角坐标系向极坐标系之间的转变。
void cv::cartToPolar(
cv::InputArray x, // Input single channel x-array
cv::InputArray y, // Input single channel y-array
cv::OutputArray magnitude, // Output single channel mag-array
cv::OutputArray angle, // Output single channel angle-array
bool angleInDegrees = false // Set true for degrees, else radians
);如果 angleInDegrees 为真,angle 将以度给出;否则将以弧度给出。
这里有一个实用的例子,可能用到这个函数。当你通过 cv::Sobel() 或 cv::DFT() 或 cv::filter2D() 获得图像 x 和 y 方向的微分之后,可以使用 cartToPolar() 得到梯度的幅度和方向,从而根据幅度阈值筛选像素点,并给出梯度的方向。
相应的 cv::polarToCart() 实现从极坐标系向直角坐标系之间的转变。
void cv::polarToCart(
cv::InputArray magnitude, // Output single channel mag-array
cv::InputArray angle, // Output single channel angle-array
cv::OutputArray x, // Input single channel x-array
cv::OutputArray y, // Input single channel y-array
bool angleInDegrees = false // Set true for degrees, else radians
);对数极坐标系
对数极坐标系基于某个点 ![]() 按
按 ![]() ,
,![]() 进行变换.
进行变换.
void cv::logPolar(
cv::InputArray src, // Input image
cv::OutputArray dst, // Output image
cv::Point2f center, // Center of transform
double m, // Scale factor
int flags = cv::INTER_LINEAR // interpolation and fill modes
| cv::WARP_FILL_OUTLIERS
);进行如此变换的主要原因是在固定中心点的情况,旋转和缩放的图像在变换到对数极坐标系下之后只表现为缩放和平移。
// Example 11-3. Log-polar transform example
// Log-polar transform example.
// This demonstrates the forward and backward (inverse) log-polar
// transform.
#include
#include
using namespace std;
int main(int argc, char** argv) {
if(argc != 3) {
cout << "LogPolar\nUsage: " < \n"
<<"~30 is usually good enough\n";
return -1;
}
cv::Mat src = cv::imread(argv[1],1);
if( src.empty() ) { cout << "Can not load " << argv[1] << endl; return -1; }
double M = atof(argv[2]);
cv::Mat dst(src.size(), src.type()), src2(src.size(), src.type());
cv::logPolar(
src,
dst,
cv::Point2f(src.cols*0.5f, src.rows*0.5f),
M,
cv::INTER_LINEAR | cv::WARP_FILL_OUTLIERS
);
cv::logPolar(
dst,
src2,
cv::Point2f(src.cols*0.5f, src.rows*0.5f),
M,
cv::INTER_LINEAR | cv::WARP_INVERSE_MAP
);
cv::imshow( "log-polar", dst );
cv::imshow( "inverse log-polar", src2 );
cv::waitKey();
return 0;
}
任意映射
void cv::remap(
cv::InputArray src, // Input image
cv::OutputArray dst, // Output image
cv::InputArray map1, // target x for src pix
cv::InputArray map2, // target y for src pix
int interpolation = cv::INTER_LINEAR, // Interpolation, inverse
int borderMode = cv::BORDER_CONSTANT, // Extrapolation method
const cv::Scalar& borderValue = cv::Scalar() // For constant borders
);该函数通过用户指定 x 和 y 方向上的映射函数,实现任意映射的功能。
图像修复
cv::inpaint() 可以实现图像的修复,但是图像中的修复位置不能太厚,即损坏部分周围必须包含足够的原始图片的纹理和色彩信息。
void cv::inpaint(
cv::InputArray src, // Input image: 8-bit, 1 or 3 channels
cv::InputArray inpaintMask, // 8-bit, 1 channel. Inpaint nonzeros
cv::OutputArray dst, // Result image
double inpaintRadius, // Range to consider around pixel
int flags // Select NS or TELEA
);参数说明:
- src:包含损坏点的原始图像
- inpaintMask:非零点标示了原始图像中破坏的位置
- dst:修补后的图像
- inpaintRadius:指定了使用周围多大范围内的像素来进行修补。同时,设置一个较小的,比如 3,否则将造成很明显的平滑的痕迹
- flags:修补方法的选择,这里只给出两种方法——cv::INPAINT_NS (Navier-Stokes method) 和 cv::INPAINT_TELEA (A. Telea’s method)
去噪
在大多数场景下,噪声通常是由于低光照条件下,数字图像的增益必须加大,这也就造成噪声也被放大。Opencv 中实现的降噪算法被称为 Fast Non-Local Means Denoising (FNLMD),其基本原理是寻找周围的相似像素,然后平均。这里的相似不是基于相似的色彩或者强度,而是基于相似的环境。其通过下式来计算两块区域的相似性
并通过下式来计算对应区域加权的权重
void cv::fastNlMeansDenoising(
cv::InputArray src, // Input image
cv::OutputArray dst, // Output image
float h = 3, // Weight decay parameter
int templateWindowSize = 7, // Size of patches used for comparison
int searchWindowSize = 21 // Maximum patch distance to consider
);其中 templateWindowSize 就是多大的窗口被用于比较,而 searchWindowSize 就是最远多远的窗口将参与加权。
下面这张表给出了以下可供参考的参数值
void cv::fastNlMeansDenoisingColored(
cv::InputArray src, // Input image
cv::OutputArray dst, // Output image
float h = 3, // Luminosity weight decay parameter
float hColor = 3, // Color weight decay parameter
int templateWindowSize = 7, // Size of patches used for comparison
int searchWindowSize = 21 // Maximum patch distance to consider
);该算法首先将 RGB 图像转换到 LAB 颜色空间,使用 FNLMD 去除噪声之后,再将图像变换 RGB 空间。转换到 LAB 的原因是对于亮度可以设置一个不同的延迟参数。
void cv::fastNlMeansDenoisingMulti(
cv::InputArrayOfArrays srcImgs, // Sequence of several images
cv::OutputArray dst, // Output image
int imgToDenoiseIndex, // Index of image to denoise
int temporalWindowSize, // Num images to use (odd)
float h = 3, // Weight decay parameter
int templateWindowSize = 7, // Size of comparison patches
int searchWindowSize = 21 // Maximum patch distance
);
void cv::fastNlMeansDenoisingColoredMulti(
cv::InputArrayOfArrays srcImgs, // Sequence of several images
cv::OutputArray dst, // Output image
int imgToDenoiseIndex, // Index of image to denoise
int temporalWindowSize, // Num images to use (odd)
float h = 3, // Weight decay param
float hColor = 3, // Weight decay param for color
int templateWindowSize = 7, // Size of comparison patches
int searchWindowSize = 21 // Maximum patch distance
);这两个函数作用于序列图片,使用多帧图片来辅助进行去噪操作。其中 imgToDenoiseIndex 指定了需要去噪的图片;temporalWindowSize 指定了使用前后多少帧图片参与去噪,必须为奇数。
直方图均衡化
在标准的照相机中,通过设置快门和光圈的大小来控制获得不多也不少的曝光。然而对于每张照片对比度的范围通常大于相机的动态范围。因此必须在获取阴影部分的细节与避免图像饱和白花之间进行权衡。虽然一张照片在拍摄之后我们无法改变所记录的内容,但是仍然可以通过直方图均衡化来增加照片的对比度。
void cv::equalizeHist(
const cv::InputArray src, // Input image
cv::OutputArray dst // Result image
);此函数只能处理单通道图像,即灰度图像。对于彩色图像,你可以对通道进行拆分之后分别处理,但这通常不能获得满意的效果。建议的做法是将 RGB 图像转换到 LAB 空间中,并只对亮度通道进行直方图均衡化操作。