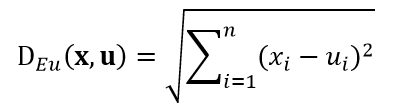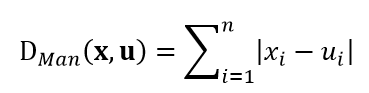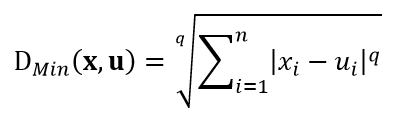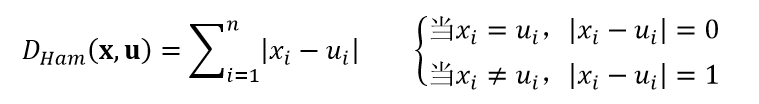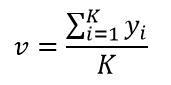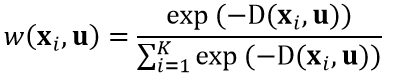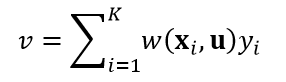Opencv2.4.9源码分析——K-Nearest Neighbors
一、原理
K近邻算法(KNN,K-NearestNeighbors)是一种非常简单的机器学习方法,它既可以处理分类问题,也可以处理回归问题,而且它的执行效果非常好。
KNN是一种懒惰学习算法(lazy learningalgorithm)。所谓懒惰算法指的是,直到有了新的测试样本,该算法才开始依据训练样本进行样本的预测处理工作,也就是说该算法事先不会对训练样本进行任何的处理,只会“懒散”的等待测试样本的到来,然后才开始工作。与懒惰学习算法相对应的是渴望学习算法(eager learning algorithm),它会在测试之前利用训练样本建立一个统一的、与输入量相独立的目标函数,测试样本就是利用该函数进行预测,因此一旦目标函数创建完成,训练样本数据就可以完全抛弃掉。与渴望学习算法相比,懒惰学习算法所构建的目标函数能够更近似测试样本数据本身,但同时它需要更大的存储空间用于存储训练样本数据。总之,懒惰学习算法非常适用于那些需要处理具有较少特征属性的大型数据库的问题。
下面我们给出KNN算法的原理。
在训练样本集中,每个样本都是一个具有n个特征属性的向量,即x = (x1,x2,…,xn),因此可以认为每个样本在n维特征空间,或度量空间内分布。每个样本还有一个唯一属于它的标签y,机器学习的目的就是找到这样的一个函数f,使y=f(x),这样当有一个新的样本u时,我们就可以通过该目标函数确定它的标签。
既然样本可以被认为是在度量空间内分布,那么我们就可以用距离测度来衡量它们的相似程度。常用的距离测度包括欧氏距离和曼哈顿距离,以及更一般的明氏距离,式1~式3分别给出了测试样本u和训练样本x的这三种距离公式:
上述三个距离测度只适用于特征属性是连续变量的情况,当特征属性是离散变量时,如对文本进行分类,我们就需要用汉明距离:
KNN的任务就是在训练样本集中,依据距离测度找到与测试样本u最相似的那K个训练样本x。对于分类问题,我们采用“多数表决”的方式来确定u的最终分类,即这K个训练样本中,哪个分类的样本数多,u就属于哪个分类。而对于回归问题,u的预测值v为:
对于KNN来说,有一个最重要的参数需要事先确定,那就是K值。选择不同的K值,最终的预测结果可能会不同。K值选取的过小,会引入误差,而K值过大,虽然更准确,但会使在特征空间内明确的边界变得模糊。因此K值既要足够的大,以保证预测结果的正确性,又要足够的小,以使K个训练样本与测试样本具有一定的相似性。目前选择K值比较常用的方法是交叉验证方法(cross-validation)。
另一个需要讨论的问题是,在前面的计算中,我们认为这K个与测试样本距离最相似的训练样本对测试样本具有相同的影响,也就是我们并没有考虑训练样本与测试样本之间距离大小的影响。对于这个问题,我们可以使用距离权值来解决,即让距离更小的样本具有更大的权值。K个最邻近样本中第i个样本xi与测试样本u的权值可以定义为:
式中,D(xi,u)表示式1~式4中的任一距离。对于回归问题,最终的预测结果v为:
而对于分类问题,最终的分类结果为权值最大的那个类。
需要说明的是,OpenCV并没有采用交叉验证和距离权值的方法。
二、源码分析
CvKNearest类的两个构造函数:
CvKNearest::CvKNearest()
{
samples = 0; //表示训练样本数据
clear(); //主要是清空变量samples
}
CvKNearest::CvKNearest( const CvMat* _train_data, const CvMat* _responses,
const CvMat* _sample_idx, bool _is_regression, int _max_k )
{
samples = 0;
train( _train_data, _responses, _sample_idx, _is_regression, _max_k, false );
}
其中,_train_data表示训练样本数据,_responses表示训练样本数据的响应值,_sample_idx表示训练样本数据的索引,即只使用该索引所指定的那些样本,_is_regression表示KNN的类型,即是分类问题还是回归问题,默认为false,是分类问题,_max_k表示近邻的最大数量,默认为32。
KNN算法的训练函数train。因为KNN是懒惰学习算法,因此该函数的作用是初始化训练样本数据,为真正的测试样本做准备。
bool CvKNearest::train( const CvMat* _train_data, const CvMat* _responses,
const CvMat* _sample_idx, bool _is_regression,
int _max_k, bool _update_base )
//_update_base表示该KNN模型是不是仅仅需要更新样本数据,_update_base为true表示使用新的样本数据更新原有的KNN模型,_update_base为false(默认)表示应用该样本数据构建新的KNN模型
{
bool ok = false; //该函数返回标识变量,表示是否训练成功
CvMat* responses = 0; //表示样本响应值
CV_FUNCNAME( "CvKNearest::train" );
__BEGIN__;
CvVectors* _samples = 0;
float** _data = 0; //表示完整的样本数据
//_count表示训练样本的数量,_dims和_dims_all都表示特征属性的数量,_rsize表示样本响应值的大小
int _count = 0, _dims = 0, _dims_all = 0, _rsize = 0;
if( !_update_base ) //重新构建KNN模型,则清空原有样本数据samples
clear();
// Prepare training data and related parameters.
// Treat categorical responses as ordered - to prevent class label compression and
// to enable entering new classes in the updates
//调用cvPrepareTrainData函数,为KNN算法准备样本数据,即初始化样本。首先检查样本_train_data,该变量矩阵一定要是CV_ROW_SAMPLE,即矩阵的行表示样本,列表示特征属性,并且不能有缺失的属性;然后根据_sample_idx确定那些真正要用到的样本数据;再确定样本的响应值,它必须为CV_VAR_ORDERED;最终得到完整的样本数据_data。
CV_CALL( cvPrepareTrainData( "CvKNearest::train", _train_data, CV_ROW_SAMPLE,
_responses, CV_VAR_ORDERED, 0, _sample_idx, true, (const float***)&_data,
&_count, &_dims, &_dims_all, &responses, 0, 0 ));
//确保变量responses正确
if( !responses )
CV_ERROR( CV_StsNoMem, "Could not allocate memory for responses" );
//确保应用所有的特征属性
if( _update_base && _dims != var_count )
CV_ERROR( CV_StsBadArg, "The newly added data have different dimensionality" );
if( !_update_base ) //如果是重新构建KNN模型
{
if( _max_k < 1 ) //确保参数_max_k必须是正数
CV_ERROR( CV_StsOutOfRange, "max_k must be a positive number" );
//赋值
regression = _is_regression;
var_count = _dims;
max_k = _max_k;
}
_rsize = _count*sizeof(float); //定义样本响应值的大小,
CV_CALL( _samples = (CvVectors*)cvAlloc( sizeof(*_samples) + _rsize )); //分配空间
//为样本数据赋值
_samples->next = samples;
_samples->type = CV_32F;
_samples->data.fl = _data;
_samples->count = _count;
total += _count;
samples = _samples;
//复制样本响应值responses
memcpy( _samples + 1, responses->data.fl, _rsize );
ok = true;
__END__;
if( responses && responses->data.ptr != _responses->data.ptr )
cvReleaseMat(&responses);
return ok;
}
实现KNN算法的find_nearest函数:
float CvKNearest::find_nearest( const CvMat* _samples, int k, CvMat* _results,
const float** _neighbors, CvMat* _neighbor_responses, CvMat* _dist ) const
//_samples表示待测试的样本数据,该变量必须是矩阵形式,行表示样本,列表示特征属性,数据类型为CV_32FC1,而且该样本的特征属性的数量必须与训练样本的特征属性的数量一致
//k表示KNN算法的参数K,它的值应该在1和max_k之间
//_results表示测试样本的预测结果,为向量的形式,向量中元素的数量必须为测试样本的数量,即如果是一次预测多个样本,则预测结果用该变量表示。如果是分类问题,数据类型为CV_32SC1,如果是回归问题,则为CV_32FC1
//_neighbors表示返回测试样本的k个最邻近的训练样本
//_neighbor_responses表示返回测试样本的k个最邻近训练样本的响应值,该参数为矩阵形式,数据类型为CV_32FC1,矩阵的行表示测试样本,矩阵的列表示k个响应值
//_dist表示返回测试样本的k个最邻近训练样本与测试样本的距离,该参数为矩阵形式,数据类型为CV_32FC1,矩阵的行表示测试样本,矩阵的列表示k个距离
{
//该变量为该函数的返回值,它表示如果只有一个测试样本,则该函数就用该变量返回预测结果
float result = 0.f;
//用于开辟一块内存空间的最大常数
const int max_blk_count = 128, max_buf_sz = 1 << 12;
//确保训练样本数据已准备好
if( !samples )
CV_Error( CV_StsError, "The search tree must be constructed first using train method" );
//确保参数_samples的正确性
if( !CV_IS_MAT(_samples) ||
CV_MAT_TYPE(_samples->type) != CV_32FC1 ||
_samples->cols != var_count )
CV_Error( CV_StsBadArg, "Input samples must be floating-point matrix (x)" );
//确保参数_results的正确性
if( _results && (!CV_IS_MAT(_results) ||
(_results->cols != 1 && _results->rows != 1) ||
_results->cols + _results->rows - 1 != _samples->rows) )
CV_Error( CV_StsBadArg,
"The results must be 1d vector containing as much elements as the number of samples" );
//确保参数_results的数据类型的正确性
if( _results && CV_MAT_TYPE(_results->type) != CV_32FC1 &&
(CV_MAT_TYPE(_results->type) != CV_32SC1 || regression))
CV_Error( CV_StsUnsupportedFormat,
"The results must be floating-point or integer (in case of classification) vector" );
//确保参数k在正确区间范围内
if( k < 1 || k > max_k )
CV_Error( CV_StsOutOfRange, "k must be within 1..max_k range" );
//确保参数_neighbor_responses的正确性
if( _neighbor_responses )
{
if( !CV_IS_MAT(_neighbor_responses) || CV_MAT_TYPE(_neighbor_responses->type) != CV_32FC1 ||
_neighbor_responses->rows != _samples->rows || _neighbor_responses->cols != k )
CV_Error( CV_StsBadArg,
"The neighbor responses (if present) must be floating-point matrix of x size" );
}
//确保参数_dist的正确性
if( _dist )
{
if( !CV_IS_MAT(_dist) || CV_MAT_TYPE(_dist->type) != CV_32FC1 ||
_dist->rows != _samples->rows || _dist->cols != k )
CV_Error( CV_StsBadArg,
"The distances from the neighbors (if present) must be floating-point matrix of x size" );
}
int count = _samples->rows; //表示测试样本的数量
int count_scale = k*2;
int blk_count0 = MIN( count, max_blk_count );
int buf_sz = MIN( blk_count0 * count_scale, max_buf_sz );
blk_count0 = MAX( buf_sz/count_scale, 1 );
blk_count0 += blk_count0 % 2;
blk_count0 = MIN( blk_count0, count );
buf_sz = blk_count0 * count_scale + k; //表示开辟内存空间的大小
int k1 = get_sample_count(); //得到训练样本的数量
//选取k1和k的最小值,一般来说,最终的k1就等于KNN中的参数k
k1 = MIN( k1, k );
//调用P1函数,并行处理每个测试样本,该语句需要TBB库支持
cv::parallel_for_(cv::Range(0, count), P1(this, buf_sz, k, _samples, _neighbors, k1,
_results, _neighbor_responses, _dist, &result)
);
return result;
}
struct P1 : cv::ParallelLoopBody {
P1(const CvKNearest* _pointer, int _buf_sz, int _k, const CvMat* __samples, const float** __neighbors,
int _k1, CvMat* __results, CvMat* __neighbor_responses, CvMat* __dist, float* _result)
{
pointer = _pointer;
k = _k;
_samples = __samples;
_neighbors = __neighbors;
k1 = _k1;
_results = __results;
_neighbor_responses = __neighbor_responses;
_dist = __dist;
result = _result;
buf_sz = _buf_sz;
}
const CvKNearest* pointer;
int k;
const CvMat* _samples;
const float** _neighbors;
int k1;
CvMat* _results;
CvMat* _neighbor_responses;
CvMat* _dist;
float* result;
int buf_sz;
//重载()运算符
void operator()( const cv::Range& range ) const
{
cv::AutoBuffer buf(buf_sz); //定义一块内存空间
for(int i = range.start; i < range.end; i += 1 ) //遍历所有测试样本
{
float* neighbor_responses = &buf[0]; //定义neighbor_responses所用空间
float* dist = neighbor_responses + 1*k; //定义dist所用空间
Cv32suf* sort_buf = (Cv32suf*)(dist + 1*k); //定义sort_buf所用空间
//调用find_neighbors_direct函数,得到k个最邻近的训练样本_neighbors、训练样本响应值neighbor_responses、以及距离dist
pointer->find_neighbors_direct( _samples, k, i, i + 1,
neighbor_responses, _neighbors, dist );
//调用write_results函数,得到最终的测试样本的响应值,即预测结果,该函数的返回值为只有一个测试样本时的响应值,如果是多个测试样本,则响应值为_results
float r = pointer->write_results( k, k1, i, i + 1, neighbor_responses, dist,
_results, _neighbor_responses, _dist, sort_buf );
if( i == 0 ) //如果只有一个测试样本,则赋值该样本的响应值
*result = r;
}
}
};
void CvKNearest::find_neighbors_direct( const CvMat* _samples, int k, int start, int end,
float* neighbor_responses, const float** neighbors, float* dist ) const
{
//count表示测试样本的数量,其实该值为1,d表示特征属性的数量
int i, j, count = end - start, k1 = 0, k2 = 0, d = var_count;
CvVectors* s = samples; //表示训练样本
//遍历所有集合的训练样本,在前面训练样本时,不同时期得到的训练样本是放到不同的集合中的
for( ; s != 0; s = s->next )
{
int n = s->count; //表示该集合内的训练样本的数量
for( j = 0; j < n; j++ ) //遍历该集合内的所有训练样本
{
for( i = 0; i < count; i++ ) //遍历测试样本
{
// sum表示距离,即式1的结果,这里为了减小误差,并没有对距离进行开方运算,也就是只计算了根号内的值
double sum = 0;
Cv32suf si;
const float* v = s->data.fl[j]; //得到当前训练样本
//得到当前测试样本
const float* u = (float*)(_samples->data.ptr + _samples->step*(start + i));
//dd表示当前测试样本与k个最邻近的训练样本的距离,该dd数组是按照由小到大的距离顺序排列的,即dd[0]距离最小,dd[k-1]最大
Cv32suf* dd = (Cv32suf*)(dist + i*k);
float* nr;
const float** nn;
int t, ii, ii1;
//应用式1,计算距离,在这里为了加快运算速度,按照每4个特征属性为一组进行一次for循环计算,不够4个的则应用下一个for循环
for( t = 0; t <= d - 4; t += 4 )
{
double t0 = u[t] - v[t], t1 = u[t+1] - v[t+1];
double t2 = u[t+2] - v[t+2], t3 = u[t+3] - v[t+3];
sum += t0*t0 + t1*t1 + t2*t2 + t3*t3;
}
for( ; t < d; t++ )
{
double t0 = u[t] - v[t];
sum += t0*t0;
}
si.f = (float)sum; //赋值
//对数组dd由后往前依次与当前计算的距离(sum)比较,由于dd的存储顺序是从小到大的顺序,因此当满足si.i > dd[ii].i时,此时的索引ii所对应的距离正好是小于si.i的最大的值
for( ii = k1-1; ii >= 0; ii-- )
if( si.i > dd[ii].i )
break;
//当ii >= k-1时,说明数组dd中已有k个距离值,并且当前计算的距离sum都大于这k个距离值,所以对此次计算的距离不做任何处理,直接舍弃
if( ii >= k-1 )
continue;
//nr表示测试样本的k个最邻近训练样本的响应值
nr = neighbor_responses + i*k;
//nn表示测试样本的k个最邻近的训练样本
nn = neighbors ? neighbors + (start + i)*k : 0;
//dd、nr和nn分别对应于参数_dist、_neighbor_responses和_neighbors,它们的排列顺序都是一致的,完全是按照测试样本的k个最邻近训练样本的距离值,从小到大的顺序排列的
//把索引ii以后的数组dd、nr和nn的值依次向后移一位
for( ii1 = k2 - 1; ii1 > ii; ii1-- )
{
dd[ii1+1].i = dd[ii1].i;
nr[ii1+1] = nr[ii1];
if( nn ) nn[ii1+1] = nn[ii1];
}
//把当前计算的距离si.i放到数组dd中的第ii+1的位置上,则数组dd仍然是按照从小到大的顺序排列的
dd[ii+1].i = si.i;
//把当前距离所对应的训练样本的响应值放到数组nr中的第ii+1的位置上,与数组dd中的元素相对应
nr[ii+1] = ((float*)(s + 1))[j];
//把当前距离所对应的训练样本放到数组nn中的第ii+1的位置上,与数组dd中的元素相对应
if( nn )
nn[ii+1] = v;
}
//同时逐一更新k1和k2值,即k1等于k2,直至k1大于k时,则k1始终为k,k2始终为k-1
k1 = MIN( k1+1, k );
k2 = MIN( k1, k-1 );
}
}
}
float CvKNearest::write_results( int k, int k1, int start, int end,
const float* neighbor_responses, const float* dist,
CvMat* _results, CvMat* _neighbor_responses,
CvMat* _dist, Cv32suf* sort_buf ) const
{
float result = 0.f;
//count表示测试样本的数量,其实该值为1
int i, j, j1, count = end - start;
// inv_scale表示k的倒数,即式5的分母部分
double inv_scale = 1./k1;
int rstep = _results && !CV_IS_MAT_CONT(_results->type) ? _results->step/sizeof(result) : 1;
//遍历测试样本
for( i = 0; i < count; i++ )
{
//得到当前测试样本的k个最邻近训练样本的响应值
const Cv32suf* nr = (const Cv32suf*)(neighbor_responses + i*k);
float* dst;
float r;
//_results有值表示有多个测试样本,start+i为0表示只有一个测试样本
if( _results || start+i == 0 )
{
if( regression ) //回归问题
{
double s = 0;
//得到k个最邻近训练样本的响应值之和,即式5的分子部分
for( j = 0; j < k1; j++ )
s += nr[j].f;
//式5
r = (float)(s*inv_scale);
}
else //分类问题
{
int prev_start = 0, best_count = 0, cur_count;
Cv32suf best_val;
//k个最邻近训练样本的响应值重新赋值给数组sort_buf
for( j = 0; j < k1; j++ )
sort_buf[j].i = nr[j].i;
//对这k个响应值按照由小到大的顺序进行排序
for( j = k1-1; j > 0; j-- )
{
bool swap_fl = false;
for( j1 = 0; j1 < j; j1++ )
if( sort_buf[j1].i > sort_buf[j1+1].i )
{
int t;
CV_SWAP( sort_buf[j1].i, sort_buf[j1+1].i, t );
swap_fl = true;
}
if( !swap_fl )
break;
}
best_val.i = 0; //表示表决结果,即最佳响应值
//按照“多数表决”的原则,选择相同的响应值的数量最多的那个响应值
//遍历所有k个样本
for( j = 1; j <= k1; j++ )
// j == k1说明表决结束,应该要给出一个结果来;sort_buf[j].i != sort_buf[j-1].i说明相邻的两个样本的响应值不相同,这时就需要统计与前一个响应值相同的样本数量
if( j == k1 || sort_buf[j].i != sort_buf[j-1].i )
{
//得到与前一个响应值相同的样本数量
cur_count = j - prev_start;
//比较当前得到样本数量cur_count和以前得到的相同响应值最多的样本数量best_count,如果当前的样本数量多,则更新best_count
if( best_count < cur_count )
{
best_count = cur_count; //更新best_count
best_val.i = sort_buf[j-1].i; //得到表决结果
}
prev_start = j; //更新prev_start,即计数值的起始索引
}
r = best_val.f; //得到最终的表决结果
}
if( start+i == 0 ) //只有一个测试样本
result = r; //赋值
if( _results ) //有不止一个的测试样本,则响应值依次放入_results中
_results->data.fl[(start + i)*rstep] = r;
}
//把k个最邻近的训练样本的响应值放入dst中
if( _neighbor_responses )
{
dst = (float*)(_neighbor_responses->data.ptr +
(start + i)*_neighbor_responses->step);
for( j = 0; j < k1; j++ )
dst[j] = nr[j].f;
for( ; j < k; j++ )
dst[j] = 0.f;
}
//把k个最邻近的训练样本与测试样本的距离放入dst中
if( _dist )
{
dst = (float*)(_dist->data.ptr + (start + i)*_dist->step);
for( j = 0; j < k1; j++ )
dst[j] = dist[j + i*k];
for( ; j < k; j++ )
dst[j] = 0.f;
}
}
return result; //返回只有一个测试样本时的响应值
}
三、应用实例
下面我们就给出一个具体的应用实例。
有两种指标可以用于评价纸巾的好坏:耐酸性和强度。下面给出一组调查数据:
| 耐酸性(单位:秒) |
强度(单位:公斤/每平方米) |
分类(好:G;差:B) |
| 4 |
3 |
B |
| 1 |
3 |
B |
| 3 |
3 |
B |
| 3 |
7 |
B |
| 3 |
4 |
B |
| 4 |
1 |
B |
| 1 |
4 |
B |
| 5 |
6 |
B |
| 3 |
7 |
B |
| 6 |
2 |
B |
| 4 |
6 |
G |
| 4 |
4 |
G |
| 5 |
8 |
G |
| 7 |
8 |
G |
| 7 |
7 |
G |
| 10 |
5 |
G |
| 7 |
6 |
G |
| 4 |
10 |
G |
| 9 |
7 |
G |
| 5 |
4 |
G |
| 8 |
5 |
G |
| 6 |
6 |
G |
| 7 |
4 |
G |
| 8 |
8 |
G |
则我们预测某一样本,它的耐酸性和强度分别为4和5,具体程序如下所示:
#include "opencv2/core/core.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/ml/ml.hpp"
#include
using namespace cv;
using namespace std;
int main( int argc, char** argv )
{
float trainingData[24][2]={ {4, 3},{1, 3},{3, 3},{3, 7},
{3, 4},{4, 1},{1, 4},{5, 6},
{3, 7},{6, 2},{4, 6},{4, 4},
{5, 8},{7, 8},{7, 7},{10, 5},
{7, 6},{4, 10},{9, 7},{5, 4},
{8, 5},{6, 6},{7, 4},{8, 8} };
CvMat trainingDataCvMat = cvMat( 24, 2, CV_32FC1, trainingData );
float responses[24] = {'B','B','B','B','B','B','B','B','B','B',
'G','G','G','G','G','G','G','G','G','G','G','G','G','G'};
CvMat responsesCvMat = cvMat( 24, 1, CV_32FC1, responses );
//参数false表示分类问题
CvKNearest knn( &trainingDataCvMat, &responsesCvMat, 0, false, 32 );
int K = 7; //KNN算法的参数K值
float myData[2] = {4, 5};
CvMat myDataCvMat = cvMat(1, 2, CV_32FC1, myData);
//nearests表示K个最邻近样本的响应值
CvMat* nearests = cvCreateMat( 1, K, CV_32FC1);
float r = knn.find_nearest(&myDataCvMat, K, 0, 0, nearests, 0);
cout<<"result: "<<(char)r<data.fl[i];
return 0;
}
最终的结果为:
result: G
7 nearest responses: G G G B B B G