基于R语言的方差分析

1、导入相关的包

单因素方差分析

一、正态性检验

with(ToothGrowth, tapply(len, dosef, shapiro.test))

二、方差齐性检验

三组以上的因子需要用leveneTest()检验

leveneTest(len~dosef, ToothGrowth)

不过有一些教材认为应该用残差来检验正态性和方差齐性
因此这里需要进行一次方差分析

AOV1 <- aov(len~dosef, ToothGrowth)
summary(AOV1)

这里面的Residuals就是残差的意思，所以要将这数据提取处理，也可以在AOV1数据上面索引

三、诊断模型

res1 <- residuals(AOV1) 或者 res1 <- AOV1$residuals
shapiro.test(res1)
ggqqplot(res1) 画出qq图看以下

科普：
QQPlot图是用于直观验证一组数据是否来自某个分布，或者验证某两组数据是否来自同一（族）分布。在教学和软件中常用的是检验数据是否来自于正态分布。

方差齐性的检验和前面的差不多就是因变量变成了残差

leveneTest(res1~dosef, ToothGrowth)

然后进行进一步的分析，对于多组因子进行事后两两分析
TukeyHSD(AOV1)
得到各组两两比较的结果，均值之差，95%置信区间的上下界，以及校正后的P值

但是这个不是很明显，所以换另外一种写法

在后面加上
P<- Tu$dosef[,4]
format(P, scientific = F)

这样就能很好的看出p值的大小了

四、作图

最后我们要根据我们的数据进行作图
ggboxpot(ToothGrowth, x = ‘dosef’, y = ‘len’, fill = ‘dosef’, palette = ‘npg’) + stat_compare_means(method = ‘anova’)

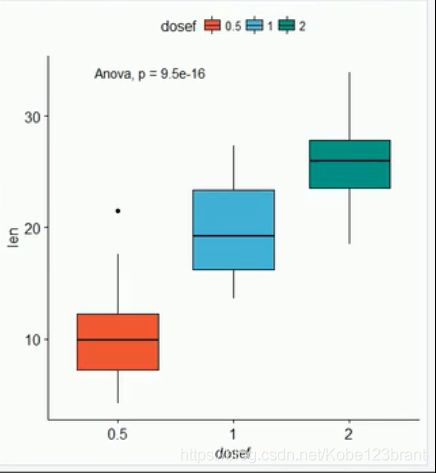
接下来使用ggplot包的本尊做法来画图
ggplot(ToothGrowth, x = dosef, y = len, fill = dosef) +
geom_boxplot()

在上面的基础上标出点的位置
ggplot(ToothGrowth, x = dosef, y = len, fill = dosef) +
geom_boxplot() +
geom_point()

在这个基础上，需要加入误差线，这是一般箱线图的画法
ggplot(ToothGrowth, x = dosef, y = len, fill = dosef) +
geom_boxplot(geom = ‘errorbar’) +
geom_boxplot() +
geom_point() +

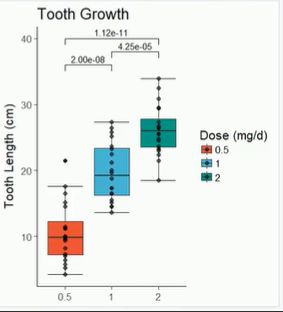
这里我将这三个组的两两比较结果画出来


这里就包含了两中表示显著性的方法，可以按照数字的形式表现出来，也可以用***表现出来

我们通常是需要将相同的图形成同一种分格，所以这里将风格保存为一个对象，方便后面的数据调用

如果符合正态分布，但是不假定方差齐性，需要用下面的方法检验（Welch ANOVA）

oneway.test(len~dosef, ToothGrowth, var.equal = F) 这里的参数如果设置为True，就是经典的ANOVA

这里是不假定方差齐性的办法，得到的结果
如果是多因素，需要进行两两比较，就需要使用下面的方差操作
GH <- with(ToothGrowth, posthocTGH(len, dosef, method = ‘games-howell’, digits = 3))
GH$output$games.howell

如果不符合正态分布，就需要用到kruskal wallis检验

kruskal wallis.test(len~dosef, ToothGrowth)

事后检验就要用wilcox检验完成
with(ToothGrowth, pairwise,.wilcox,.test(len, dosef, exact = F))

如果多因素有交互作用，需要用到下面的做法完成

AOV2 <- aov(len~dosef*supp, ToothGrowth) 或者写成下面这样
AOV2 <- aov(len~dosef + supp + dosef:supp, ToothGrowth)
summary(AOV2)
说明这两个因子不仅仅有各自的主效应，还有两者的交互作用

一般如果有交互作用的时候，我们就报两者的交互作用，如果交互作用不显著的时候，我们才会各自的报其他两个的结果

诊断模型

现在一样需要对模型进行诊断，对正态性和方差齐性进行检验

然后再对这个数据结果进行两两比较
TurkeyHSD（AOV2， ‘dosef:supp’）

接下来做图看看结果，更加直观


如果显著性都标注出来会特别的乱，那么这里用另外一种方式表示

将两两比较的结果保存
TK<- TurkeyHSD(AOV2, ‘dosef : supp’)
plot(TK)