【论文阅读】Swin transformer解读

---

前言

1. 为什么要做这个研究？
将Transformer的高性能迁移到视觉领域，解决CNN中对于全局信息特征提取的不足。将注意力计算限制在窗口中，引入CNN卷积操作的局部性，节省计算量。
2. 实验方法是什么样的？
Swin Transformer提出hierarchical Transformer，来构建不同尺度的特征金字塔，每一层使用移位窗口将self-attention计算限制在不重叠的局部窗口内，同时通过跨窗口连接增加不同窗口之间的信息交互。
3. 得到了什么结果？
在图像分类、分割任务上都取得了比较好的结果。

Abstract

Swin Transformer可以作为计算机视觉的通用主干。将Transformer从自然语言转到视觉的挑战主要来自两个领域之间的差异，例如视觉实体的比例差异很大，图像中的像素与文本中的文字相比分辨率较高。因此，作者提出了一种hierarchical Transformer，其表示是用移位窗口计算的。移位窗口方案通过将self-attention计算限制在不重叠的局部窗口内，同时还允许跨窗口连接，带来了更高的效率。这种分层体系结构可以在不同尺度上建模，并且在图像大小方面的计算复杂度为$O(N)$。Swin Transformer能够适应广泛的视觉任务，包括图像分类和密集预测任务，如目标检测和语义分割。代码和模型在 https://github.com/microsoft/Swin-Transformer。

1. Introduction

视觉领域长期流行CNN，而自然语言处理（NLP）流行的架构则是Transformer，专为序列建模和转换任务而设计，关注数据中的长期依赖关系。本文试图扩展Transformer的适用性，使其可以作为计算机视觉的通用主干。
作者观察到将Transformer在语言领域的高性能转移到视觉领域的困难可以用两种模式之间的差异来解释。

• 规模差异。与作为Transformer处理的基本元素的单词标记不同，视觉元素在规模上可以有很大的不同，这是一个在目标检测等任务中受到关注的问题。现有的基于Transformer的模型中，tokens都是固定大小的，这种属性不适合视觉应用。
• 图像分辨率高，像素点多。如语义分割等任务需要像素级的密集预测，Transformer难以处理高分辨率图像，因为其self-attention的计算复杂度是图像大小成平方。

针对上述两个问题，作者提出了一种包含滑窗操作、层级设计的Swin Transformer。它构建了分层特征映射，并且计算复杂度与图像大小成线性关系。如图1(a)所示，Swin Transformer从小块(用灰色勾勒)开始，逐渐合并更深的Transformer层中的相邻patch来构建分层表示。有了这些分层特征图，Swin Transformer模型可以方便地利用先进技术进行密集预测，例如特征金字塔网络(FPN) 或U-Net。线性计算复杂度是通过在分割图像的非重叠窗口(用红色标出)内局部计算self-attention来实现的。每个窗口中的patch数量是固定的，因此复杂度与图像大小成线性关系。这些优点使Swin Transformer适合作为各种视觉任务的通用主干，与以前基于Transformer的架构形成对比，后者产生单一分辨率的特征图，并且具有二次复杂度。

Swin Transformer的一个关键设计元素在于其连续的self-attention层之间的移动窗口分区，如图2所示。移动的窗口连接了前一层的窗口，提供了它们之间的连接，显著增强了建模能力(见表4)。这种策略在实际延迟方面也很有效：一个窗口内的所有 query patches共享相同的key集，这有利于硬件中的内存访问。

2. Related Work

2.1 CNN and variants. 略
2.2 Self-attention based backbone architectures. 略
2.3 Self-attention/Transformers to complement CNNs. 略
2.4 Transformer based vision backbones. ViT。

3. Method

3.1 Overall Architecture

图3给出了Swin Transformer架构的概述，展示了小型版本（SwinT）。首先将输入的RGB图像分割成不重叠的patches（类似ViT）。每个patch都被视作“token”，其特征为所有像素RGB值的串联。在这些patches上应用了经过修改的Swin Transformer blocks。为了产生分层表示，随着网络的深入，通过patch合并层来减少patch的数量。

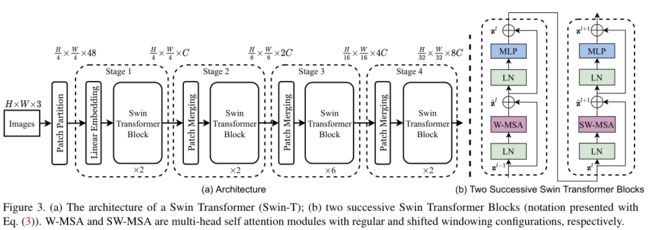
• Stage1：图片尺寸为$H\times W$，设置每个patch的尺寸为$4\times 4$，得到patches数量为$\frac{H}{4}\times \frac{W}{4}$；每个patch有16个像素，RGB图像有3个通道，得到一个patch的特征维度$4\times 4\times 3=48$作为输入的Embedding，再经过一层线性层投影到C维度，这样就得到了$\frac{H}{4}\times \frac{W}{4}\times C$作为第一个Swin Transformer Block的输入。
• Stage2：Patch Merging层将每组2×2相邻的patch特征进行拼接，将4个patch的feature embedding串接起来得到4C的feature，然后接一个线性层得到2C维度特征，再通过Swin Transformer Block进行特征变换，最终输出$\frac{H}{8}\times \frac{W}{8}\times 2C$。
• Stage3：同理，得到输出为$\frac{H}{16}\times \frac{W}{16}\times 4C$。
• Stage4，同理，得到输出为$\frac{H}{32}\times \frac{W}{32}\times 8C$。

这些阶段共同产生分层表示，具有与典型卷积网络相同的特征映射分辨率。这也是为什么作者说可以取代现有视觉方法中的骨干网络。
Swin Transformer block Swin Transformer是通过将Transformer块中的multi-head self attention(MSA)模块替换为基于移位如图3(b)所示，Swin Transformer模块类似由两个连续的Transformer串接起来，区别在于self-attention，前面的使用W-MSA（window multi-head self-attention），靠后的使用SW-MSA（shifted window multi-head self-attention）。后面都接了有GeLU非线性的2层MLP。在每个MSA模块和每个MLP之前应用LayerNorm(LN)层，并且在每个模块之后应用残差连接。

3.2 Shifted Window based Self-Attention

标准的Transformer架构及其对图像分类的适配[ViT]都进行全局self-attention，计算所有token彼此之间的关系。全局计算导致关于token数量的二次方复杂性，使得它不适合许多需要大量token集来进行密集预测或表示高分辨率图像的视觉问题。
Self-attention in non-overlapped windows. 为了高效建模，作者建议在局部窗口内计算self-attention。这些窗口以不重叠的方式均匀地分割图像。假设每个窗口包含$M\times M$个patches，全局MSA模块和基于$h\times w$个patches图像的窗口的计算复杂度为：

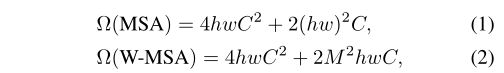
其中，前者与patches数量hw成平方关系，后者在M固定时是线性的（默认情况下设置为7）。全局self-attention计算对于大型硬件来说通常是负担不起的，而基于窗口的self-attention是可扩展的。
MSA复杂度计算：

• 每个patch都要计算对应的$Q、K、V$，而$Q=x\times W^Q，K=x\times W^{，}V=x\times W^V$， 因此需要$3hw{C}^2$；
• 计算patches之间的$Q{K}^T$需要$(hw{)}^{2}C$，与$V$相乘需要$(hw{)}^{2}C$，然后得到的$Z\times W^Z$需要$hw{C}^2$；
• 所以MSA总共需要$4hw{C}^2+2(hw{)}^{2}C$。

W-MSA复杂度计算：

• W-MSA在窗口内做self-attention，共有$\frac{h}{M}\times \frac{w}{M}$个窗口，且每个窗口内计算$Q{K}^T$的复杂度为$(M^2{)}^{2}C$，那么整个图片$Q{K}^T$总共计算复杂度为$M^{2}hwC$，同理与$V$相乘需要$M^{2}hwC$；
• 所以W-MSA总共需要$4hw{C}^2+2M^{2}hwC$。

由于窗口内的patch数量$M^2$远小于整张图片中patch的数量$hw$，W-MSA的self-attention计算只在窗口中，因此W-MSA的计算复杂度和图像尺寸呈线性关系。
Shifted window partitioning in successive blocks. 如果仅仅只在窗口内做self-attention，虽然有效降低了计算复杂度，但是不重合的窗口之间没有信息交流无疑会限制其建模能力。因此，作者引入跨窗口连接，提出了一种移位窗口划分方法（shifted window partition），在两个连续的Swin Transformer块中交替使用W-MSA和SW-MSA。
如图2所示，第一个模块使用常规窗口划分，将一个8×8的特征图按照M=4的窗口大小划分为2×2。然后下一个模块使用shifted的窗口设置，移动$\frac{M}{2}$个像素，得到了3×3个不重合的窗口，移动窗口的划分方法使得上一层相邻的不重合窗口之间有了连接，增大了感受野。
有了shifted结构，swin transformer blocks的计算如下：

其中W-MSA和SW-MSA分别代表使用整齐分割和shifted的多头self-attention；
shifted window可以为模型添加跨windows的连接，并且可以保持模型的高效性，如图4所示；

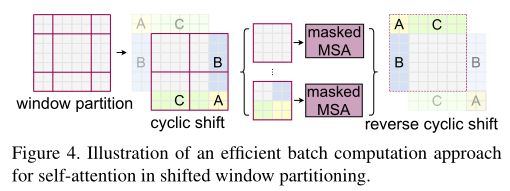
Efficient batch computation for shifted configuration. 移位窗口分割会导致更多的窗口，从$\frac{h}{M}\times \frac{w}{M}$到$(\frac{h}{M}+1)\times (\frac{w}{M}+1)$，并且一些窗口的尺寸将小于$M\times M$。一个解决做法是将较小的窗口填充到$M\times M$的大小，并且在计算注意力时屏蔽填充的值。当规则分区中的窗口数量很小时，使用这种方法增加的计算量很大。作者提出了一种更有效的批处理计算方法，即向左上方循环移位，如图4所示。在这种移位之后，一个批处理窗口可以由特征图上几个不相邻的子窗口组成，因此使用masking机制来将self-attention计算限制在每个子窗口内。通过循环移位，批处理窗口的数量保持与常规窗口划分相同，因此也是有效的。表5显示了这种方法的低延迟。
Relative position bias. 在计算self-attention中的相似度时，对每个头部包含一个相对位置偏差$B\in {\mathbb{R}}^{M^2\times M^2}$。

如表4所示，这带来了明显的性能提升。
关于shifted window的理解

移位操作：图片整体向左和向上分别移动$\frac{M}{2}$个patch，通过torch.roll实现，这样不同窗口就得到了交流。

如果需要reverse cyclic shift的话只需把参数shifts设置为对应的正数值。
Attention Mask
通过设置合理的mask，让Shifted Window Attention在与Window Attention相同的窗口个数下，达到等价的计算结果。
首先我们对Shift Window后的每个窗口都给上index，并且做一个roll操作（window_size=2, shift_size=1）。

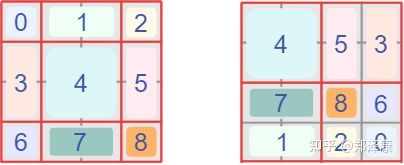
在计算Attention的时候，让具有相同index的QK进行计算，而忽略不同index的QK计算结果。
最后正确的结果如下图所示：

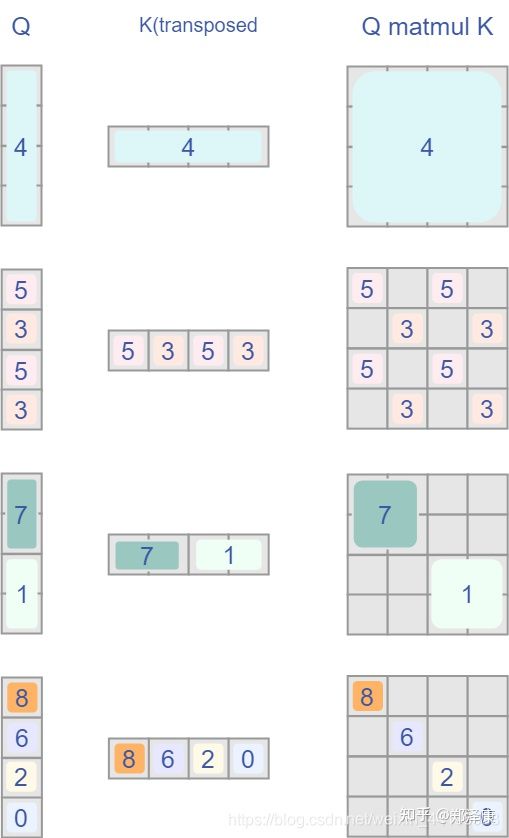
从上面的图可以看到，只保留了相同下标的self-attention结果。
相关代码：

 if self.shift_size > 0:
     # calculate attention mask for SW-MSA
     H, W = self.input_resolution
     img_mask = torch.zeros((1, H, W, 1))  # 1 H W 1
     h_slices = (slice(0, -self.window_size),
                 slice(-self.window_size, -self.shift_size),
                 slice(-self.shift_size, None))
     w_slices = (slice(0, -self.window_size),
                 slice(-self.window_size, -self.shift_size),
                 slice(-self.shift_size, None))
     cnt = 0
     for h in h_slices:
           for w in w_slices:
                 img_mask[:, h, w, :] = cnt
                 cnt += 1

     mask_windows = window_partition(img_mask, self.window_size)  # nW, window_size, window_size, 1
     mask_windows = mask_windows.view(-1, self.window_size * self.window_size)
     attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)
     attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))

以上图的设置，我们用这段代码会得到这样的一个mask。

tensor([[[[[   0.,    0.,    0.,    0.],
           [   0.,    0.,    0.,    0.],
           [   0.,    0.,    0.,    0.],
           [   0.,    0.,    0.,    0.]]],


         [[[   0., -100.,    0., -100.],
           [-100.,    0., -100.,    0.],
           [   0., -100.,    0., -100.],
           [-100.,    0., -100.,    0.]]],


         [[[   0.,    0., -100., -100.],
           [   0.,    0., -100., -100.],
           [-100., -100.,    0.,    0.],
           [-100., -100.,    0.,    0.]]],


         [[[   0., -100., -100., -100.],
           [-100.,    0., -100., -100.],
           [-100., -100.,    0., -100.],
           [-100., -100., -100.,    0.]]]]])

在之前的window attention模块的前向代码里，将mask和原结果相加：

 if mask is not None:
    nW = mask.shape[0]
    attn = attn.view(B_ // nW, nW, self.num_heads, N, N) + mask.unsqueeze(1).unsqueeze(0)
    attn = attn.view(-1, self.num_heads, N, N)
    attn = self.softmax(attn)

将mask加到attention的计算结果，并进行softmax。mask的值设置为-100，softmax后就会忽略掉对应的值。

3.3 Architecture Variants

作者建立了基础模型，称为Swin-B，根据模型大小和计算复杂度，还引入了Swin-T，Swin-S和Swin-L，大概0.25×、0.5×和2×的模型大小和复杂度；其中窗口大小M设置为7，每个头的query维度$d=32$，每个MLP的expansion层$\alpha =4$：

其中C是Stage1中隐藏层的通道数；

4. 实验

图像分类效果超过了ViT、DeiT等Transformer类型的网络，接近CNN类型的EfficientNet。

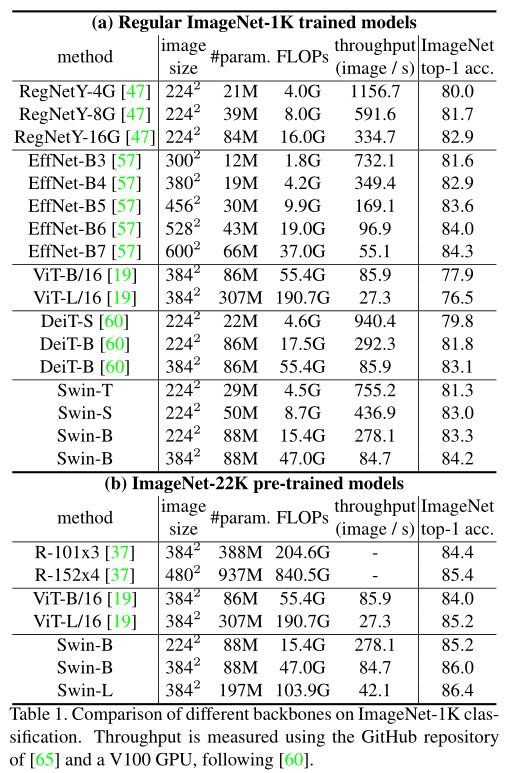
目标检测

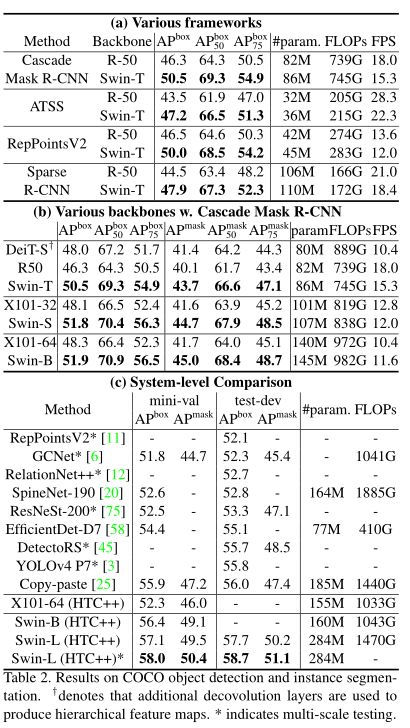
语义分割

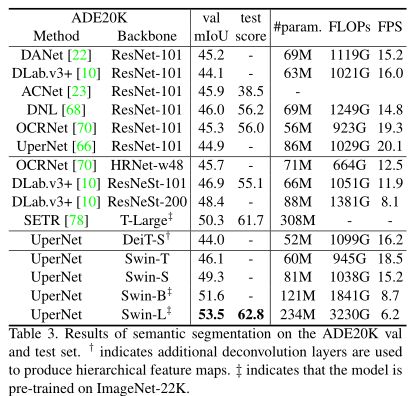
消融实验
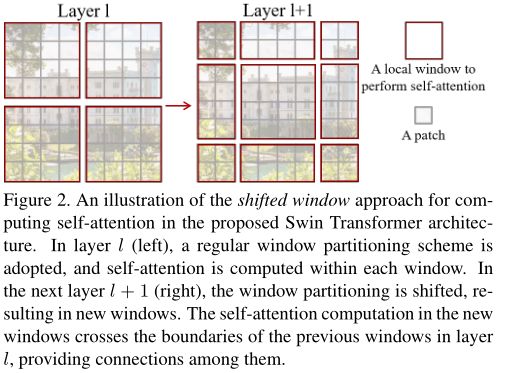
表4，移位窗口操作和添加相对位置偏差的有效性。

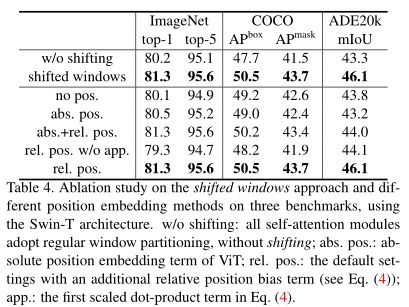
表5，移位窗口和cyclic带的高效性。
表6，使用不同的self-attention比较。

5. 总结

Swin Transformer能够提供分层的特征表示，提出了有效的基于移动窗口的self-attention，并且具有线性计算复杂度。