OpenCV——几何变换原理(python实现和c++实现)
OpenCV图像处理——几何变换原理(python实现和c++实现)
2.1 简介
学习基本的几何变换,几何变换的原理大多都是相似,只是变换矩阵不同,因此,我们以最常用的平移、旋转和翻转为例进行学习。在深度学习领域,我们常用平移、旋转、镜像等操作进行数据增广;在传统CV领域,由于某些拍摄角度的问题,我们需要对图像进行矫正处理,而几何变换正是这个处理过程的基础,因此了解和学习几何变换也是有必要的。
2.2 学习目标
-
了解几何变换的概念与应用
-
理解平移、旋转、翻转的原理
-
掌握在OpenCV框架下实现几何变换操作
2.3 内容介绍
1、平移、旋转、翻转的原理
- 平移
- 旋转
- 翻转
- 复杂的仿射变换
2、OpenCV代码实践
-
c++实现
- 常用函数解析
- 进阶实现(根据原理自己实现)
-
python实现
2.4 算法理论介绍
2.4.1 平移
图像平移就是将图像中所有的点按照平移量水平或者垂直移动。
假设要水平向右侧移动100个像素,向下移动50个像素,则原图像与目标图像的对应关系为:
d s t ( x , y ) = s r c ( x + 100 , y + 50 ) dst(x,y)=src(x+100,y+50) dst(x,y)=src(x+100,y+50)可以转换为:
d s t ( x , y ) = s r c ( x ∗ 1 + y ∗ 0 + 100 , x ∗ 0 + y ∗ 1 + 50 ) dst(x,y)=src(x*1+y*0+100,x*0+y*1+50) dst(x,y)=src(x∗1+y∗0+100,x∗0+y∗1+50)
对应的矩阵变换为:
[ x ′ y ′ 1 ] = [ x y 1 ] [ 1 0 0 0 1 0 100 50 1 ] \begin{bmatrix} x^{'} & y^{'} &1\\ \end{bmatrix} =\begin{bmatrix} x & y & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0\\ 100 & 50 &1 \end{bmatrix} [x′y′1]=[xy1]⎣⎡101000150001⎦⎤
设 t x t_{x} tx和 t y t_{y} ty分别为水平方向和垂直方向偏移量,水平向右为正,垂直向下为正。
所以平移的转换矩阵格式为:
M = [ 1 0 0 0 1 0 t x t y 1 ] M= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0\\ t_{x} & t_{y} & 1 \end{bmatrix} M=⎣⎡10tx01ty001⎦⎤
实际上,在openCV中,只需要传入如下转换矩阵作为参数即可。
M = [ 1 0 t x 0 1 t y ] M= \begin{bmatrix} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \end{bmatrix} M=[1001txty]
2.4.2 旋转
图像旋转是指图像绕着中心转动一定角度的过程,旋转中图像仍保持原始尺寸。图像旋转后图像的水平对称轴、垂直对称轴及中心坐标原点都可能发生变换,因此需要对图像旋转中的坐标进行相应转换。
对于平移,缩放而言,进行变换时以图像的坐标原点(左上角)为基准进行变换即可,但是旋转需要以图像中心为原点,这就需要将图像的坐标进行转换,转换成以中心点为原点的笛卡尔坐标系。
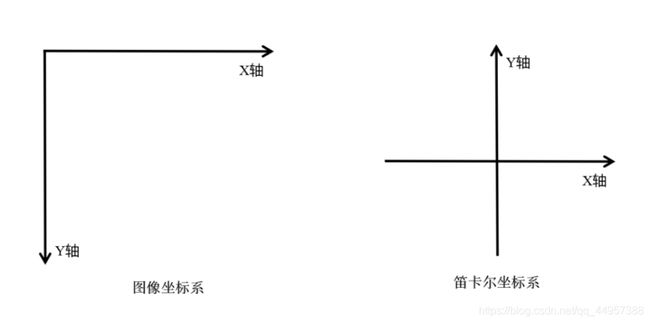
我们知道,图像坐标的原点在图像左上角,水平向右为 X 轴,垂直向下为 Y 轴。数学课本中常见的坐标系是以图像中心为原点,水平向右为 X 轴,垂直向上为 Y 轴,称为笛卡尔坐标系。
图像坐标系与笛卡尔坐标系:
图像坐标系沿 x x x轴向右为正方向,沿 y y y轴向下为正方向。
笛卡尔坐标系沿 x x x轴向右为正方向,沿 y y y轴向上为正方向。
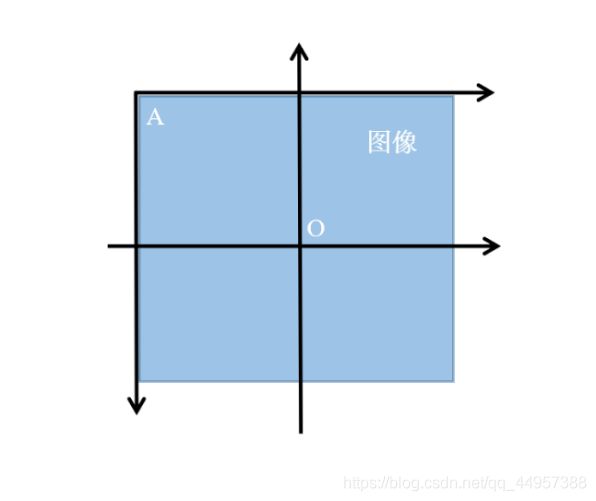
图像坐标系与笛卡尔坐标系转换关系:
图像坐标系的原点为 A A A,而笛卡尔直角坐标系的原点是 O O O。
把一张图像旋转,整个过程可以分为三步:
- 图像坐标系转换为数学坐标系
- 在数学坐标系上进行旋转变换
- 数学坐标系转换为图像坐标系
图像坐标系转换为数学坐标系:
设原图像的为 w i d t h ∗ h e i g h t width*height width∗height的矩阵。
图像的原点坐标 ( 0 , 0 ) (0,0) (0,0)在数学坐标系下变为 ( − w i d t h 2 , h e i g h t 2 ) (-\frac{width}{2},\frac{height}{2}) (−2width,2height)
所以坐标变换可以表示为:
x ′ = x − w i d t h 2 y ′ = − y + h e i g h t 2 x^{'} = x-\frac{width}{2}\\ y^{'} = -y+\frac{height}{2} x′=x−2widthy′=−y+2height
可以对应平移的变换矩阵形式:
M = [ 1 0 0 0 − 1 0 − w i d t h 2 h e i g h t 2 1 ] M= \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0\\ -\frac{width}{2} & \frac{height}{2} & 1 \end{bmatrix} M=⎣⎡10−2width0−12height001⎦⎤
在数学坐标系上进行旋转的坐标变换:
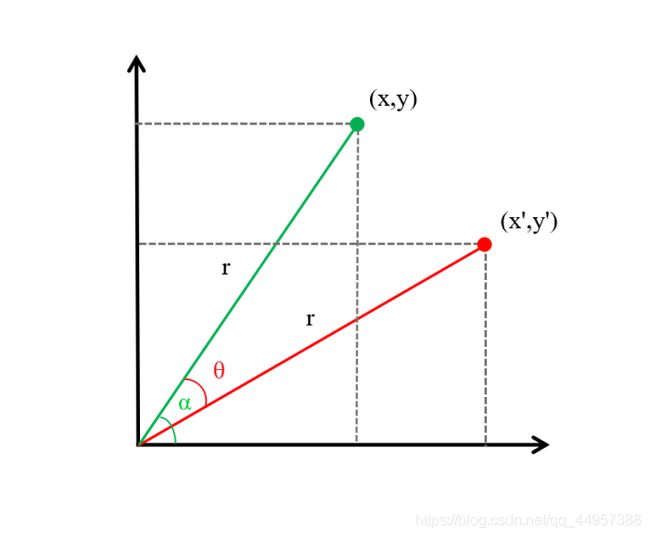
如图,旋转前的坐标为 ( x , y ) (x,y) (x,y),与原点的连线长度为 r r r,与 x x x轴夹角为 α \alpha α
x = r c o s α y = r s i n α x=rcos\alpha\\ y=rsin\alpha x=rcosαy=rsinα
顺时针旋转 θ \theta θ角度后,变为
x ′ = r c o s ( α − θ ) = r ( c o s α c o s θ + s i n α s i n θ ) = x c o s θ + y s i n θ y ′ = r s i n ( α − θ ) = r ( s i n α c o s θ − c o s α s i n θ ) = − x s i n θ + y c o s θ x^{'}=rcos(\alpha-\theta)=r(cos\alpha cos\theta+sin\alpha sin\theta)=xcos\theta+ysin\theta\\ y^{'}=rsin(\alpha-\theta)=r(sin\alpha cos\theta-cos\alpha sin\theta)=-xsin\theta+ycos\theta x′=rcos(α−θ)=r(cosαcosθ+sinαsinθ)=xcosθ+ysinθy′=rsin(α−θ)=r(sinαcosθ−cosαsinθ)=−xsinθ+ycosθ
可以写成以下形式:
[ x ′ y ′ 1 ] = [ x y 1 ] [ c o s θ − s i n θ 0 s i n θ c o s θ 0 0 0 1 ] \begin{bmatrix} x^{'} & y^{'} & 1 \end{bmatrix} =\begin{bmatrix} x & y & 1 \end{bmatrix} \begin{bmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta &0\\ 0 & 0 & 1 \end{bmatrix} [x′y′1]=[xy1]⎣⎡cosθsinθ0−sinθcosθ0001⎦⎤
数学坐标系转换为图像坐标系:
旋转变换后的坐标是数学坐标系,想表示在图像上,还要转换回图像坐标系。转换为数学坐标系的时候,加上的偏移量再减去就可以了。
x = x − w i d t h 2 + w i d t h 2 = x ′ + w i d t h 2 y = − ( − y + h e i g h t 2 ) + h e i g h t 2 = − y ′ + h e i g h t 2 x = x-\frac{width}{2}+\frac{width}{2}=x^{'}+\frac{width}{2}\\ y = -(-y+\frac{height}{2})+\frac{height}{2}=-y^{'}+\frac{height}{2} x=x−2width+2width=x′+2widthy=−(−y+2height)+2height=−y′+2height
转换矩阵为:
M = [ 1 0 0 0 − 1 0 w i d t h 2 h e i g h t 2 1 ] M= \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0\\ \frac{width}{2} & \frac{height}{2} & 1 \end{bmatrix} M=⎣⎡102width0−12height001⎦⎤
将这三步结合起来,一个完整的旋转变换过程可以表示为:
M = [ 1 0 0 0 − 1 0 − w i d t h 2 h e i g h t 2 1 ] [ c o s θ − s i n θ 0 s i n θ c o s θ 0 0 0 1 ] [ 1 0 0 0 − 1 0 w i d t h 2 h e i g h t 2 1 ] M=\begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0\\ -\frac{width}{2} & \frac{height}{2} & 1 \end{bmatrix} \begin{bmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta &0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0\\ \frac{width}{2} & \frac{height}{2} & 1 \end{bmatrix} M=⎣⎡10−2width0−12height001⎦⎤⎣⎡cosθsinθ0−sinθcosθ0001⎦⎤⎣⎡102width0−12height001⎦⎤
[ x ′ y ′ 1 ] = [ x y 1 ] M \begin{bmatrix} x^{'} & y^{'} & 1 \end{bmatrix} =\begin{bmatrix} x & y & 1 \end{bmatrix} M [x′y′1]=[xy1]M
2.4.3 翻转(镜像)
翻转也称为镜像变换,翻转后的图像与原图像是对称的。
翻转分为绕x轴翻转翻转,绕y轴翻转翻转,绕x轴和y轴同时翻转三种情况。
绕x轴翻转,是将图像以x轴为对称轴进行对称变换;
绕y轴翻转,是将图像以y轴为对称轴进行对称变换。
绕x轴和y轴翻转,是将图像以原点为对称中心进行对称变换。
几种翻转情况,目标图像和原图像的坐标关系可以表示如下:
d s t ( x , y ) = { s r c ( w i d t h − x − 1 , y ) 绕 x 轴 翻 转 s r c ( x , h e i g h t − y − 1 ) 绕 y 轴 翻 转 s r c ( w i d t h − x − 1 , h e i g h t − y − 1 ) 绕 x 轴 和 y 轴 翻 转 dst(x,y)=\left\{ \begin{array}{rcl} &src(width-x-1,y) & {绕x轴翻转}\\ &src(x,height-y-1) &{绕y轴翻转}\\ &src(width-x-1,height-y-1) &{绕x轴和y轴翻转}\\ \end{array} \right. dst(x,y)=⎩⎨⎧src(width−x−1,y)src(x,height−y−1)src(width−x−1,height−y−1)绕x轴翻转绕y轴翻转绕x轴和y轴翻转
对应的变换矩阵分别为:
M 0 = [ − 1 0 0 0 1 0 w i d t h − 1 0 1 ] (绕x轴翻转) M_{0}= \begin{bmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ width-1 & 0 & 1 \end{bmatrix}\tag{绕x轴翻转} M0=⎣⎡−10width−1010001⎦⎤(绕x轴翻转)
M + = [ 1 0 0 0 − 1 0 0 h e i g h t − 1 1 ] (绕y轴翻转) M_{+}= \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & height-1 & 1 \end{bmatrix}\tag{绕y轴翻转} M+=⎣⎡1000−1height−1001⎦⎤(绕y轴翻转)
M − = [ − 1 0 0 0 − 1 0 w i d t h − 1 h e i g h t − 1 1 ] (绕x轴和y轴翻转) M_{-}= \begin{bmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ width-1 & height-1 & 1 \end{bmatrix}\tag{绕x轴和y轴翻转} M−=⎣⎡−10width−10−1height−1001⎦⎤(绕x轴和y轴翻转)
2.4.4 复杂的仿射变换
仿射变换能保持二维图形的“平直性”和“平行性”。平直性是指图象经过仿射变换后,直线仍然是直线;平行性是指图像在完成仿射变换后,平行线仍然是平行线。但是仿射变换不能保证原来的线段长度不变,也不能保证原来的夹角角度不变。平移、旋转可以看成简单的仿射变换,他们的角度和线段的相对长度都没变。下面介绍更复杂的仿射变换。
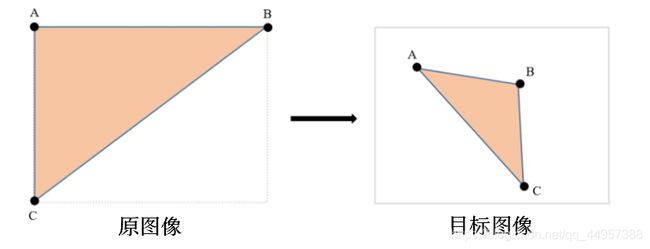
举个例子,下面两个矩形表示两个图像,在原图像和目标图像中分别确定三个点,三个点可以确定一个三角形,也就确定了一个平行四边形。将原图像的三个点仿射到目标图像中的三个点,其余点的映射关系按照指定点的关系计算即可,这样就能确定一个仿射变换。
2.5 基于OpenCV的实现
openCV实现几何变换相关的函数:
- 函数 warpAffine 实现一些简单的变换,如平移,旋转。
- 函数 getRotationMatrix2D 生成转换矩阵。
- 函数 flip 实现图像翻转。
- 函数 getAffineTransform 生成转换矩阵。
2.5.1 c++实现
1、warpAffined函数详解
void cv::warpAffine ( InputArray src,
OutputArray dst,
InputArray M,
Size dsize,
int flags = INTER_LINEAR,
int borderMode = BORDER_CONSTANT,
const Scalar & borderValue = Scalar());
src输入图像,即原图像。dst函数调用后的运算结果存在这里,需和源图片有一样的尺寸和类型。M2×3的变换矩阵。dsize表示输出图像的尺寸。flags插值方式。此参数默认值为INTER_LINEAR(双线性插值)。
可选的插值方式:
INTER_NEAREST - 最近邻插值
INTER_LINEAR - 线性插值(默认值)
INTER_AREA - 区域插值
INTER_CUBIC –三次样条插值
INTER_LANCZOS4 -Lanczos插值
CV_WARP_FILL_OUTLIERS - 填充所有输出图像的像素。如果部分像素落在输入图像的边界外,那么它们的值设定为 0。
CV_WARP_INVERSE_MAP –表示M为输出图像到输入图像的反变换。因此可以直接用来做像素插值。否则, warpAffine函数从M矩阵得到反变换。borderMode边界像素模式,默认值为BORDER_CONSTANT。borderValue边界取值,默认值为0。
注:前面原理部分,转换矩阵为3×3,这里为2×3。
2、getRotationMatrix2D函数详解
C++: Mat getRotationMatrix2D( Point2f center,
double angle,
double scale );center原图像的旋转中心。angle旋转角度。正数表示逆时针旋转,负数表示顺时针旋转。scale缩放系数。
3、flip函数详解
void cv::flip( InputArray src
OutputArray dst,
int flipCode );
src原始图像dst是和原始图像大小,类型相同的目标图像flipCode是旋转类型,0代表绕x轴翻转,任意正数代表绕y轴翻转,任意负数代表x和y轴同时翻转
4、getAffineTransform函数详解
C++:Mat getAffineTransform( const CvPoint2D32f* src,
const CvPoint2D32f* dst,
CvMat* map_matrix );src原始图像的三个点坐标dst输出图像的三个点坐标
该函数中,参数src和dst都是包含三个二维数组 ( x , y ) (x,y) (x,y)的数组,它们定义了两个平行四边形。src和dst中的三个点分别对应平行四边形的左上角、右上角、左下角三个点。由函数getAffineTransform得到的转换矩阵 M M M作为函数warpAffine的参数,将src中的点仿射到dst中。选择三个点,是因为三角形可以表现出变换的尺度和角度。
代码示例(c++)
1、旋转
#include 效果:以图像中心为旋转中心,顺时针旋转45°并缩小为原图像的0.6倍
2、平移
#include 效果:向右移动100个像素,向下移动200个像素
3、翻转
#include 效果:
4、复杂的仿射变换
#include 效果:
进阶实现(根据原理自己实现)
1、旋转(不能放缩,能调整输出图像大小,使原图像不被截断)
/*图像旋转(以图像中心为旋转中心)*/
#include 2、平移
/*平移变换(以图像左顶点为原点)
tx: 水平平移距离 正数向右移动 负数向左移动
ty: 垂直平移距离 正数向下移动 负数向上移动*/
#include 2.5.2 python实现
python中这几个函数和c++的用法和参数几乎一样,只是语法不同
代码示例(python)
1、平移
import cv2
import numpy as np
if __name__ == "__main__":
img = cv2.imread('C:/Users/94890/Desktop/pictures2/yehuimei.jpg', cv2.IMREAD_UNCHANGED)
width,height=img.shape[:2] #记录原图像的行数,列数
trans_mat = np.float32([[1,0,100],[0,1,200]]) #变换矩阵
dst = cv2.warpAffine(img, trans_mat, (width, height)) #平移图像,输出图像为原图像大小
#显示图像
cv2.imshow("origin image", img)
cv2.imshow("move image", dst)
#保存图像
cv2.imwrite("C:/Users/94890/Desktop/pictures2/move.jpg", dst)
cv2.waitKey(0)
cv2.destroyAllWindows()效果:向右移动100个像素,向下移动200个像素
2、旋转
import cv2
import numpy as np
if __name__ == "__main__":
img = cv2.imread('C:/Users/94890/Desktop/pictures2/yehuimei.jpg', cv2.IMREAD_UNCHANGED)
width,height=img.shape[:2] #记录原图像的行数,列数
#变换矩阵,以图像中心为旋转中心,逆时针旋转45°,并将目标图像缩小为原始图像的0.6倍
trans_mat = cv2.getRotationMatrix2D((width/2,height/2),45,0.6)
dst = cv2.warpAffine(img, trans_mat, (width, height)) #输出图像为原图像大小
#显示图像
cv2.imshow("origin image", img)
cv2.imshow("rotation image", dst)
#保存图像
cv2.imwrite("C:/Users/94890/Desktop/pictures2/rotation.jpg", dst)
cv2.waitKey(0)
cv2.destroyAllWindows()效果:以图像中心为旋转中心,逆时针旋转45°并缩小为原图像的0.6倍
3、镜像
import cv2
if __name__ == "__main__":
img = cv2.imread('C:/Users/94890/Desktop/pictures2/Jay.jpg', cv2.IMREAD_UNCHANGED)
width,height=img.shape[:2] #记录原图像的行数,列数
flipx = cv2.flip(img,0)
flipy = cv2.flip(img, 1)
flipxy = cv2.flip(img, -1)
#显示图像
cv2.imshow("origin image", img)
cv2.imshow("flipx", flipx)
cv2.imshow("flipy", flipy)
cv2.imshow("flipxy", flipxy)
#保存图像
cv2.imwrite("C:/Users/94890/Desktop/pictures2/flipx.jpg", flipx)
cv2.imwrite("C:/Users/94890/Desktop/pictures2/flipy.jpg", flipy)
cv2.imwrite("C:/Users/94890/Desktop/pictures2/flipxy.jpg", flipxy)
cv2.waitKey(0)
cv2.destroyAllWindows()效果:
4、复杂的仿射变换
import cv2
import numpy as np
if __name__ == "__main__":
img = cv2.imread('C:/Users/94890/Desktop/pictures2/yehuimei.jpg', cv2.IMREAD_UNCHANGED)
width,height=img.shape[:2] #记录原图像的行数,列数
#分别给定原图像和目标图像中的三个点
p1 = np.float32([[0,0],[width-1,0],[0,height-1]])
p2 = np.float32([[0,height*0.33],[width*0.85,height*0.25],[width*0.15,height*0.7]])
M = cv2.getAffineTransform(p1,p2)#生成转换矩阵
dst = cv2.warpAffine(img,M,(width,height))#生成仿射变换图像
#显示图像
cv2.imshow("origin image", img)
cv2.imshow("dst image", dst)
#保存图像
cv2.imwrite("C:/Users/94890/Desktop/pictures2/dst.jpg", dst)
cv2.waitKey(0)
cv2.destroyAllWindows()效果:
— By: 胖虎
关于Datawhale:
Datawhale是一个专注于数据科学与AI领域的开源组织,汇集了众多领域院校和知名企业的优秀学习者,聚合了一群有开源精神和探索精神的团队成员。Datawhale以“for the learner,和学习者一起成长”为愿景,鼓励真实地展现自我、开放包容、互信互助、敢于试错和勇于担当。同时Datawhale 用开源的理念去探索开源内容、开源学习和开源方案,赋能人才培养,助力人才成长,建立起人与人,人与知识,人与企业和人与未来的联结。