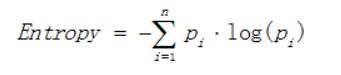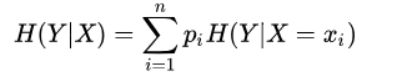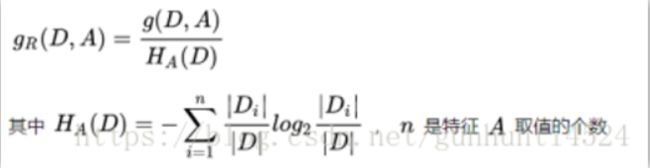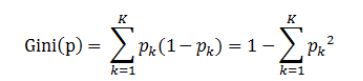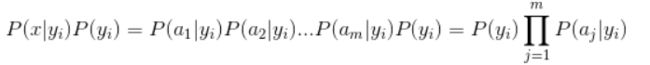《R语言数据挖掘》读书笔记:三、分类
第三章、分类
1.分类(相当于构建一个分类器)
1.1 分类的基本介绍:
给定一个预定义的类标签集合,分类的任务是使用分类器的训练模型,为输入数据集的每个数据对象分配一个标签。通常,输入可能是离散值,也可能是连续值,但输出是离散二进制值或者名义数值等。分类算法通常描述为学习模型或函数。
f(x,y)=0,x=(x1,x2,...,xn)
其中,x是属性集合的元组,集合中的值可以是离散值,也可以是连续值;y具有离散值(如类别标签)的属性。该函数可作为分类模型,可用于判断对象属于哪个类或预测新元组或前面函数中的y值。从另一个角度来看,分类算法是从输入数据中寻找模型,当给定常见属性集合时,应用该模型对未来的类进行预测。
一般而言,分类系统的输入为若干属性的集合,记为x=(x1,x2,...,xn)。有特定的算法用来从这些属性中选择出那些有用的属性,这样可以保证分类系统效率。
1.2 分类预处理方法:数据清洗、相关分析、数据变换或约简
1.3 标准分类过程:
(1)训练(监督学习):依据训练集中的数据建立分类模型。
(2)分类验证:用测试数据集对模型的准确性进行验证,进而决定是否接受模型,选择分类精度较高的模型作为最终的分类器。
2.通用决策树归纳法
决策树的知识总结: https://blog.csdn.net/gunhunti4524/article/details/81506012
正规: https://www.cnblogs.com/csguo/p/7814855.html
全面: https://www.cnblogs.com/yonghao/p/5061873.html
2.1 决策归纳树算法的设计要考虑的问题:
(1)如何在给定节点上对训练集数据进行分裂?树增长的每次递归都必须要选择一个属性测试条件,将记录划分为更小的子集。为了更好的进行记录分割,算法必须为不同类型的属性指定测试条件的方法,并且提供评估每个测试条件优劣的客观标准;
(2)关于模型过度拟合的问题(如何停止分裂?)
①朴素方法:当该节点中的所有数据对象均属于同一类或者所有记录具有相同的属性值时,可根据该节点中的大多数记录对结点分配类标签。
②提前终止算法。
2.2 属性选择度量(选择一些属性用于作为分裂标准)
常用的属性选择度量: https://www.cnblogs.com/muzixi/p/6566803.html
2.2.1 熵(Entropy):用于描述数据集的混乱程度,熵值越高,数据中的不确定性越大。
2.2.2 条件熵(Conditional Entropy): 随机变量X给定的条件下,随机变量Y的条件熵H(Y|X)
其中,pi = P(X = xi)。
2.2.3 信息增益(Information Gain):
信息增益表示的是:得知特征X的信息而使得类Y的信息的不确定性减少的程度。
特征A对训练数据集D的信息增益g(D,A)定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差,即
g(D,A)=H(D)-H(D|A)
一般地,熵H(Y)与条件熵H(Y|X)之差称为互信息(mutual information).即:信息增益也称为互信息。
信息增益的缺点:偏向具有能分割更分散的数据的属性,例如如果划分的属性为product_id,那么最终计算出来的信息熵为0,信息增益最大。但是这种划分是没有意义的。
2.2.4 增益比(Gain Ratio):C4.5分类算法采用,使用信息增益比来选择特征
为了克服信息增益的缺点,采用增益率来作为衡量指标。
主要想法:既然信息增益有偏向大量值的倾向,那么找到一种方法归一化这种大量值属性的信息增益,使所有的信息增益都处在一个公平的度量环境下就好。
定义:信息增益比 = 信息增益 / 划分前熵(后面的分裂信息) 选择信息增益比最大的作为最优特征
2.2.5 Gini指数(Gini Index):基尼指数要求树是二叉树,衡量的是数据集D的不纯度(表示在样本集合中一个随机选中的样本被分错的概率) 详见(上面也有): https://www.cnblogs.com/muzixi/p/6566803.html
定义:基尼指数(基尼不纯度)= 样本被选中的概率 * 样本被分错的概率
其中pk=P(ck▏D) ck是某一样本,D是样本总量
2.2.6 分裂信息(Split Info):就是上面的划分前熵。
2.3 决策树剪枝
初始决策树有太多分支,这些分支反映噪声或者异常值,这也是模型过度拟合的主要原因。对决策树剪枝,以达到更高的分类准确度和更低的错误率。
剪枝策略:后剪枝(在树成长为最大形式后进行树剪枝)、先剪枝(该类剪枝策略也称为提前终止策略,它可以避免过度成熟树的生成,使用一些额外的约束提前终止决策树的生长)
2.4 决策树生成的一般算法
2.5 R语言实现(略)
3.使用ID3算法对高额度信用卡用户分类
ID3决策归纳树设计的最流行算法之一。
该算法不接受缺失值和噪声,属性值必须来自无限固定集合。
ID3算法使用熵来计算样本的均匀性,也用于分裂。使用2.2.3的信息增益计算公式计算每个属性A的信息增益。最终生成的树的根节点包含具有最大信息增益的属性。然后根据根节点的每个属性值,递归地构建新的子树。
3.1 ID3(Iterative Dichotomiser 3 迭代二分器)算法
ID3(C4.5和CART)算法采用贪婪策略(选择信息增益最大的属性作为分类依据)对可能地决策树空间采用自上而下分治方式递归地构建决策归纳树。采用贪婪搜索策略,每一步做出最大改进最优目标地决策。对于每个节点,寻找训练数据在测试条件最佳划分,并将训练数据分配给它。
采用ID3归纳树有以下特性:
(1)除树的叶子节点外,每个节点对应一个输入属性,每条边对应属性的一个可能值。
(2)对于给定数据集,用熵作为指标来衡量使用某一输入属性进行分类后对输出类别的信息量的影响。
(3)递归算法
3.2 R语言实现
关于ID3算法的详细介绍: https://www.cnblogs.com/kuaizifeng/p/9110157.html
3.3 网络攻击检测
入侵检测系统IDS可以使用这种算法,通过特定的变换,ID3算法可以用来对不同大小的数据集进行不同的网络攻击检测。当数据集的大小增加时,ID3算法的性能可通过并行计算保持高效。
3.4 高额度信用卡用户分类
通过选择合适的属性,可以应用ID3算法来最后提取敏感特征或有代表性的特征,据此来帮助判断哪些用户将更有可能成为盈利目标。
4.使用C4.5算法进行网络垃圾页面检测
概述:
C4.5是ID3算法的扩展。与ID3算法相比,C4.5可以更好的处理缺失值、属性值,以及属于无限连续范围内的属性。
C4.5是一种决策树算法,也是一种监督学习分类算法。学习模型并将输入属性值映射到互斥的类标签。而且,学习的模型可以用来对新的未见过的示实例或属性值进行进一步的分类。在该算法中,采用的属性选择度量是增益比,该度量可以避免可能的偏差。
4.1 C4.5算法(剪枝采取后剪枝策略,采用贪婪的学习算法)
关于C4.5算法的详细介绍和实例: https://blog.csdn.net/fuqiuai/article/details/79456971
基于通用的C4.5算法,派生出了许多算法,如C4.5、无剪枝的C4.5(C4.5-no-pruning)、C4.5规则(C4.5rule)等,这些算法统称为C4.5算法
4.2 R语言实现(略)
4.3 基于MapReduce的并行版本
随着数据集容量或大小的不断增长,C4.5算法可以借助MapReduce算法、Hadoop技术套件,特别是通过R语言的RHadoop,并行实现。
4.4 网络垃圾页面检测
C4.5算法应用:可以用作垃圾页面分类器以便区分垃圾页面与正常页面。在所有的分类算法中C4.5算法的性能最好。
5.使用CART算法判断网络关键资源页面
分类和回归树(Classification and Regression Tree ,CART)是最流行的决策树算法之一。
该算法是一个二元递归分割算法,他可以用来处理连续属性和名义属性。
5.1 CART算法
主要是根据上面这个公式找到最大值,就是特征A取α时作为分裂点的最优情况。
该算法主要由三个步骤组成:构建最大树(二叉树)、选择合适的树大小、最后使用生成的决策树对数据进行分类。
CART算法生成一系列的候选决策树,这些候选决策树在经过一系列的嵌套式修剪产生唯一的最优决策树,该最优决策树作为最终的结果。
CART算法原理与实现详细解析: https://www.cnblogs.com/gswang/p/7513299.html
5.2 R语言实现(略)
5.3 网络关键资源页面判断(CART算法应用)
6.木马程序流量识别方法和贝叶斯分类
贝叶斯分类时概率分类算法,它基于贝叶斯定理。贝叶斯分类器通过使后验概率达到最大来对相应的实例或类进行预测。贝叶斯分类的风险在于该算法需要足够的数据才能对联合概率密度进行可靠的估计。
贝叶斯分类器的基本方法:在统计资料的基础上,依据找到的一些特征属性,来计算各个类别的概率,找到概率最大的类,从而实现分类。
6.1 贝叶斯定理
条件概率定义:
事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”。
还需要用到似然估计的知识:P(A|Bi)是类条件概率,有可能是未知的,要通过样本选择合适的似然估计方法确定参数
贝叶斯定理是根据已有的统计资料预测某情况在一定条件下可能发生的概率。(小例子见下方网址“看病”)
贝叶斯推断的含义:我们先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。
6.2 贝叶斯分类
贝叶斯分类算法的详细解析: https://www.cnblogs.com/csguo/p/7804355.html
极大似然估计在贝叶斯决策里的应用: https://blog.csdn.net/qq_39355550/article/details/81809467
基本思想是:根据贝叶斯定理,给定一个x值(相当于需要判断属于哪一类的某种情况),使概率值最大,得到当取最大值时属于哪个类,从而实现分类情况,主要还是根据已有的统计资料下进行判断分类。(具体看上面网址的“贝叶斯分类的定义和例子”)
6.3 R语言实现(略)
6.4 木马流量识别方法
木马分为多种类型,每种类型均具有某种流量行为。通过识别木马流量,可以进一步处理来保护信息。检测系统中的木马的一个重要行为就是检测木马流量。DNS流量在木马检测中起着重要作用,木马流量与DNS流量有着一定的关系。贝叶斯分类器可以用于检测异常值,判断木马软件。
7.垃圾邮件识别和朴素贝叶斯分类
7.1 朴素贝叶斯分类
朴素贝叶斯分类假定所有的属性都是独立的,它简化了贝叶斯分类且不需要相关的概率计算。可以通过以下公式计算似然概率
式中ai为属性值
朴素贝叶斯分类的特征:对孤立噪声具有鲁棒性、对不相关属性具有鲁棒性、由于受到输入数据具有相关性的属性的影响,性能可能下降。
具体算法和贝叶斯算法相似,参看上述网址。
7.2 R语言实现(略)
7.3 垃圾邮件识别(朴素贝叶斯算法的应用)
邮件的属性,如主题、内容、发送者地址、IP地址、与时间相关的属性等可作为数据集中数据实例的属性集。就相当于ai
朴素贝叶斯分类器的训练数据集由标记为垃圾邮件和合法的邮件组成。
8.基于规则的计算机游戏玩家类型分类和基于规则的分类
基于规则的分类学习模型是由IF-THEN规则集建立的。这些规则可以从决策树变换而来,也可以根据算法给出。
IF-THEN规则的格式:IF 条件成立 THEN 得出结论 另一种格式:规则前件<—规则后件
对于给定的数据集中的实例或记录,如果规则前件为真,则定义规则覆盖该实例,或实例符合该规则。
给定规则R
规则的覆盖率:Coverage(R)=| Dcover | / | D |
规则的准确率:Accuracy(R)=|Dcorrect|/|Dcover|
8.1 从决策树变换为决策规则
决策树可以很方便地变换为决策规则。沿着决策树中从根节点到叶子结点的每一条路径可以写一条决策规则。规则的左边(规则前件),可以通过组合不同节点和连线的标签得到,规则后件即为对应的叶子节点。
8.2 基于规则的分类
采用贪婪策略,它的目标是最大可能地覆盖源数据集中的正实例,同时使得其中负实例数尽量少甚至没有。
源数据集中具有给定类的所有实例定义为正实例,而属于其他类的实例定义为负实例。
思想:算法首先产生一条初始规则r,然后通过不断改进r知道满足停止条件。
8.3 序列覆盖算法(也是基于规则的)
对于初始空的规则集,逐渐加入规则,直至结束条件,得到的就是分类规则
顺序覆盖算法详解: https://www.cnblogs.com/leeshum/p/4876025.html
8.4 RIPPER算法(Repeated Incremental Pruning to Produce Error Reduction)
该算法是直接基于规则的分类器,规则集更容易解释,更适于解决不平衡问题。
当规则生长时,算法从空规则开始,添加连接词,它最大化或改进信息增益度量,即FOIL。当算法结束时,规则不包含负规则(即不冗余)。随后,立即对得到的规则应用逐步降低误差剪枝法进行剪枝。
RIPPER算法详解(结合上面网址,基于规则的算法实例): https://www.cnblogs.com/hgz-dm/p/10886175.html
8.5 计算机游戏玩家类型的基于规则的分类
基于玩家行为或模型,可以用数据集训练决策树模型,并从训练后的决策树模型得到规则集合。数据集可以来自游戏日志或某些预定义的领域知识。
下一章将介绍几种高级分类算法,包括贝叶斯信念网络、支持向量机、K近邻算法等