八大排序算法面试详解（最全版）

排序算法的重要性

排序特别重要，出场频率极高的面试题，但是实际工作中一般不会去手写排序（标准库中有现成的排序方式），都是未来找工作中经常遇到的问题，都是重点，代码都非常重要，就算是背也得背下来。

排序规则

一般是升序和降序，如果待排序元素比较复杂，就会有更复杂的排序方式。（比如：手握多个offer,该怎么选取offer:可以：1：薪资排第一:2：业务排第二:3：工作地点排第三（北》深》上》==杭》广》其他）:4：公司规模，团队情况，伙食情况次之）

排序算法

插入排序

基于前面讲过的顺序表插入来实现的。

package Java0420;

import java.util.Arrays;
public class TestSort {
     
    public static void insertSort(int[] array){
     //插叙排列，升序排序
        //通过 bound 来划分出两个区间
        //[0,bound)已排序区间
        //[bound,size)待排序区间
        for(int bound = 1;bound < array.length;bound++){
     
            int v = array[bound];
            int cur = bound - 1;//已排序区间的最后一个元素下标
            for(;cur >= 0;cur--){
     
                if(array[cur] > v){
     
                    array[cur + 1] = array[cur];
                } else {
     
                    //此时说明已经找到了合适的位置
                    break;
                }
            }
            array[cur + 1] = v;
        }
    }

    public static void main(String[] args) {
     
        int[] arr = {
     9,5,2,7,3,6,8};
        insertSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

插入排序：
时间复杂度：O（N^2）
空间复杂度：O（1）
稳定性：稳定排序
插入排序两个重要特点：

1. 当待排序区间元素比较少的时候，排序效率很高
2. 当整个数组比较接近有序的时候，排序效率也很高

---

希尔排序

可以将它理解为进阶版本的插入排序。先分组，针对每个组进行插入排序，组件缩小组的个数，最终整个数组就接近有序了。

比如：

public static void shellSort(int[] array){
     
        int gap = array.length / 2;
        while (gap > 1){
     
            //需要循环进行分组插排
            insertSortGap(array,gap);
            gap = gap / 2;
        }
        insertSortGap(array,1);
}
private static void insertSortGap(int[] array,int gap) {
     
        for(int bound = gap;bound < array.length; bound++){
     
            int v = array[bound];
            int cur = bound - gap;//这个操作是在找同组中的上一个元素
            for (;cur >= 0; cur -= gap){
     
                if (array[cur] > v){
     
                    array[cur + gap] = array[cur];
                } else {
     
                    break;
                }
            }
            array[cur + gap] = v;
        }
}

选择排序

选择排序：基于打擂台的思想，每次从数组中找出最小值，然后把最小值放到合适的位置上。

选择排序代码实现：

public static void selectSort(int[] array) {
     //选择排序
        for (int bound = 0; bound < array.length; bound++) {
     
            //以bound位置的元素作为擂主，循环从待排序区间中取出元素和擂主进行比较，如果打擂成功，就和擂主交换
            for(int cur = bound + 1; cur < array.length;cur++){
     
                if(array[cur] < array[bound]) {
     
                    //打擂成功
                    int tmp = array[cur];
                    array[cur] = array[bound];
                    array[bound] = tmp;
                }
            }
        }
}

堆排序

堆排序代码实现：

private static void swap(int[] array,int i,int j) {
     
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
}
public static void heapSort(int[] array) {
     //堆排序
        //先建立堆,面试的时候也建议大家单独写一个建堆方法。
        createHeap(array);
        //循环把堆顶元素交换到最后，并进行调整堆,循环次数是 length - 1,当堆中只剩一个元素的时候，也就一定是有序的，不需要再继续进行循环调整了
        for (int i = 0; i < array.length - 1;i++) {
     
            //交换堆顶元素和堆的最后一个元素
            //堆的元素个数相当于 array.length - i
            //所以堆的最后一个元素下标就是：array.length - i - 1;
           swap(array,0,array.length-1-i);//此处最后一个元素每一步是不一样的
            //交换完成之后，要把最后一个元素从堆中删掉
            //交换之后，对的长度就又进一步缩水了array.length - i - 1
            /*数组中，就划分出了两个区间：
            * 1：[0,array.length - i - 1) 待排序期间
            * 2：[array.length - i - 1,array.length) 已排序区间
            * */
            shiftDown(array,array.length - i - 1,0);//进行向下排序
        }
}

    private static void createHeap(int[] array) {
     
        //从最后一个非叶子节点出发向前循环，依次进行向下调整
        for (int i = (array.length - 1 - 1) / 2;i >= 0;i--) {
     
            shiftDown(array,array.length,i);
        }
    }

    private static void shiftDown(int[] array, int heapLength, int index) {
     
        //这里咱们是升序排序，建立的是大堆，大堆就需要找出左右子树中的较大值再和根节点比较
        int parent = index;
        int child = 2 * parent + 1;
        while (child < heapLength) {
     
            if (child + 1 < heapLength && array[child + 1] > array[child]) {
     
                child = child + 1;
            }
            //条件结束意味着，child就已经是左右子树比较大的值的下标了
            if(array[child] > array[parent]){
     
                //需要交换两个元素
                swap(array,child,parent);
            } else {
     
                break;
            }
            parent = child;
            child = 2 * parent + 1;
        }
    }

冒泡排序

冒泡排序代码实现：

    public static void bubbleSort(int[] array) {
     
        //按照每次找最小的方式来进行排序。（从后往前比较交换）
        for (int bound = 0; bound < array.length;bound++) {
     
            //[0,bound)已排序区间，[bound,size)待排序区间
            for (int cur = array.length - 1;cur > bound;cur--) {
     
                if (array[cur - 1] > array[cur]) {
     
                    swap(array,cur - 1,cur);
                }
            }
        }
    }

快速排序

快速排序的递归和非递归实现：

 public static void quickSort(int[] array) {
     
        quickSortHelper(array,0,array.length - 1);//辅助完成递归过程，此处为了代码简单，区间设定成前闭后闭。


    }

    private static void quickSortHelper(int[] array, int left, int right) {
     
        if (left >= right) {
     
            //区间中有0个元素或者1个元素，此时不需要排序
            return;
        }
        //针对[left,right)区间进行整理
       int index = partition(array,left,right);//index返回值就是整理完毕后，left 和right的重合位置，知道了这个位置，才能进一步进行递归
        quickSortHelper(array,left,index-1);
        quickSortHelper(array,index + 1,right);
    }

    private static int partition(int[] array, int left, int right) {
     
        int i = left;
        int j = right;
        int base = array[right];
        while (i < j) {
     
        //从左往右找到比基准值大的元素
            while (i < j && array[i] <= base) {
     
                i++;
            }
            //当上面的循环结束时，i 要么和j 重合，要么i就指向一个大于base的值
            //从右往左找比基准值小的元素
            while (i < j && array[j] >= base) {
     
                j--;
            }
            //当上面的循环结束之后，i要么和j重合，要么j就指向一个小于base的值
            //交换i和j的值
            swap(array,i,j);
        }
        //当i和j重合的时候，最后一步，要把重合位置的元素和基准值进行交换
        //[思考] 为啥下面交换了之后，仍然能满足快排的顺序要求呢？
        /*
        right这是一个序列中最后的位置，就要求i,j重合位置的元素必须是大于等于基准值的元素，才可以放到最后面
        * 如何证明找到的i位置的元素一定 >= 基准值呢？
        * a)i++导致和j重合
        * 此时最终的值取决于上次循环中j指向的值，上次循环中，j应该是找到了一个小于基准值的元素，然后和一个大于基准值的元素交换了
        * ，此处最终的j一定是大于基准值的元素
        * b)j--导致和i重合
        * 此时上面i++的循环退出就一定是因为i位置找到了一个比基准值大的元素，j和i重合最终元素也一定大于等于基准值
        * */
        swap(array,i,right);
        return i;
    }
public static void quickSortByLoop(int[] array) {
     //用非递归的方式实现快速排序
        //借助栈模拟实现递归的过程
    Stack<Integer> stack = new Stack<>();//stack用来存放数组下标，通过下标来表示接下来要处理的区间是啥
        //初始情况下，先把右侧边界下标入栈，再把左侧边界下标入栈，左右边界仍然构成前闭后闭区间
    stack.push(array.length - 1);
    stack.push(0);
    while (!stack.isEmpty()) {
     
        int left = stack.pop();//这两个代码的顺序要和入栈的顺序对应
        int right = stack.pop();
        if (left >= right) {
     
            //区间中只有一个或0个元素，不需要整理
            continue;
        }
        //通过partition把区间整理成以基准值为中心，左侧小于等于基准值，右侧大于等于基准值的形式
      int index =   partition(array,left,right);
        //准备处理下个区间,[index + 1,right]基准值右侧区间
        stack.push(right);
        stack.push(index + 1);
        //[left,index - 1]基准值左侧区间
        stack.push(index - 1);
        stack.push(left);

    }
    }

快速排序的优化方法：

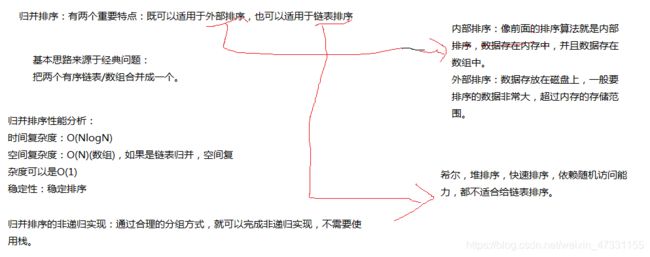
归并排序

归并排序代码实现：

    /*
    [low,mid)有序区间
    [mid,high)有序区间
    把这两个有序区间合并成一个有序区间
    */
    public static void merge(int[] array,int low,int mid,int high) {
     
        int[] output = new int[high - low];
        int outputIndex = 0;//记录当前output数组中被放入多少个元素了
        int cur1 = low;//第一个区间的起始下标
        int cur2 = mid;//第二个区间的起始下标
        while (cur1 < mid && cur2 < high) {
     
            if (array[cur1] <= array[cur2]) {
     //这里写成<=才能保证稳定性
                output[outputIndex] = array[cur1];
                outputIndex++;
                cur1++;
            } else {
     
                output[outputIndex] = array[cur2];
                outputIndex++;
                cur2++;
            }
        }
        /*
        * 当上面的循环结束的时候，肯定是cur1 或者 cur2 有一个先到达末尾，另一个还剩下一些内容，把剩下的内容都一股脑
        * 拷贝到output中*/
        while (cur1 < mid) {
     
            output[outputIndex] = array[cur1];
            outputIndex++;
            cur1++;
        }
        while (cur2 < high) {
     
            output[outputIndex] = array[cur2];
            outputIndex++;
            cur2++;
        }
        //把output中的元素再搬运回原来的数组
        for (int i = 0;i < high - low; i++) {
     
            array[low + i] = output[i];
        }
    }
    public static void mergeSort(int[] array) {
     
        mergeSortHelper(array,0,array.length);//构造一个辅助递归的方法
    }
    /*
    * [low,high)前闭后开区间，如果两者差值小于等于1,区间中就只有0个元素或者1个元素
    * */
    private static void mergeSortHelper(int[] array, int low, int high) {
     
        if(high - low <= 1){
     
            return;
        }
        int mid = (low + high) / 2;
        mergeSortHelper(array,low,mid);//这个方法执行完，就认为low,mid已经排序ok
        mergeSortHelper(array,mid,high);//这个方法执行完，就认为，mid，high已经排序ok
        /*
        * 当把左右区间已经归并排序完了，说明左右区间已经是有序区间了，接下来就可以针对两个有序区间进行合并了*/
        merge(array,low,mid,high);
    }
    =================================================
    public static void mergeSortByLoop(int[] array) {
     //用非递归的方式实现归并排序
        //引入一个gap变量进行分组
    // 当gap为1的时候，[0,1)和[1,2)进行合并，[2,3)和[3,4)进行合并，[4,5)和[5,6)进行合并......
    //当gap为2的时候，[0,2) 和 [2,4)进行合并，[4,6)和[6,8)进行合并......
    //当gap为4的时候，[0,4) 和 [4,8)进行合并......
    for (int gap = 1;gap < array.length; gap *= 2) {
     
        //接下来进行具体的分组合并,下面的循环执行一次，就完成了一次相邻两个组的合并
        for (int i = 0; i < array.length; i += 2*gap) {
     
            /*当前相邻组，[beg,mid)  [mid,end)
            * */
            int beg = i;
            int mid = i + gap;
            int end = i + 2*gap;
            //防止下标越界
            if (mid > array.length) {
     
                mid = array.length;
            }
            if (end > array.length) {
     
                end = array.length;
            }
            merge(array,beg,mid,end);
        }
    }
    
}

其他排序

还有很多其他类型的排序，比如以下之类的等等：