P3:线性分类、损失函数与梯度下降
子豪兄YYDS:
https://www.bilibili.com/video/BV1K7411W7So?p=3
一、线性分类器
线性分类器,确定一条直线,让用例可以分为两类,线性分类器的关键在于一个合适的权重,利用这个权重,可以将图片转换为一个计算的结果,这个结果是一个数字,可以看做一张图片在一个权重下的得分,而每个分类器有自己的一个权重,这样就可以把每个分类器的权重看做一个考试,这样计算的结果就是在一次考试中的得分。根据得分情况确定是不是这个类别。理想情况下这个得分是越大越好,但是在训练过程中存在误差和判断错误的情况,需要经过对损失函数进行梯度下降法优化权重,来不断修正模型,最终让得分越大越好。
二、两类损失函数:铰链损失函数和交叉熵损失函数
铰链损失函数Hinge Loss是一种损失函数,通常被用于最大间隔算法,这个算法又常用在SVM支持向量机中,这个损失函数的计算是基于线性分类器的得分,计算分类错误的得分与分类正确的得分的差值加一,比较这个数和0的大小,取最大值:

计算这个数之后将每个图片的值相加作为最终的损失函数。
从这个函数的值域来看,最小值是0最大值可以是正无穷,既然最小是0,那么最小化的目标就是让差值在正数的情况下最小,即分类正确-分类错误>1,这样一看就是让分类正确的得分和分类错误的得分尽可能差的更大,换句话说这个损失函数是在惩罚和正确分类得分足够近的样例,这样在后面的调整权重的部分,就可以利用梯度下降法,让权重向着扩大差别的方向调整,让彼此的分类界限更加明显。
正则化项是在损失函数上附加的一个项,这个项主要是用来防止学习到一些没用的内容,防止产生过拟合,筛选出雨露均沾的模型:
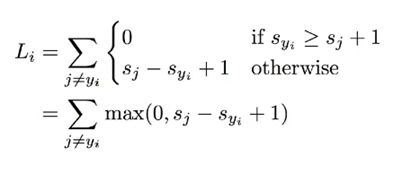

下面的这个例子很好地体现了正则化项的用处:
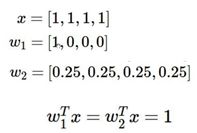
这个例子中,两个权重计算得到的分值是一样的,但是从权重来看,w1完全考虑第一个项的值,而完全不考虑剩下的三个项,但w2是同时考虑了四个项,显然是w2更好,但不考虑正则化的情况下会认为这两个一样,引入正则化项之后,选用L2正则项,显然是w2的损失函数更小,就可以选出更优秀的w2。另外正则化项有一个参数λ,这个参数可以看做正则化的强度,即正则化项对整体损失函数的影响程度。
Softmax是一个函数,用于在保留单调性的同时将得分转换为概率,计算的方法如下:

利用这个函数,我们将一张图片在各个分类上的得分转换为了一个概率值,这个概率值表示分类正确的概率,因为概率值常作为损失函数的输入,所以Softmax是一个很常用的数学工具。
在Softmax函数的基础上,延伸出负对数函数,也就是将Softmax的函数值作为输入,送入负对数函数中。基于负对数函数又延伸出交叉熵损失函数,这个损失函数采用负对数函数,主要还是出于化简的目的。
首先交叉熵损失函数也叫做最大似然估计函数,这个损失函数的思路和最大似然估计是相关联的,它的目的是让概率最大化,而在最大似然估计中,多个无关类别的联合概率是做乘法,乘法显然不如加法,而对数可以将乘法转换为加法,所以在Softmax输出的基础上套了一个对数,但是概率是在0-1之间的,对数的结果是负数,所有概率的对数和依然是一个负数,最大化一个负数等于最小化一个正数,只需要加上一个对号,所以最后变成了负对数,交叉熵损失函数就是将每个图片分类正确的概率的负对数求和作为损失函数,引入权值的修正从而让整体最小,也就是让分类正确的概率最大化。
三、梯度下降法
梯度下降法是用于参数调整的很常用的方法,其核心思想是向着变化的反方向移动一小段距离,从而让整体向着最小值的方向移动。使用过程中首先设定一个参数的初始值,利用损失函数,写出对每个参数的偏导数,在初始值的基础上,向着导数的反方向移动步长的距离,最后得到了这一次参数的更新值,不断重复这个过程,参数将向着损失函数最小值的方向不断移动,从而实现最小化损失函数的目的。
梯度下降法中,存在数据量比较大的情况,此时如果用所有的数据计算梯度,也就是计算全局梯度,计算量会很大,如果是一千万张图片的数据集,那么在全部计算梯度时,需要计算包含一千万个矩阵的损失函数和对每个参数的梯度和偏导数,这样是不合适的,合适的做法是将一小部分的数据的梯度值,对这部分进行梯度下降法去更新权重,这部分数据可能会存在一定的不足,但是每次走一小步依然可以收敛到比较好的程度,这种方式是衡量了计算时间和效果的最优选择。
这里展开来说,如果是将全部数据都用于更新梯度,采用下面的损失函数:
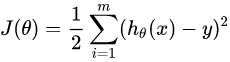
![]()
这种情况下,每次更新首先要计算当前权值下的梯度值,这个梯度值是将权值带入损失函数的梯度,之后再在上次计算的结果上更新计算结果。在更新的过程中,将全部数据带入计算必然会导致计算梯度时的耗时增加,因为梯度中含有一个求和,这个和是一千万个数据相加。梯度函数是从头用到尾的,只不过每次都是代当前的点进去计算。
如果只选择一个数据进行用于梯度的更新,也就是上面的损失函数中m取1,这种情况下称为随机梯度下降,这种方式加快了每次迭代的计算速度,但是也带了收敛不稳定的缺陷。折中方式是下面的小批量梯度下降。
如果是小批量梯度下降,就是选择一部分的数据用于更新,这时也需要计算许多的损失函数和许多的梯度,但是数目少了很多,在求和的部分就只需要计算小部分的数据的和,所以更新迭代的速度也快了,虽然数据不如原来那么丰富,但是胜在速度快。在批量梯度下降中,所有的样本都有贡献,就是说所有的样本都参与了参数Θ的调优,计算得到的是一个标准的梯度,而对于随机梯度下降,并没有采用所有的样本,而是选取了样本的一部分来近似全部的样本,不可否认这种做法存在问题,每次的移动方向不一定向着真正的全局最优方向移动,但是这种方法速度更快,收敛更快,结果在可以接收范围内。
更新过程中的每一步都计算出了从上次的点开始Θ应该移动的方向,更新后的Θ并不参与实际的运算,仅计算后作为下一次的移动原点,最后一次更新,得到的Θ的值就是模型需要的参数。
关于三种梯度下降法,我又结合另一个网站的代码仔细看了一下:
http://sofasofa.io/tutorials/python_gradient_descent/index.php
这个网站用Python实现了三种梯度下降法,从代码本身来看其实区别没有那么大,代码的结构都是一样的,代码主要是三个函数加上循环计算,三个函数分别是计算梯度、更新参数和计算损失值。计算梯度实际上就是带入数据计算,将梯度的更新公式写出来,需要带入的内容包括当前的参数和数据,利用这些计算出当前参数下的梯度。更新参数就是让当前参数向反梯度方向移动步长距离。计算损失值用于判断什么时候收敛到可以结束的程度。在每次计算中,先根据当前的参数值计算当前梯度,更新参数值并检验是否满足收敛条件,不满足则继续计算。
区别在于计算梯度的函数,全批量梯度下降法是将全部数据都用来更新权重,所以在计算梯度的时候,带入了全部的数据,所以计算梯度函数应该是下面的格式:
def compute_grad(beta, x, y):
grad = [0, 0]
grad[0] = 2. * np.mean(beta[0] + beta[1] * x - y)
grad[1] = 2. * np.mean(x * (beta[0] + beta[1] * x - y))
return np.array(grad)
# 计算当前权值下的梯度
这段代码中,beta是当前的参数值,x和y是很长很长的一大串数据,是两列超多行的数据,利用numpy进行了快速的计算。完整版的代码如下:
# 自变量x为id 因变量y为question
# 回归模型为简单的y=β0+β1x
# 误差函数为均方误差函数
import pandas as pd
import numpy as np
train = pd.read_csv('data/train.csv')
test = pd.read_csv('data/test.csv')
submit = pd.read_csv('data/sample_submit.csv')
# 读取训练集和测试集
beta = [1, 1]
# 初始化参数
alpha = 0.2
# 步长
tol_L = 0.1
# 变动阈值
max_x = max(train['id'])
x = train['id'] / max_x
# 筛选出自变量x 并且对x进行归一化
y = train['questions']
# 筛选出因变量y
def compute_grad(beta, x, y):
grad = [0, 0]
grad[0] = 2. * np.mean(beta[0] + beta[1] * x - y)
grad[1] = 2. * np.mean(x * (beta[0] + beta[1] * x - y))
return np.array(grad)
# 计算当前权值下的梯度
def update_beta(beta, alpha, grad):
new_beta = np.array(beta) - alpha * grad
return new_beta
# 更新参数
def rmse(beta, x, y):
squared_err = (beta[0] + beta[1] * x - y) ** 2
res = np.sqrt(np.mean(squared_err))
return res
# 更新rmse
grad = compute_grad(beta, x, y)
# 计算当前梯度
loss = rmse(beta, x, y)
beta = update_beta(beta, alpha, grad)
# 更新beta值
loss_new = rmse(beta, x, y)
# 确定结束计算的条件
i = 1
while np.abs(loss_new - loss) > tol_L:
# 迭代计算
beta = update_beta(beta, alpha, grad)
# beta向着最小方向移动一段距离
grad = compute_grad(beta, x, y)
# 计算新位置下的梯度
loss = loss_new
loss_new = rmse(beta, x, y)
# 更新退出条件
i += 1
print('Round %s Diff RMSE %s'%(i, abs(loss_new - loss)))
print('Coef: %s \nIntercept %s'%(beta[1], beta[0]))
随机梯度下降则是在全批量梯度下降的基础上做的修改,将用于计算梯度的数据量变为一个,每次随机筛选出一个用于计算梯度,代码上只需要修改一行:
def compute_grad_SGD(beta, x, y):
grad = [0, 0]
r = np.random.randint(0, len(x))
# 体现随机梯度下降 只选择一个作为更新的依赖
grad[0] = 2. * np.mean(beta[0] + beta[1] * x[r] - y[r])
grad[1] = 2. * np.mean(x[r] * (beta[0] + beta[1] * x[r] - y[r]))
return np.array(grad)
# 计算当前权值下的梯度
完整代码如下:
# 自变量x为id 因变量y为question
# 回归模型为简单的y=β0+β1x
# 误差函数为均方误差函数
import pandas as pd
import numpy as np
train = pd.read_csv('data/train.csv')
test = pd.read_csv('data/test.csv')
submit = pd.read_csv('data/sample_submit.csv')
# 读取训练集和测试集
beta = [1, 1]
# 初始化参数
alpha = 0.2
# 步长
tol_L = 0.1
# 变动阈值
max_x = max(train['id'])
x = train['id'] / max_x
# 筛选出自变量x 并且对x进行归一化
y = train['questions']
# 筛选出因变量y
def compute_grad_SGD(beta, x, y):
grad = [0, 0]
r = np.random.randint(0, len(x))
# 体现随机梯度下降 只选择一个作为更新的依赖
grad[0] = 2. * np.mean(beta[0] + beta[1] * x[r] - y[r])
grad[1] = 2. * np.mean(x[r] * (beta[0] + beta[1] * x[r] - y[r]))
return np.array(grad)
# 计算当前权值下的梯度
def update_beta(beta, alpha, grad):
new_beta = np.array(beta) - alpha * grad
return new_beta
# 更新参数
def rmse(beta, x, y):
squared_err = (beta[0] + beta[1] * x - y) ** 2
res = np.sqrt(np.mean(squared_err))
return res
# 更新rmse
np.random.seed(10)
grad = compute_grad_SGD(beta, x, y)
# 计算当前梯度
loss = rmse(beta, x, y)
beta = update_beta(beta, alpha, grad)
# 更新beta值
loss_new = rmse(beta, x, y)
# 确定结束计算的条件
i = 1
i = 1
while np.abs(loss_new - loss) > tol_L:
beta = update_beta(beta, alpha, grad)
grad = compute_grad_SGD(beta, x, y)
if i % 100 == 0:
loss = loss_new
loss_new = rmse(beta, x, y)
print('Round %s Diff RMSE %s'%(i, abs(loss_new - loss)))
i += 1
print('Coef: %s \nIntercept %s'%(beta[1], beta[0]))
小批量随机梯度下降则是对二者的折中,随机取一部分用于计算梯度,新引入了一个量叫做batch,用于记录应该取多少的数据用于更新梯度,也只需要在全批量梯度下降的基础上改一句代码:
def compute_grad_batch(beta, batch_size, x, y):
grad = [0, 0]
r = np.random.choice(range(len(x)), batch_size, replace=False)
grad[0] = 2. * np.mean(beta[0] + beta[1] * x[r] - y[r])
grad[1] = 2. * np.mean(x[r] * (beta[0] + beta[1] * x[r] - y[r]))
return np.array(grad)
完整代码如下:
# 自变量x为id 因变量y为question
# 回归模型为简单的y=β0+β1x
# 误差函数为均方误差函数
import pandas as pd
import numpy as np
train = pd.read_csv('data/train.csv')
test = pd.read_csv('data/test.csv')
submit = pd.read_csv('data/sample_submit.csv')
# 读取训练集和测试集
# 初始设置
beta = [1, 1]
alpha = 0.2
tol_L = 0.1
batch_size = 16
# 对x进行归一化
max_x = max(train['id'])
x = train['id'] / max_x
y = train['questions']
# 定义计算mini-batch随机梯度的函数
def compute_grad_batch(beta, batch_size, x, y):
grad = [0, 0]
r = np.random.choice(range(len(x)), batch_size, replace=False)
grad[0] = 2. * np.mean(beta[0] + beta[1] * x[r] - y[r])
grad[1] = 2. * np.mean(x[r] * (beta[0] + beta[1] * x[r] - y[r]))
return np.array(grad)
# 定义更新beta的函数
def update_beta(beta, alpha, grad):
new_beta = np.array(beta) - alpha * grad
return new_beta
# 定义计算RMSE的函数
def rmse(beta, x, y):
squared_err = (beta[0] + beta[1] * x - y) ** 2
res = np.sqrt(np.mean(squared_err))
return res
# 进行第一次计算
np.random.seed(10)
grad = compute_grad_batch(beta, batch_size, x, y)
loss = rmse(beta, x, y)
beta = update_beta(beta, alpha, grad)
loss_new = rmse(beta, x, y)
# 开始迭代
i = 1
while np.abs(loss_new - loss) > tol_L:
beta = update_beta(beta, alpha, grad)
grad = compute_grad_batch(beta, batch_size, x, y)
if i % 100 == 0:
loss = loss_new
loss_new = rmse(beta, x, y)
print('Round %s Diff RMSE %s'%(i, abs(loss_new - loss)))
i += 1
print('Coef: %s \nIntercept %s'%(beta[1], beta[0]))
