机器学习算法学习02：决策树的学习以及应用决策树解决Cora数据集论文分类问题

机器学习算法学习02：决策树的学习以及应用决策树解决Cora数据集论文分类问题

1.前言

决策树方法作为非常经典的机器学习方法，曾经一度是作为专家推荐系统的研究方向。在数十年前，那时的部分人工智能学家相信，通过将生活中的事情逐一用逻辑表示，再通过决策树对这些逻辑的回答进行逐一选择，最终可以使得机器分辨所有物体。即使到了现在，决策树系统逐渐退出人工智能应用领域的今天，他的思想还仍然在生活中被应用着。学习并掌握决策树算法对我们来说依旧十分重要。本次实验代码已发布在GITHUB上，需要的可以上GIT自取：liujiawen-jpg/Decision-Tree: Machine Learn 02 (github.com)

2.算法分析

2.1算法概述

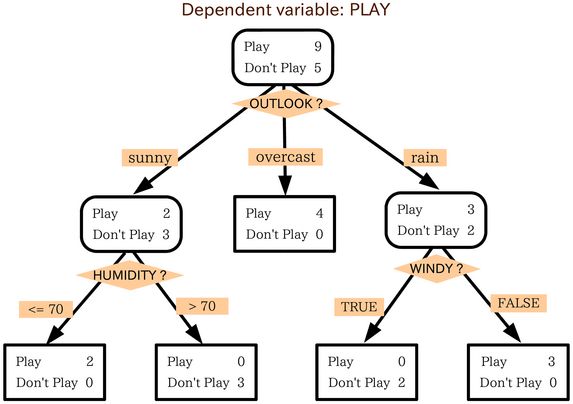
决策树算法其实用逻辑可以非常简单的解释，就是我们将生活中的问题转化为一个个逻辑问题，我们用下面这张图来进行解释：

如上图，我们想要决定今天到底要不要出去外面玩。那么有时候外面天气可能下雨刮风 或者说非常炎热，我们可能只想窝在家里打游戏，决策树模拟了我们这种决策树过程。我们以最左边的叶子节点来叙述。首先我们要查看外面的天气景色（outlook）属性，发现是晴天，接下来我们判断湿度是否大于七十，如果大于，很可惜又热又湿的天气并不适合我出去玩，只能在家里玩游戏了。但是如果小于七十，那么今天是一个不可多得的好天气，我们应该出去玩。

通过上面这个案例，我们得知了决策树算法的大致流程，是不是觉得他看起来并不是很难。好像过于抽象到连数学公式都很难描述他。但这里其实有一个很重要的因素，那么就是为什么outLook（这里我们称之为决策属性）的决策优先级要排在humidity（湿度）,windy（刮风的）之前。在这个简单的例子之前我们还能判断他的优先级，但是进入一些足够复杂，决策属性足够多的问题时，我们是否还能主观判断谁应该作为优先级，所以选择决策属性的优先级也变得极为重要（如何判断优先级，我们留到后面再说）。那么到这里决策树的算法步骤相信大家就看得出来了：

1. 选择数据集中各个决策属性的优先级

2. 通过各个决策属性各个优先级，训练集的数据和标签用于生成决策树（这里可以认为是在训练步骤）

3. 将测试集输入决策树，通过各个决策树的属性比较，最终由遍历到的叶子节点的标签作为测试结果的标签

2.2 算法优化

看似上面的步骤，已经十分完美了，但这里还需要注意一个问题，如果最终测试数据遍历下去找到的叶子节点为空怎么办（即没有对应的叶子节点）。为什么会出现这样的结果呢？这是很正常的，首先我们需要知道，我们决策树全部都是基于我们的训练数据来生成的，我们仍然用上面的决策树进行举例：

如果我们的训练集中没有出现Humidity(湿度)<=70的时候，即生成的决策树中不存在最左边的叶子节点的时候，但我们测试的时候遇到了这种结果我们应该如何解决？我们的算法应该返回什么结果 ，总不能返回对不起无查询结果而返回吧。这个时候前人提出了一个改进方法，当查询到的叶子节点为空时。算法统计该空节点的兄弟节点中出现最多的类别作为我们返回的类别。

比如上图这种出现情况最左边的叶子节点为空的时候，我们统计他的兄弟节点发现只有一个节点他的类别是不出去玩，那么我们就放心地选择不出去玩算了（虽然你发现这样的结果和真实相悖，但没办法训练集如果没有办法包括所有情况的话，我们只能使用类似投票表决的方法来决定了）。那么改良后的步骤就调整为这样：

1. 选择数据集中各个决策属性的优先级
2. 通过各个决策属性各个优先级，训练集的数据和标签用于生成决策树（这里可以认为是在训练步骤）
3. 将测试集输入决策树，通过各个决策树的属性比较，最终由遍历到的叶子节点的标签作为测试数据的结果，如果遍历到的叶子节点为空，则统计该空节点的兄弟节点中出现次数最多的标签，作为测试数据的输出结果。

那么到这里算法陈述完了，接下来我们需要使用代码对于上述算法的实现。

3.算法代码

3.1 决策属性优先级选择

在之前，我们说过一个数据拥有非常多的属性，选择各个属性在决策树节点中的优先级变得尤为重要，但是到底用什么标准去划分，用什么公式去划分显得尤为重要，这里我使用了三种方法用于进行数据集的划分：

3.1.1 信息熵

信息熵是由信息论之父香农提出的，他认为数据的混乱程度是可以进行量化的，于是提出了信息熵的概念，对于数据U我们对的信息熵定义如下：
$H(U)=E\left[-\log p_i\right]=-{\sum }_{i=1}^n{p}_i\log p_i$

这里做出解释，n为数据中的类别，$p_i$为i类别出现的概率，$log{p}_i$为以2为底数$p_i$为真值的结果，对每个类我们计算这两种结果，并将求他们的乘积之和作为该数据集的信息熵，信息熵代表数据集的混乱程度。下面我们编写代码来将该公式来实现：

#计算信息熵
def calcShannonEnt(dataSet, method = 'none'):
    numEntries = len(dataSet)
    labelCount = {
     }
    for feature in dataSet:
        if method =='prob': #统计信息增益率时使用
            label =  feature
        else:
            label = feature[-1] #输入信息默认最后一维为标签
        if label not in labelCount.keys():
            labelCount[label]=1
        else:
            labelCount[label]+=1
    shannonEnt = 0.0
    for key in labelCount:
        numLabels = labelCount[key]
        prob = numLabels/numEntries
        shannonEnt -= prob*(log(prob,2))
    return shannonEnt

通过上述代码，我们便可以将一个数据集的信息熵计算出来，那么回到我们原来的问题上，我们如何通过计算信息熵来确定决策属性的优先级呢？这里我们还需要一个信息增益增益：
$$\mathrm{Gain}(D,a)=\mathrm{Ent}(D)-\sum _{v=1}^V\frac{\left|D^v\right|}{|D|}\mathrm{Ent}\left(D^v\right)$$
也就是对每个可以用来决策的属性，我们都用它划分数据集后并计算划分后的信息熵，然后用总的数据集的信息熵减去该信息熵，这我们称之为该属性的信息增益。可以发现当该属性划分后的数据集的混乱程度越低（也就是说使用他划分后效果好），信息熵越低，则它所带来的的信息增益也会越大。所以我们遍历所有决策属性计算他们的信息增益，选取信息增益的大小作为我们划分数据属性的优先级：

#使用决策属性划分数据集，会将数据集axis维度的值等于value的值的数据集切出来
def splitDataSet(dataSet, axis, value): #划分数据集
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            # 去掉对应位置的特征
            retDataSet.append(reducedFeatVec)
    return retDataSet

#选择最佳划分数据集的属性
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) -1 #最后一个位置的特征不算
    baseEntropy = calcShannonEnt(dataSet) #计算数据集的总信息熵
    bestInfoGain = 0.0
    bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        for value in uniqueVals:
            # 通过不同的特征值划分数据子集
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob *calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy #计算每个信息值的信息增益
        if(infoGain > bestInfoGain): #信息增益最大的作为
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature #返回信息增益的最佳索引

3.2.2 信息增益率

但是信息增益其实是有偏向性的，他十分偏向于拥有更多选择的决策属性（如果我们将数据编号拿来也作为决策属性毫无疑问他将作为第一优先级的决策属性）这也导致了部分情况下决策树正确率受到了影响，那么学者又提出了一个新的数据划分方法–信息增益率（Gain ratio）。也就是是在原有信息增益的情况下我们多考虑一个对于属性内部也计算一次信息熵：
$$\mathrm{Gain}\mathrm{ratio}(D,a)=\frac{\mathrm{Gain}(D,a)}{\mathrm{IV}(a)}$$

$$\mathrm{I}\mathrm{V}(a)=-\sum _{v=1}^V\frac{\left|D^v\right|}{|D|}{\log }_2\frac{\left|D^v\right|}{|D|}$$

也就是说，我们也需要对内部再次进行一次划分并用类似信息熵的方式来求IV(a)：

def calcShannonEnt(dataSet, method = 'none'):
    numEntries = len(dataSet)
    labelCount = {
     }
    for feature in dataSet:
        if method =='prob': #当参数为prob时转而计算信息增益率
            label =  feature
        else:
            label = feature[-1]
        if label not in labelCount.keys():
            labelCount[label]=1
        else:
            labelCount[label]+=1
    shannonEnt = 0.0
    for key in labelCount:
        numLabels = labelCount[key]
        prob = numLabels/numEntries
        shannonEnt -= prob*(log(prob,2))
    return shannonEnt

def chooseBestFeatureToSplit3(dataSet): #使用信息增益率进行划分数据集
    numFeatures = len(dataSet[0]) -1 #最后一个位置的特征不算
    baseEntropy = calcShannonEnt(dataSet) #计算数据集的总信息熵
    bestInfoGain = 0.0
    bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        newEntropyProb = calcShannonEnt(featList, method='prob') #计算内部信息增益率
        uniqueVals = set(featList)
        newEntropy = 0.0
        for value in uniqueVals:
            # 通过不同的特征值划分数据子集
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob *calcGini(subDataSet)
        newEntropy  = newEntropy/newEntropyProb
        infoGain = baseEntropy - newEntropy #计算每个信息值的信息增益
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature #返回信息增益的最佳索引

3.3.3 基尼系数

基尼系数，相信大家并不陌生，各个新闻中也经常出现。它经常被用于衡量国家的贫富差距，在CART决策树中，作者采用他来作为决策属性划分的依据。在这里就让我们揭开他的神秘面纱，一起来看看他具体是如何计算的，对于数据集D我们定义基尼系数如下：
$$\begin{array}{rl}\mathrm{Gini}(D)& =\sum _{k=1}^{|\mathcal{Y}|}\sum _{k^{\prime }\ne k}{p}_k{p}_{k^{\prime }}\\ & =1-\sum _{k=1}^{|\mathcal{Y}|}{p}_k^2\end{array}$$
$p_k$代表第数据集为K个类别的概率，也就是求数据集中某个决策属性出现的所有类别概率的平方和，最后与1作差获得结果。那么如何对于们每个决策属性我们还需要再计算一个关于他们的基尼指数，如对于属性a,我们计算他的基尼指数：
$$Ginindex(D,a)=\sum _{v=1}^V\frac{\left|D^v\right|}{|D|}\mathrm{Gini}\left(D^v\right)$$
也就会我们还需要计算每个条件占所有数据集的概率并与之相乘,同时在书写代码有一个注意事项就是，基尼指数越小代表数据集差异越大，所以区别于之前的选择标准，这里我们认为数据集越小越符合选择标准：

def calcGini(dataset):
    feature = [example[-1] for example in dataset]
    uniqueFeat = set(feature)
    sumProb =0.0
    for feat in uniqueFeat:
        prob = feature.count(feat)/len(uniqueFeat)
        sumProb += prob*prob
    sumProb = 1-sumProb
    return sumProb
def chooseBestFeatureToSplit2(dataSet): #使用基尼系数进行划分数据集
    numFeatures = len(dataSet[0]) -1 #最后一个位置的特征不算
    bestInfoGain = 0.0
    bestFeature = np.Inf
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        for value in uniqueVals:
            # 通过不同的特征值划分数据子集
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob *calcGini(subDataSet)
        infoGain = newEntropy 
        if(infoGain < bestInfoGain): # 选择最小的基尼系数作为划分依据
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature #返回决策属性的最佳索引

3.2 数据集的预处理

在此次我们数据集选择的是著名的图神经网络分类数据集Cora论文分类数据集（关于他的详细介绍可以查看我的博客(5条消息) 图神经网络学习01：图卷积神经网络GCN实战解决论文分类问题(tensorflow实现)_theworld666的博客-CSDN博客），该数据集收集了六个学术方向的2708篇论文，利用1433个关键词对他进行编码，大概意思就是假设是神经网络方向相关论文，那么学习率，神经网络，模型，这些词应该会出现得比较频繁，反过来我们也可以认为当出现这些词时这篇论文大概率是神经网络方向的学术论文。我们可以先解析一下他的数据：

import pandas as pd
import numpy as np
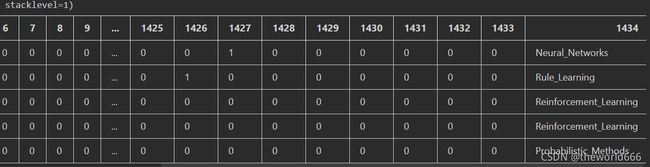
data=pd.read_csv('cora/cora.content',sep = '\t',header=None) #读取数据查看
data.head() #查看数据前五项

该数据集利用1433个关键词对论文进行编码，该关键词出现就是1，没出现就是0，同时给每个论文贴上他们属于什么学术方向的标签，这里我们可以利用pandas的方法查看一下到底每个标签的数量如何：

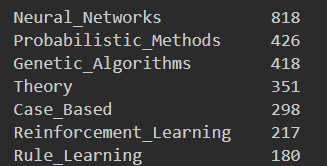
feature=data.iloc[:,-1]
feature.value_counts()

可以看到有七类其中关于神经网络的学术论文最多，达到了818个(可见火热)，这就是我们希望决策树最终输出的真值。那么接下来我们需要先处理一下数据集，这里由于我使用的决策树算法代码的数据输入形式，我将整个数据转换为列表的形式：

def load_Cora():
    dataSet=pd.read_csv('cora/cora.content',sep = '\t',header=None)
    feature = dataSet.iloc[:,1:] #第一列是论文编号，我们不需要所以截取第一列之后的数据
    feature = np.array(feature)
    dataList = feature.tolist() #先转换成向量再转换为列表
    label = [i for i in range(len(dataList[0])-1)] # 这里的标签是用于索引属性使用的
    return dataList,label

通过以上的步骤我们完成了构建决策树的准备步骤：

• 编写数据划分代码，选择决策属性方法代码
• 完成了数据预处理

接下来，我们开始进入决策树代码的核心重点–如何通过训练数据生成我们的决策树

3.3 决策树的生成

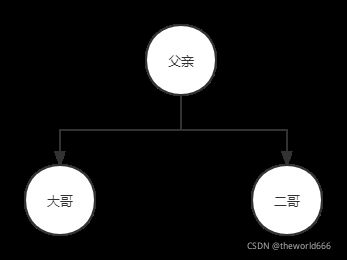
虽然名字是决策树，看起来像是依靠需要树形结构来构造的。但实际上我们为了更方便的取出数据同时也是因为可能出现两个以上子节点的情况，这里我们不使用树形结构表达决策树，我们使用字典结构来存储决策树。那么如何使用字典结构来表达一个树形结构呢？这里我们用一个例子来阐述如下图：

那么我们可以将根节点付清作为key 创建一个这样的字典{父亲：{左：大哥，右：二哥}}，如果二哥也有自己的子节点，我们也可以按照这个样子继续嵌套字典，从而来表达一个树形结构。于是我们编写创建决策树代码如下

def createTree(dataSet, labels):
    classList = [example[-1] for example in dataSet]
    # 获取数据集的对应标签序列
    if classList.count(classList[0]) == len(classList):
        return classList[0] # 当所有特征的类别都相同时停止划分
    if len(dataSet[0]) == 1: #当遍历完是所有特征的时候返回出现次数最多的类别
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)#选择最容易划分的数据集
    bestFeatLabel = labels[bestFeat]
    myTree = {
     bestFeatLabel:{
     }}
    del(labels[bestFeat]) # 删除对应位置的标签
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues) #获取该列特征值的所有不同的特征值
    for value in uniqueVals: #利用该列的特征值来创造树
        subLabels = labels[:] #拷贝整个标签
        #递归构造字典
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
    return myTree

这里需要注意一件事，就是按照上面的代码我们生成的决策树字典数据他的生命周期是维持到程序结束为止的，也就是下次我们还需要重新构造。但当决策属性过多，比如本次使用数据集1433个决策属性，我们每个属性取值为0,1。那么我们的数据的大小就有将近2的1400次方左右这实在是太大了。所以为了数据集重复利用,我们还需要对数据进行存储以及导入：

import pickle
def storeTree(inputTree,filename):
    with open(filename,'wb') as f: #将数据集使用二进制存储
        pickle.dump(inputTree,f)
def reloadTree(filename):
    fr = open(filename, 'rb')#读取时也需要使用二进制方式
    return pickle.load(fr)

3.4 决策树的分类

至此我们已经创造了决策树结构，那么如何使用这个节点进行分类，以及如何使用我们之前提到的当查找到的节点为空该如何处理的步骤呢，让我们继续往下看：

#运用决策树进行分类
def classify(inputTrees, featLabels, testVec):
    firstStr = list(inputTrees.keys())[0]
    secondDict = inputTrees[firstStr]
    featIndex = featLabels.index(firstStr) #寻找决策属性在输入向量中的位置
    classLabel = -1 #-1是作为flag值
    for key in secondDict.keys():
        if testVec[featIndex] == key: #如果对应位置的值与键值相等
            if type(secondDict[key]).__name__ == 'dict':
                #继续递归查找
                classLabel = classify(secondDict[key],featLabels, testVec)
            else:
                classLabel = secondDict[key] #查找到子节点则返回子节点的标签
    #标记classLabel为-1当循环过后若仍然为-1，表示未找到该数据对应的节点则我们返回他兄弟节点出现次数最多的类别
    return getLeafBestCls(inputTrees) if classLabel == -1 else classLabel 

#求该节点下所有叶子节点的列表
def getLeafscls(myTree, clsList):
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            clsList =getLeafscls(secondDict[key],clsList)
        else:
            clsList.append(secondDict[key])
    return clsList

#返回出现次数最多的类别
def getLeafBestCls(myTree):
    clsList = []
    resultList = getLeafscls(myTree,clsList)
    return max(resultList,key = resultList.count)

4.算法运行与评估

完成了以上代码的书写我们就编写运行程序将这上面的代码整合起来：

from tree import *
from treePlotter import * #这个是用于可视化的代码库
import pandas as pd
import numpy as np
import sys


if __name__ == '__main__':
    np.random.seed(1) #固定种子使得每次打乱的结果都一致，方便控制变量用于测试
    dataSet,label = load_Cora() #导入数据集
    train_num = int(len(dataSet)*0.8) #使用百分之八十得到数据进行训练，百分之二十数据验证
    train_data = dataSet[:train_num]
    test_data = dataSet[train_num+1:]
    trainTree = createTree(train_data,label) #利用数据集标签创建二叉树
    storeTree(trainTree,'CORATree.txt') #将决策树存储进入TXT文件
    # trainTree = reloadTree('CORATree.txt') #导入存储好的树
    createPlot(trainTree)#绘画二叉树
    test_labels = [i for i in range(1433)] 
    errCount = 0.0
    for data in test_data:
        testVec = data[:-1]
        result = classify(trainTree,test_labels, testVec) #获得分类结果
        if result!=data[-1]: #统计错误个数
            errCount+=1.0
    prob = (1-(errCount/len(test_data)))*100 #计算准确率
    print(prob)

这里我们还可以查看一下可视化代码，可以发现决策属性（足足有1433个决策属性）过多也导致了最终枝条过多，图的可视化效果不是很好。

在评估算法正确率的时候，需要阐明我是怎么判断算法到底对模型有没有用。比如一个二分类问题，你说算法正确率达到百分之52左右，那么就说明你这个算法基本没用，因为我瞎猜二分类正确率也在百分之五十左右。反之如果是六分类，七分类问题你达到百分之五十。就说明你的算法的确发挥了一定作用，因为这正确率远比瞎猜高（），这次数据集共有七个分类，所以我们正确率达到百分之五十其实已经证明算法的准确了。

4.1 使用信息增益来划分数据集

当使用信息增益时，决策树如下：

正确率更稳定在64.95

4.2 使用信息增益率划分数据

决策树如下：

正确率稳定在 49.95左右

4.3 使用基尼指数划分数据

可视化决策树如下：

准确率稳定在67左右。

通过以上三种算法比较，我们发现，基尼指数划分数据集的准确率最高百分之六十七左右，反而是信息增益率改良后的决策树准确率最低只有49左右（可能是因为此次所有决策属性的值只有0和1，所有信息增益率其实并不适用）。但整体准确率其实较低，这说明决策树其实不太适合决策属性过多的条件下。

5.结语

通过此次决策树的学习和代码的运行，我掌握了决策树基础算法的逻辑，和如何解析数据使得数据符合决策树算法输入。决策树的算法不需要调整过多的参数，同时算法的可解释性也非常的强。但决策树的缺点也同样在此次实验中暴露出来了，当决策属性过多，整个决策树的算法的开销将会膨胀到非常大。同时这样扩展出来的数据集也容易达到过拟合的状态。于是学者之后还研发出来了预剪枝，和后剪枝等技术，以及使用随机森林算法来解决这些相关问题。