kmeans聚类算法_客户细分——K-Means聚类

RFM模型多用于已知目标数据集，场景具有一定的局限性，本篇运用一个适用比较广泛的聚类算法——K-Means，它属于无监督机器学习，K-Means算法的思想很简单，对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇，让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大。

本文还是用实例数据进行讲述。

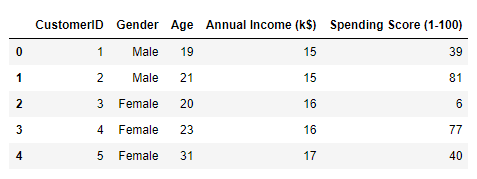
数据背景：数据为某商场会员基本信息，包括CustomerID（客户ID），Gender（性别），Age（年龄），Annual Income (k$)（年收入）和Spending Score (1-100)（消费得分：根据顾客消费行为，例如客户行为和购买数据商场的评分），通过已有信息对客户进行细化分类，以便营销运营团队更好的制定策略。

数据集地址：

https://www.kaggle.com/vjchoudhary7/customer-segmentation-tutorial-in-python​www.kaggle.com

一、数据处理

#导入数据分析需要的包
import pandas as pd
import numpy as np
#可视化包
import seaborn as sns
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
%matplotlib inline
#忽略警告信息
import warnings
warnings.filterwarnings('ignore')
#读取数据
df=pd.read_csv('C:/Users/dwhyx/Downloads/data/Mall_Customers.csv')
df.head()

#查看缺失值
df.isnull().any()

经查询，本数据集不存在缺失值，数据表结构也比较简单，原数据不需要进行过多处理。

二、数据可视化分析

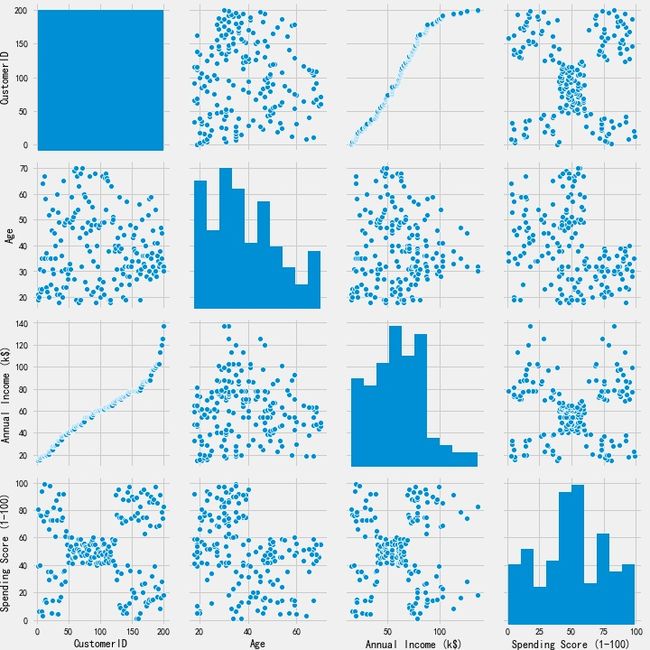
2.1预览数据分布

sns

2.2不同性别在各变量之间的关系

从上图中，大体能看出每个变量之间相关分布，加入性别变量，查看不同性别在各变量之间是否有区别。

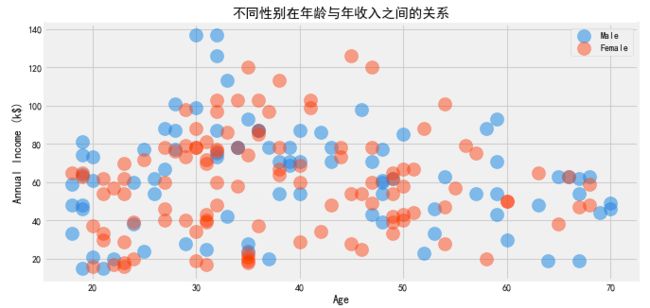
#不同性别在年龄与年收入之间的关系
plt.figure(1,figsize=(10,5))
for gender in ['Male','Female']:  
    plt.scatter(x='Age',y='Annual Income (k$)',data=df[df['Gender']==gender],
               s=200,alpha=0.5,label=gender)
plt.xlabel('Age'),plt.ylabel('Annual Income (k$)') 
plt.title('不同性别在年龄与年收入之间的关系')
plt.legend() 
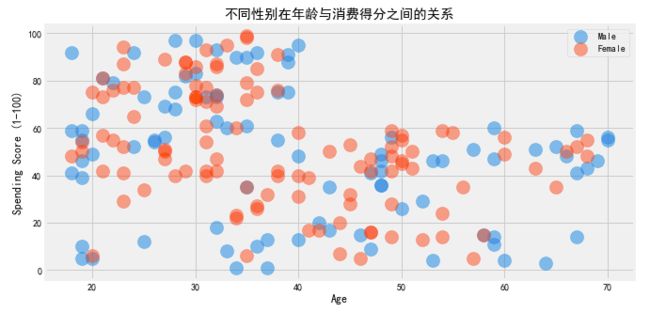
plt.show()

#不同性别在年龄与年收入之间的关系
plt.figure(1,figsize=(10,5))
for gender in ['Male','Female']:  
    plt.scatter(x='Age',y='Spending Score (1-100)',data=df[df['Gender']==gender],
               s=200,alpha=0.5,label=gender)
plt.xlabel('Age'),plt.ylabel('Spending Score (1-100)') 
plt.title('不同性别在年龄与消费得分之间的关系')
plt.legend() 
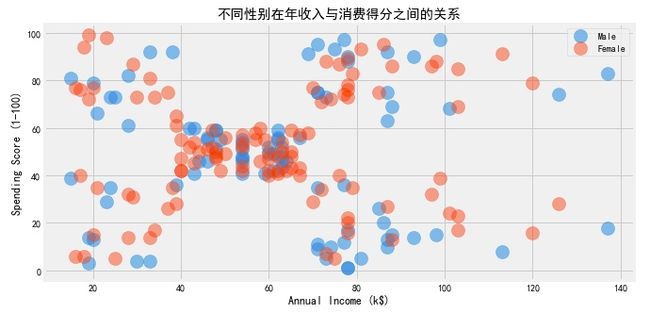
plt.show()

#不同性别在年收入与消费得分之间的关系
plt.figure(1,figsize=(10,5))
for gender in ['Male','Female']:  
    plt.scatter(x='Annual Income (k$)',y='Spending Score (1-100)',data=df[df['Gender']==gender],
               s=200,alpha=0.5,label=gender)
plt.xlabel('Annual Income (k$)'),plt.ylabel('Spending Score (1-100)') 
plt.title('不同性别在年收入与消费得分之间的关系')
plt.legend() 
plt.show()

三、K-Means聚类分析

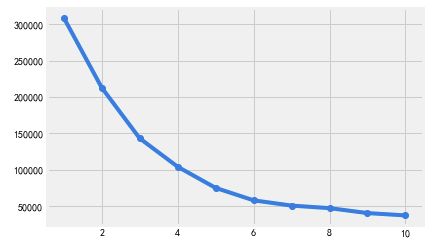
3.1寻找最佳聚类个数——The Elbow Method手肘法则

#选取字段
df1=df[['Age' , 'Annual Income (k$)' ,'Spending Score (1-100)']].iloc[: , :].values
#导入包
from sklearn.cluster import KMeans
inertia=[]
for i in range(1,11):  
    km=KMeans(n_clusters=i,init='k-means++',max_iter=300,n_init=10,random_state=0)
    km.fit(df1)
    inertia.append(km.inertia_)
plt.plot(range(1,11),inertia,'o-')

利用手肘法，通过图形发现，拐点在6这个位置，即最佳聚类个数为6。

3.2降维

cluster = KMeans(n_clusters=6)  #设定族数为6
cluster.fit(df1)

from sklearn import manifold 
tsne = manifold.TSNE()   #将关系数据降维二维
tsne_data = tsne.fit_transform(df1)
tsne_df = pd.DataFrame(tsne_data,columns=['col1','col2'])
tsne_df.loc[:,'label']=cluster.predict(df1)
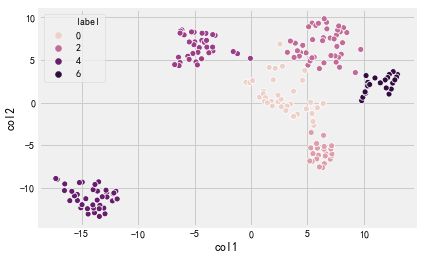
sns.scatterplot(x = 'col1',y='col2',hue='label',data=tsne_df)

通过降维，将三维立体图降维为平面图，上图6个不同颜色代表6个不同的人群，因为K-Means是无监督学习，主要负责把特征比较明显的用户归为一类，具体每一类分别代表什么群体，需要我们自己进行分析，下面会有讲述。

3.3评估聚类结果

from sklearn import metrics
score = metrics.silhouette_score(df1,tsne_df.loc[:,'label'])
print('聚类个数为6时，轮廓函数:' , score)

轮廓函数为：0.45，聚类效果较好。

PS：轮廓系数取值为[-1, 1]，其值越大越好，且当值为负时，表明样本被分配到错误的簇中，聚类结果不可接受。对于接近0的结果，则表明聚类结果有重叠的情况。

3.4聚类人群分析

cluster_centers=cluster.cluster_centers_
result = pd.DataFrame(data=cluster_centers,
          columns = ['Age','Annual Income(k$)','Spending Score(1-100)']).reset_index(drop= True)
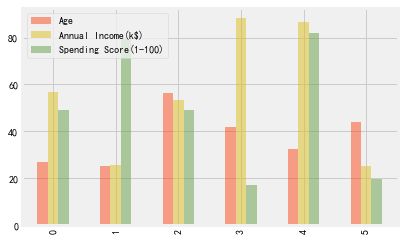
result.plot(kind='bar',color=['C1','C2','C3'],clip_on=False,alpha = 0.5)

• 0组：平均年龄25岁左右，收入60k$左右，消费分50左右（重要发展人群：青年为主，收入和消费得分居中，潜力大）
• 1组：平均年龄25岁左右，收入25k$左右，消费分>80（冲动消费人群：青年为主，收入一般但消费得分较高）
• 2组：平均年龄55岁左右，收入55k$左右，消费分50左右（重要保持人群：中老年为主，收入和消费得分居中）
• 3组：平均年龄40岁左右，收入>80k$，消费分20左右（谨慎消费人群：中年为主，收入很高但消费得分较低）
• 4组：平均年龄30岁左右，收入>80k$，消费分>80（重要价值人群：中年为主，收入和消费得分都很高，属于最优客户群体）
• 5组：平均年龄40岁左右，收入30k$左右，消费分20左右（一般价值人群：中年为主，收入和消费得分都较低）

#把得到的聚类标签添加到原数据集
df['cluster'] = cluster.labels_
#查看各类人群各自占比
df['cluster'].value_counts(1)

结果得到，2组（重要保持客户）人数最多，占比22.5%；5组（一般价值客户）人数最少，占比10.5%。

至此我们已经把所有客户细分为6类，针对不同客户特征，可以制定不同的营销运营策略，使运营效果最大化。