如何给普通图片加上水波纹【shader 奇技淫巧】

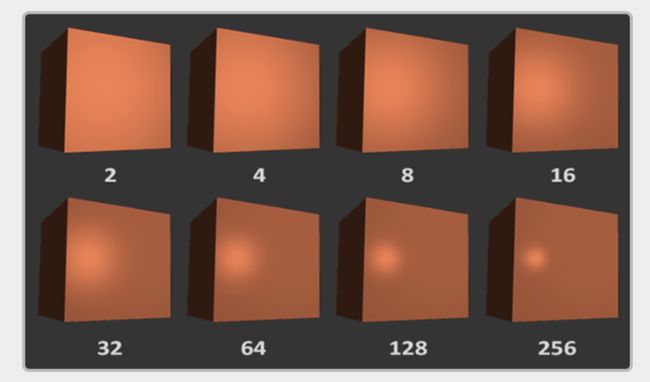
3D场景实现水波纹，我们往往会使用网格去模拟真实的水流动，无论是简单的三角函数或是gerstner wave。然后通过真实物理渲染（base physcal render）来实现其中的折射与反射。这些实现可以参考《GPU GEMS》第一版。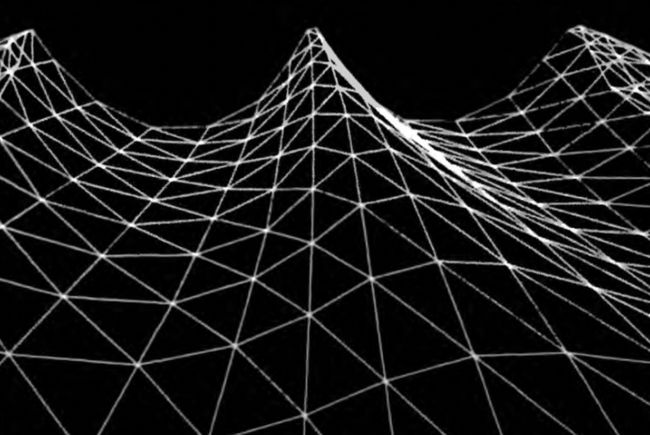

原谅我，古早年代的书就这效果

但对于2D场景这样的模拟就显得开销过大，2D场景往往会使用一些“投机取巧”的方式，例如使用沃罗诺伊纹理（voronoi）来模拟焦散效果。

而本文就来聊聊如何投机出一个2D的水波纹效果，最终效果如下：

最终代码：

precision mediump float;
/* 
 变量申明
*/
varying vec2 uv;
uniform sampler2D u_image0;
uniform float u_time;
uniform float u_offset;
uniform float u_radio;

#define MAX_RADIUS 1
#define DOUBLE_HASH 0
#define HASHSCALE1 .1031
#define HASHSCALE3 vec3 (.1031, .1030, .0973)

/* 
 工具函数
*/
float hash12 (vec2 p) {
  vec3 p3 = fract (vec3 (p.xyx) * HASHSCALE1);
  p3 += dot (p3, p3.yzx + 19.19);
  return fract ((p3.x + p3.y) * p3.z);
}

vec2 hash22 (vec2 p) {
  vec3 p3 = fract (vec3 (p.xyx) * HASHSCALE3);
  p3 += dot (p3, p3.yzx + 19.19);
  return fract ((p3.xx + p3.yz) * p3.zy);

}

void main () {
  vec2 frag = uv;
  frag.x *= u_radio;
  frag = frag * u_offset * 1.5;
  vec2 p0 = floor (frag);
  vec2 circles = vec2 (0.);
  for (int j = -MAX_RADIUS; j <= MAX_RADIUS; ++j) {
    for (int i = -MAX_RADIUS; i <= MAX_RADIUS; ++i) {
      vec2 pi = p0 + vec2 (i, j);
      vec2 hsh = pi;
      vec2 p = pi + hash22(hsh) ;
      // hash12 添加随机
      float t = fract (0.3 * u_time + hash12(hsh));
      vec2 v = p - frag;
      // 半径：
      float d = length (v) - (float (MAX_RADIUS) + 1. )*t  ;
      float h = 1e-3;
      float d1 = d - h;
      float d2 = d + h;
      float p1 = sin (31. * d1) * smoothstep (-0.6, -0.3, d1) * smoothstep (0., -0.3, d1);
      float p2 = sin (31. * d2) * smoothstep (-0.6, -0.3, d2) * smoothstep (0., -0.3, d2);
      circles += 0.5 * normalize (v) * ((p2 - p1) / (2. * h) * (1. - t) * (1. - t));
    }
  }
  // 两轮循环添加了weight个波(取平均)
  float weight = float ((MAX_RADIUS * 2 + 1) * (MAX_RADIUS * 2 + 1));
  circles /= weight;
  float intensity = mix (0.01, 0.05, smoothstep (0.1, 0.6, abs (fract (0.05 * u_time + .5) * 2. - 1.)));
  vec3 n = vec3 (circles, sin ( dot (circles, circles)));
  vec3 colorRipple = texture2D (u_image0, uv + intensity * n.xy).rgb;
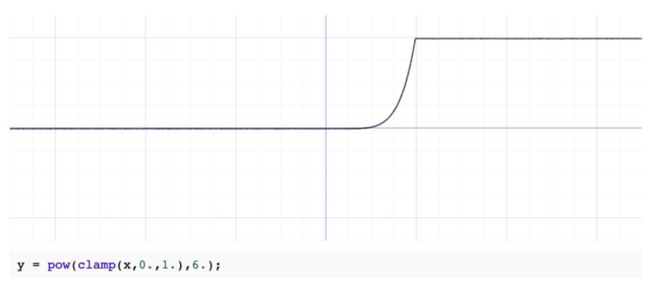
  float colorGloss = 5. * pow (clamp (dot (n, normalize (vec3 (1., 0.7, 0.5))), 0., 1.), 6.);
  vec3 color = colorRipple + vec3(colorGloss);
  gl_FragColor = vec4 (color, 1.0);
}

折射和反射

2D模拟水波纹，主要就是要实现水波的折射与反射。
它们分别由反射项vec3(colorGloss)和折射项colorRipple控制
其中反射项由colorGloss控制

float colorGloss =5.* pow (clamp (dot (n, normalize (vec3(1.,0.7,0.5))),0.,1.),6.);

其中带有一个衰退函数：

这里借用了布林冯反射模型的高光项：

float gloss = pow(max(0,dot(n, viewDir)),_Gloss);

而normalize (vec3(1.,0.7,0.5))则可以类比为布林冯反射模型的指向相机的向量。由于没有3D场景只能虚假地模拟一个，关于这块相关的图形学内容就不展开了，感兴趣的可以阅读LearnOpenGL - Basic Lighting

colorRipple

让我再来看看折射项colorRipple：

vec3 colorRipple = texture2D (u_image0, uv + intensity * n.xy).rgb;

这主要依赖texture2D实现，一般我们使用texture2D(u_image0, uv)来呈现纹理，但也可以使用texture2D(u_image0, uv+offset)来实现一些奇特的效果，例如此前使用在10行代码搞定“热成像”实现的colorRamp，以及实现的几款2077风格的shader赛博朋克效果。
今天则通过offset加上一个与定点有关的距离场实现波动效果，例如：

......
vec2 offset = sin(23.*length(uv-vec2(0.5))-u_time);
vec3 color =  texture2D (u_image0, uv + offset).rgb;
gl_FragColor = vec4 (color, 1.0);
......

值得注意的是这里用到了反射项一样使用了向量n，但只用了向量的方向，而周期性则由intensity实现：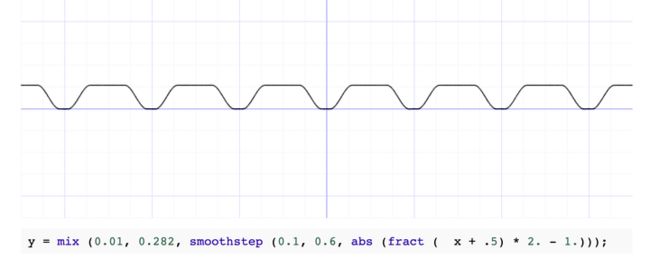

现在让我们来看看如何实现波的叠加

实现叠加

实现一个水波很容易但如何实现波的叠加？最先想到的是通过noise生成随机波源，用framBuffer记录。本文提供了一个不错的思路：
首先使用阶梯函数让画面重复

vec2 frag = uv;
frag *= u_radio;
......
vec3 color = texture2D (u_image0, fract(frag)).rgb;
gl_FragColor = vec4 (color, 1.0);
......

这里有一个小技巧，如果重复的不是uv坐标而是纹理，我们就能让效果重复展示在一个换面中，例如实现一些故障效果：

而本篇我们则需要使用循环来实现多波源效果：

vec2 frag = uv;
frag = frag * 1.5;
vec2 p0 = floor (frag);
vec2 pp = frag - p0;
float offset = 0.03*sin(31.*length(pp)-5.*u_time);
vec3 color =  texture2D (u_image0, uv + normalize(pp)* offset).rgb;
gl_FragColor = vec4 (color, 1.0);

彼此影响

但这样波源直接不会互相影响。此时我们就要通过循环把不同波源的影响累加到同一个向量circles上：

vec2 circles = vec2 (0.);
for (int j = -MAX_RADIUS; j <= MAX_RADIUS; ++j) {
    for (int i = -MAX_RADIUS; i <= MAX_RADIUS; ++i) {
      vec2 pi = p0 + vec2 (i, j);
      vec2 hsh = pi;
      vec2 p = pi ;
      // hash12 添加随机
      float t = fract (0.3 * u_time);
      vec2 v = p - frag;
      // 半径：
      float d = length (v) - (float (MAX_RADIUS) + 1. )*t  ;
      float h = 1e-3;
      float d1 = d - h;
      float d2 = d + h;
      float p1 = sin (31. * d1) * smoothstep (-0.6, -0.3, d1) * smoothstep (0., -0.3, d1);
      float p2 = sin (31. * d2) * smoothstep (-0.6, -0.3, d2) * smoothstep (0., -0.3, d2);
      circles += 0.5 * normalize (v) * ((p2 - p1) / (2. * h) * (1. - t) * (1. - t));
    }
  }

这里MAX_RADIUS=1，所以每一个floor分割的区域不仅接受自己的波源，还同时接受以自己为中心的9宫格另外8个方向的波源。此外这里并没有采用正弦波，而采用了更为逼真的复合波形，加上(1-t)*(1-t)产生的衰减，保证只接受相邻的波不至于穿帮：

如果没有衰减而穿帮，因为波只能传递向相邻的一个单位，无法再继续传播下去：

但这样波就太过规则了，所以通过hash12，hash22两个noise函数给波源加上随机值：

float hash12 (vec2 p) {
  vec3 p3 = fract (vec3 (p.xyx) * HASHSCALE1);
  p3 += dot (p3, p3.yzx + 19.19);
  return fract ((p3.x + p3.y) * p3.z);
}

vec2 hash22 (vec2 p) {
  vec3 p3 = fract (vec3 (p.xyx) * HASHSCALE3);
  p3 += dot (p3, p3.yzx + 19.19);
  return fract ((p3.xx + p3.yz) * p3.zy);

}
......
vec2 pi = p0 + vec2 (i, j);
vec2 hsh = pi;
vec2 p = pi + hash22(hsh) ;
// hash12 添加随机
float t = fract (0.3 * u_time + hash12(hsh));
......

最后选择一种波形：

由于是for循环叠加的circles，所以最后要对它进行平均

// 两轮循环添加了weight个波(取平均)
float weight = float ((MAX_RADIUS * 2 + 1) * (MAX_RADIUS * 2 + 1));
circles /= weight;

最终模拟一个向量n，参与上文的反射项方程，所以我们需要选择一个波形，我这里选择sin（xx + yy）。不过这是模拟，各位看客也可以选择自己喜欢的波形：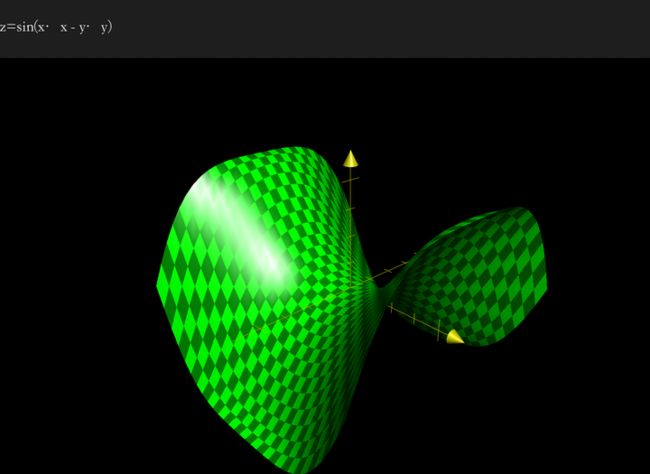

本篇就结束了，下一篇我们来说说，上文中提到的glitch效果要如何制作：