维特比算法（Viterbi）及python实现样例

维特比算法（Viterbi）

维特比算法

维特比算法shiyizhong 动态规划算法用于最可能产生观测时间序列的-维特比路径-隐含状态序列，特别是在马尔可夫信息源上下文和隐马尔科夫模型中。术语“维特比路径”和“维特比算法”也被用于寻找观察结果最有可能解释的相关dongtai 规划算法。例如在统计句法分析中动态规划可以被用于发现最有可能的上下文无关的派生的字符串，有时被称为“维特比分析”。

利用动态规划寻找最短路径

动态规划是运筹学的一个分支，是求解决策过程最优化的数学方法，通常情况下应用于最优化的问题，这类问题一般有很多可行的解，每个解有一个值，而我们希望从中找到最优的答案。

在计算机科学领域，应用动态规划的思想解决的最基本的一个问题就是：寻找有向无环图（篱笆网络）当中两个点之间的最短路径（实际应用于地图导航、语音识别、分词、机器翻译等等）

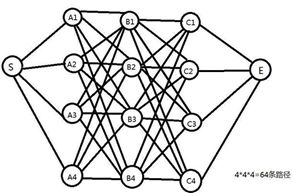
下面举一个比较简单的例子做说明：求S到E的最短路径，如下图（各点之间距离不相同）：

 

 

我们知道，要找到S到E之间最短路径，最容易想到的方法就是穷举法。也就是把所有可能的路径都例举出来。从S走向A层共有4种走法，从A层走向B层又有4种走法，从B层走向C层又有4种走法，然后C层走向E点只有一种选择。所以最终我们穷举出了4*4*4=64种可能。显然，这种方法必定可行，但在实际的应用当中，对于数量及其庞大的节点数和边数的图，其计算复杂度也将会变得非常大，而计算效率也会随之降低。

 

 

因此，这里选择适用一种基于动态规划的方式来寻找最佳路径。

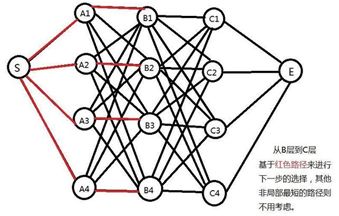
所谓动态规划。其核心就是“动态”的概念，把大的问题细分为多个小的问题，基于每一步的结果再去寻找下一步的策略，通过每一步走过之后的局部最优去寻找全局最优，这样解释比较抽象，下面直接用回刚刚的例子说明。如下图：

 

 

首先，我们假设S到E之间存在一条最短路径（红色），且这条路径经过C2点，那么我们便一定能够确定从S到C2的64条（4*4*4=64）子路经当中，该子路经一定最短。（证明：反证法。如果S到C2之间存在一条更短的子路经，那么便可以用它来替代原先的路径，而原来的路径显然就不是最短了，这与原假设自相矛盾）。

同理，我们也可以得出从S到B2点为两点间最短子路经的结论。这时候，真相便慢慢浮出水面：既然如此，我们计算从S点出发到点C2的最短路径，是不是只要考虑从S出发到B层所有节点的最短路径就可以了？答案是肯定的！因为，从S到E的“全局最短”路径必定经过这些“局部最短”子路经。没错！这就是上面提及到的通过局部最优的最优去寻找全局最优，问题的规模被不断缩小！

接下来，要揭晓答案了！继续看下图：

 

 

回顾之前的分析：我们计算从S到C2点的最短路径时候只需要考虑从S出发到B层所有节点的最短路径，B层也是。对B2来说，一共有4条路线可达，分别是A1->B2,A2->B2,A3->B2, A4->B2。我们需要做的就是A2->B2这条路线保留，而其他3条删掉（因为根据以上的分析，他们不可能构成全程的最短路线）。Ok，来到这里，我们会发现一个和小“漏洞”，这段S->A2->B2->C2->E的路线只是我一厢情愿的假设，最短路径下不一定是经过以上这些点。所以，我们要把每层的每个节点都考虑进来。

以下是具体做法：

step1：从点S出发。对于第一层的4个节点，算出他们的距离d(S,A1),d(S,A2),d(S,A3),d(S,A4),因为只有一步，所以这些距离都是S到它们各自的最短距离

step2:对于B层的所有节点(B1,B2,B3,B4),要计算出S到他们的最短距离。我们知道，对于特定的节点B2，从S到它的路径可以经过A层的任何一个节点(A1,A2,A3,A4)。对应的路径长就是d(S,B2)=d(S,Ai)+d(Ai,B2)（其中i=1，2，3，4）。由于A层有4个节点（即i有4个取值），我们要一一计算，然后找到最小值。这样，对于B层的每个节点，都需要进行4次运算，而B层有4个节点，所以共有4*4=16次运算。

step3:这一步是该算法的核心。我们从step2计算得出的阶段结果只保留4个最短路径值（每个节点保留一个）。那么，若从B层走向C层来说，该步骤的级数已经不再是4*4，而是变成4！也就是说，从B层到C层的最短路径只需要基于B层得出的4个结果来计算。这种方法一直持续到最后一个状态，每一步计算的复杂度为相邻两层的计算复杂度为4*4乘积的正比！再通俗点说，连接着两两相邻层的计算符合变成了“+”号，取代了原先的“*”号。用这种方法，只需要进行4*4*2=32次计算！

其实上述的算法就是著名的维特比算法，事实上非常简单！

若假设整个网格的宽度为D，网格长度为N，那么弱适用穷举法整个最短路径的算法复杂度为O(D^N),而适用这种算法的计算复杂度为O（ND^2）.试想一下，弱D与N都非常大，适用维特比算法的效率将会提高几个数量级！

 

 

 

尝试用高中知识去理解一下Veterbi算法

1、  题目背景

从前有个村儿，村里的人身体情况只有两种可能：健康或者发烧

假设这个村儿的人没有体温计或者百度这种神奇的东西，它唯一判断身体情况的途径是到村头小诊所询问

月儿通过询问村民的感觉，判断他的病情，再假设村民只会回答正常、头晕或冷

有一天村里的澳巴卢就去月儿那询问了

第一天他告诉月儿他感觉正常

第二天他告诉月儿他有点冷

第三天他告诉月儿感觉有点头晕

那么问题来了，月儿如何根据阿鲁的描述情况，推断出这三天中阿鲁的一个身体状态呢？

为此月儿上百度搜google，一番狂搜，发现维特比算法正好能解决这个问题，月儿乐了

2、  已知情况

隐含的身体状况={健康，发烧}

可观察的感觉状态={正常、冷、头晕}

月儿预判的阿鲁的身体状态的概率分布={健康：0.6，发烧：0.4}

月儿认为的阿鲁的身体健康的转换概率分布={

健康->健康：0.7

健康->发烧：0.3

发烧->健康：0.4

发烧->发烧：0.6

}

月儿认为的在相应的健康状况条件下，阿鲁的感觉的概率分布={

健康，正常：0.5，冷：0.4，头晕：0.1；

发烧，正常：0.1，冷：0.3，头晕：0.6

}

阿鲁连续三天的身体感觉依次是：正常、冷、头晕。

3、  已知上述，求：阿鲁这三天的身体健康状态变换的过程是怎么样的？

4、  过程：

根据Viterbi理论，后一天的状态会依赖前一天的状态和当前的可能观察的状态。那么只要根据第一天的正常状态依次推算找出到达第三天头晕状态的最大概率，就可以知道这三天的身体变换情况。

1.初始情况：

P(健康) = 0.6，P(发烧)=0.4。

2.求第一天的身体情况：

计算在阿驴感觉正常的情况下最可能的身体状态。

 

P(今天健康) = P(正常|健康)*P(健康|初始情况) = 0.5 * 0.6 = 0.3

P(今天发烧) = P(正常|发烧)*P(发烧|初始情况) = 0.1 * 0.4 = 0.04

那么就可以认为第一天最可能的身体状态是：健康。

3.求第二天的身体状况：

计算在阿驴感觉冷的情况下最可能的身体状态。

那么第二天有四种情况，由于第一天的发烧或者健康转换到第二天的发烧或者健康。

 

P(前一天发烧，今天发烧) = P(前一天发烧)*P(发烧->发烧)*P(冷|发烧) = 0.04 * 0.6 * 0.3 = 0.0072

P(前一天发烧，今天健康) = P(前一天发烧)*P(发烧->健康)*P(冷|健康) = 0.04 * 0.4 * 0.4 = 0.0064

P(前一天健康，今天健康) = P(前一天健康)*P(健康->健康)*P(冷|健康) = 0.3 * 0.7 * 0.4 = 0.084

P(前一天健康，今天发烧) = P(前一天健康)*P(健康->发烧)*P(冷|发烧) = 0.3 * 0.3 *.03 = 0.027

那么可以认为，第二天最可能的状态是：健康。

4.求第三天的身体状态：

计算在阿驴感觉头晕的情况下最可能的身体状态。

 

P(前一天发烧，今天发烧) = P(前一天发烧)*P(发烧->发烧)*P(头晕|发烧) = 0.027 * 0.6 * 0.6 = 0.00972

P(前一天发烧，今天健康) = P(前一天发烧)*P(发烧->健康)*P(头晕|健康) = 0.027 * 0.4 * 0.1 = 0.00108

P(前一天健康，今天健康) = P(前一天健康)*P(健康->健康)*P(头晕|健康) = 0.084 * 0.7 * 0.1 = 0.00588

P(前一天健康，今天发烧) = P(前一天健康)*P(健康->发烧)*P(头晕|发烧) = 0.084 * 0.3 *0.6 = 0.01512

那么可以认为：第三天最可能的状态是发烧。

5.结论

 

根据如上计算。这样月儿断定，阿驴这三天身体变化的序列是：健康->健康->发烧。

这个算法大概就是通过已知的可以观察到的序列，和一些已知的状态转换之间的概率情况，通过综合状态之间的转移概率和前一个状态的情况计算出概率最大的状态转换路径，从而推断出隐含状态的序列的情况。

 1 import numpy as np
 2 def viterbi(trainsition_probability,emission_probability,pi,obs_seq):
 3     #转换为矩阵进行运算
 4     trainsition_probability=np.array(trainsition_probability)
 5     emission_probability=np.array(emission_probability)
 6     pi=np.array(pi)
 7     obs_seq = [0, 2, 3]
 8     # 最后返回一个Row*Col的矩阵结果
 9     Row = np.array(trainsition_probability).shape[0]
10     Col = len(obs_seq)
11     #定义要返回的矩阵
12     F=np.zeros((Row,Col))
13     #初始状态
14     F[:,0]=pi*np.transpose(emission_probability[:,obs_seq[0]])
15     for t in range(1,Col):
16         list_max=[]
17         for n in range(Row):
18             list_x=list(np.array(F[:,t-1])*np.transpose(trainsition_probability[:,n]))
19             #获取最大概率
20             list_p=[]
21             for i in list_x:
22                 list_p.append(i*10000)
23             list_max.append(max(list_p)/10000)
24         F[:,t]=np.array(list_max)*np.transpose(emission_probability[:,obs_seq[t]])
25     return F
26 
27 if __name__=='__main__':
28     #隐藏状态
29     invisible=['Sunny','Cloud','Rainy']
30     #初始状态
31     pi=[0.63,0.17,0.20]
32     #转移矩阵
33     trainsion_probility=[[0.5,0.375,0.125],[0.25,0.125,0.625],[0.25,0.375,0.375]]
34     #发射矩阵
35     emission_probility=[[0.6,0.2,0.15,0.05],[0.25,0.25,0.25,0.25],[0.05,0.10,0.35,0.5]]
36     #最后显示状态
37     obs_seq=[0,2,3]
38     #最后返回一个Row*Col的矩阵结果
39     F=viterbi(trainsion_probility,emission_probility,pi,obs_seq)
40     print(F)

结果：

[[ 0.378　　   0.02835　　      0.00070875]
[ 0.0425 　　 0.0354375 　　 0.00265781]
[ 0.01 　　     0.0165375 　　 0.01107422]]

每列代表Dry,Damp,Soggy的概率，每行代表Sunny,Cloud,Rainy，所以可以看出最大概率的天气为｛Sunny，Cloud，Rainy｝