蓝桥杯算法竞赛系列第三章——细谈递归的bro分治

欢迎回到：遇见蓝桥遇见你，不负代码不负卿！

目录

一、什么是分治

二、面试、竞赛中分治经典题剖析

1、归并排序

2、面试题：计算pow(x, n)

3、竞赛题：多数元素

三、思考题：最大子序和

四、蓝桥结语：遇见蓝桥遇见你，不负代码不负卿！

---

【声明】：这篇博文可能有点拔高，所以铁汁们如果一开始看的有点小艰难的话是很正常的，因为笔者在整理博文的时候也是怪痛苦的，但是没关系哦，一遍没看懂就看上两遍三遍，最好用代码实现出来，图画出来，一步一步来，这样就行啦。

【前言】：因为距离蓝桥杯省赛还有不少时间，接下来笔者更新基础算法模块可能会稍微慢一点，打算一周更新一篇基础算法，肯定会保证质量，不能辜负铁汁们的信任，也不能浪费铁汁们的时间，这样安排的话，大概到十二月初就能把蓝桥杯主要考的算法讲的差不多了，然后接下来呢笔者主要是每天更新一篇LeetCode刷题，进行针对性练习，我会在每天刷的题目中筛选一道最有意义的发出来，和大家一起把基础打牢，记住哦，千万不能一味的图快，还是走的踏实一点比较好。等到十二月，基础算法模块结束，笔者还会开蓝桥杯冲刺辅导专栏，重新将历年来的常考算法再过一遍，不过就不会像现在这样的简单了，而且还会穿插着历年的真题以及大量的针对性练习，所以大家现在就要把基础算法掌握个百分之八十以上哦，千万别像笔者之前一样，看到好文收藏了之后就放在收藏夹里吃灰了。

加油加油

嘿嘿，俺要开始表演了，请看下文哟。

一、什么是分治

分治的定义：将一个大问题分解成若干个子问题，依次解决

注意：分治的中心思想是将大问题切割成一个个小问题

为什么说分治是递归的bro呢？因为求解分治的问题，运用到了递归的算法思想：自己调用自己，所以分治是递归的bro,也是特殊的递归。后面讲到的回溯算法也是特殊的递归哦，笔者在后面会详细介绍的。

分治的解题步骤：（中心思想解题）

1.分解：
将原问题分解为若干个规模较小，相互独立，与原问题相同的子问题。

2.解决：
若干个子问题较小而容易被解决则直接解决，否则再继续分解为更小的子问题，直到容易解决为止。

3.合并：
将已求解的各个子问题的解，逐步合并为原问题的解。

二、面试、竞赛中分治经典题剖析

1、归并排序

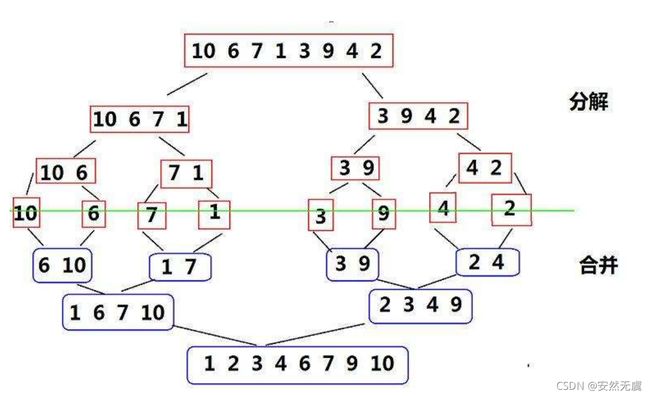
比如一个非常常见的排序，也就是归并排序，它用到的一个算法思想就是分治法。

归并排序，分治法的典型：

• 分解成子问题
• 递归处理子问题
• 合并子问题

#define N 100

void sortArray(int* nums, int left, int right) 
{
    int tmp[N] = { 0 };//tmp作为辅助数组

    //子问题不能接着分解了
    if (left >= right)
        return;
    //分解子问题,并且递归处理
    int mid = (left + right) >> 1;
    sortArray(nums, left, mid);
    sortArray(nums, mid + 1, right);

    //合并子问题
    int k = 0;
    int i = left;
    int j = mid + 1;
    while (i <= mid && j <= right)
    {
        if (nums[i] <= nums[j])
        {
            tmp[k++] = nums[i++];
        }
        else
        {
            tmp[k++] = nums[j++];
        }
    }
    //左半部分有剩余
    while (i <= mid)
    {
        tmp[k++] = nums[i++];
    }
    //右半部分有剩余
    while (j <= right)
    {
        tmp[k++] = nums[j++];
    }
}

 归并排序只简单介绍到这里，铁汁们先了解一下，后面会有专门的排序的模块。

可能讲到这里，咱们还是不太理解什么是分治，没关系，下面的例题会详细讲解的。

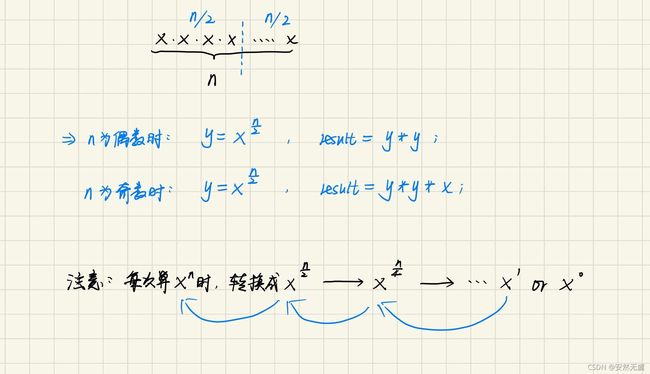
2、面试题：计算pow(x, n)

已知：n >= 0，让我们用分治法解题：

int pow(int x, int n)
{
	int sum = 0;
	//找边界
	if (n == 0)
	{
		return 1;
	}
	if (n == 1)
	{
		return x;
	}
	//n为奇数
	if (n & 1)
	{
		sum = pow(x, n / 2) * pow(x, n / 2) * x;
	}
	//n为偶数
	else
	{
		sum = pow(x, n / 2) * pow(x, n / 2);
	}
	return sum;
}

 但是，面试的时候，当面试官问你还有没有更优解，咋办？

此时确实有一个更为高效的写法，这是在网上看到的一个大佬写的，原理是一样的，只不过没用到递归，节省了很多开销，大家简单了解一下，等到后面笔者能力够的时候，再开设一个专门针对于面试算法的专题。不过在蓝桥杯这里，大家只要理解上面的分治解法就行了。

int pow(int x, int n)
{
	if (n == 0)
	{
		return 1;
	}
	int p = 1;
	while (n > 0)
	{
        //n为奇数时进来
		if (n & 1)
		{
			p = p * x;
		}
		x = x * x;
		n = n / 2;
	}
	return p;
}

3、竞赛题：多数元素

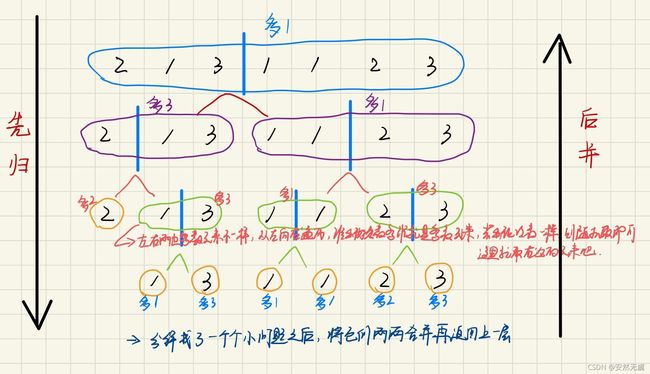
题目描述：给定一个数组，让你找出这个数组中的多数元素，并且数组总是非空的，而且总是存在多数元素的。那什么是多数元素呢？多数元素指的是数组中出现次数大于 n / 2的元素。 

其实用分治法解决本题，多数元素就是数组一分为二...分完之后，每次分完都至少有一半的小数组的多数元素和原数组的多数元素是一样的。如下：

 

 

int majorityElement(int* nums, int numsSize){

    return getMajority(nums, 0, numsSize - 1);
}

int getMajority(int* nums, int left, int right)
{
    //当left == right时代表同时指向一个数，即小数组里只有一个数 
    if(left == right)
    {
        return nums[left];
    }
    int mid = (left + right) >> 1;
    //左边多数元素
    int leftMajority = getMajority(nums, left, mid);
    //右边多数元素
    int rightMajority = getMajority(nums, mid + 1, right);
    //左右两边多数元素相等时
    if(leftMajority == rightMajority)
    {
        return leftMajority;
    }
    //左右两边多数元素不相等，从头到尾遍历两个小数组，看左右两边多数元素谁出现次数多，多的那个就是
    int leftcount = 0;
    int rightcount = 0;
    for(int i = left; i <= right; i++)
    {
        if(nums[i] == leftMajority)
        {
            leftcount++;
        }
        else if(nums[i] == rightMajority)
        {
            rightcount++;
        }
    }
    if(leftcount > rightcount)
    {
        return leftMajority;
    }
    else
    {
        return rightMajority;
    }
}

三、思考题：最大子序和

由于这题比前面几题要多考虑几点，就有一点绕了，所以在这里暂时留作思考题，等铁汁们把前面的三题理解后，在下一篇博文中笔者再详细讲解这一题。先将大致思路讲解一下：

题目描述：给定一个整数数组，找到一个具有最大和的连续子数组（子数组中至少包含一个数），要求返回其最大和。

注意：本题要求的是连续的子数组，可能有的题目要求可以是断开的，但本题不是。

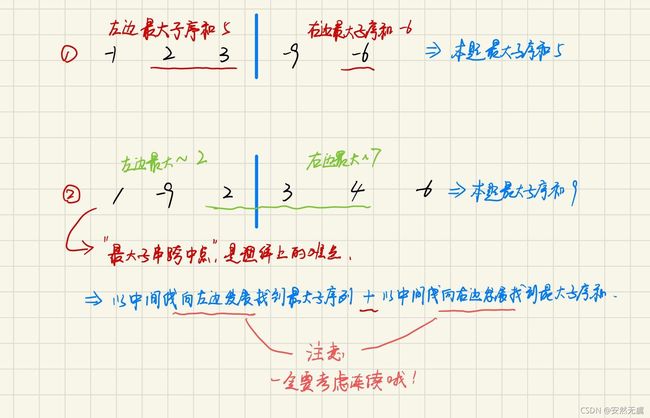
将数组nums由中点mid分为三种情况：

1. 最大子串在左边

2. 最大子串在右边

3. 最大子串跨中点，左右两边元素都有（理解上的难点）

  

本篇思考题就介绍到这里，等到下篇博文中再详细介绍，铁汁们先思考哦。

现在讲解递归（下）里面的思考题，麻烦铁汁们再将上篇博文过一下。

https://blog.csdn.net/weixin_57544072/article/details/120917038?utm_source=app&app_version=4.17.0

递归留下的思考题：放苹果

题目描述：把m个相同的苹果放到n个相同的盘子里，允许有的盘子空着不放，问可以有多少种不同的方法？注意：5 1 1 和 1 5 1是同一种分法

由于这道题目对于没有遇到过的铁汁们可能有点绕，所以我先将大致思路说一下，注意哦，解开本题的话一定要留意今天主要讲的是什么哦。

大致思路：设i个苹果放在k个盘子里的放法总数是：f(i, k), 则：

1、当k > i时，说明盘子比苹果要多，必然有盘子是空的（k - i）个，所以将（k - i）个盘子放在一边不用，剩下的问题就变成了将i个苹果放到i个盘子里，所以当k > i 时，f(i, k) = f(i, i)

2、当k <= i时，将放法分为有盘子为空和无盘子为空两类，所以它的总放法 = 有盘子为空的方法 + 没盘子为空的放法(有盘子为空说明至少有一个盘子为空，所以可以直接将一个空盘子拿到边上去不用，剩下就是将i个苹果放到(k - 1)个盘子里)，所以当k <= i 时，f(i, k) = f(i, k - 1) + f(i - k, k)。为什么说k <= i时，没盘子为空的放法是f(i - k, k)呢，咱们可以这样想：因为苹果比盘子多，我们可以先在每个盘子里放一个苹果，此时剩下（i - k）个苹果，保证没盘子为空是不变的，可变的是什么，可变的是（i - k）个苹果的放法。

 大家将上面理解清楚这题就显得很简单啦，来，代码呈上来...

int f(int m, int n)
{
	//有两个边界
	//不在盘子里放苹果也是一种放法
	if (m == 0)
	{
		return 1;
	}
	//没有盘子就没得放了
	if (n == 0)
	{
		return 0;
	}
	//苹果比盘子少时
	if (m < n)
	{
		return f(m, m);
	}
	//苹果比盘子多时
	return f(m, n - 1) + f(m - n, n);
}
int main()
{
    

四、蓝桥结语：遇见蓝桥遇见你，不负代码不负卿！

OK，分治就介绍到这里咯，本身分治就不比其他算法内容多，而且很多利用到递归的知识，大家可以将递归分治放在一起复习、刷题。好嘞，从明天开始，笔者每一天都会发一篇LeetCode刷题，前期主要是针对于蓝桥杯算法，题目比较简单，笔者和大家一起努力哦，嘿嘿，期待铁汁们留言点评，如果能够再动动小手，给博主来个三连那就更好啦，您的认可就是我最大的动力！