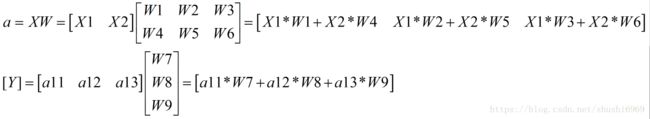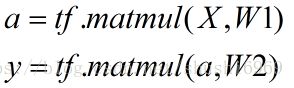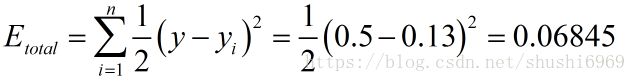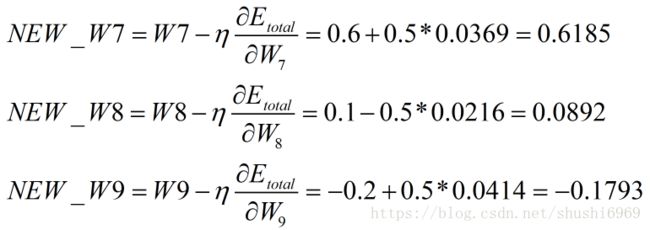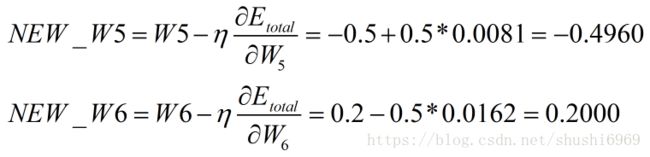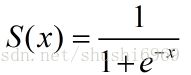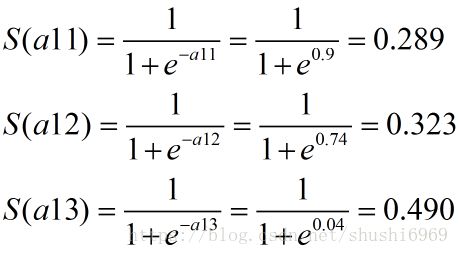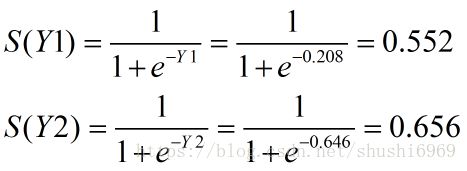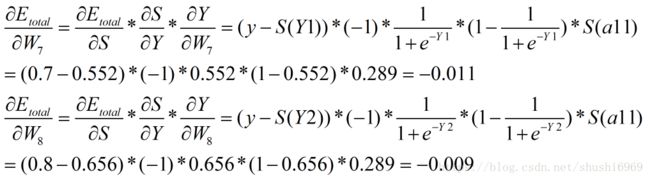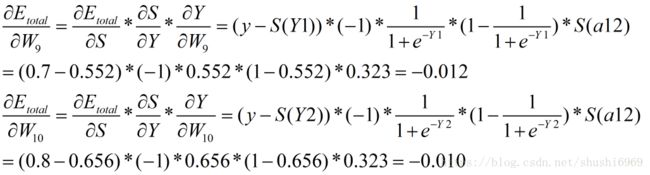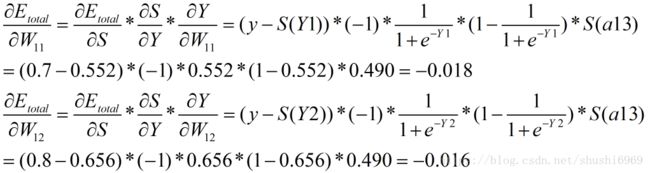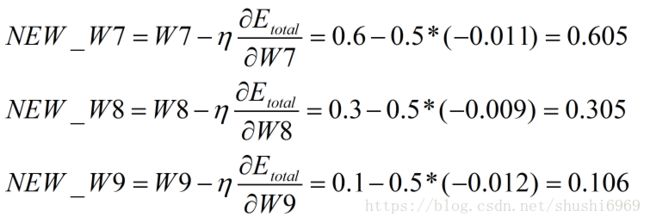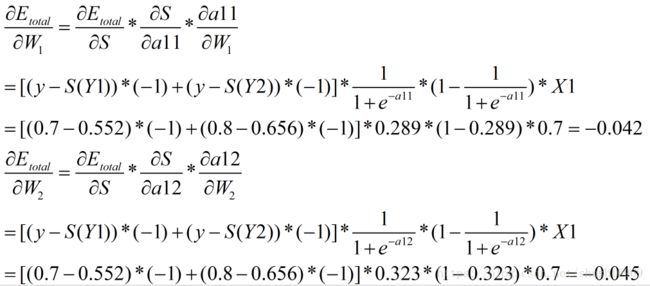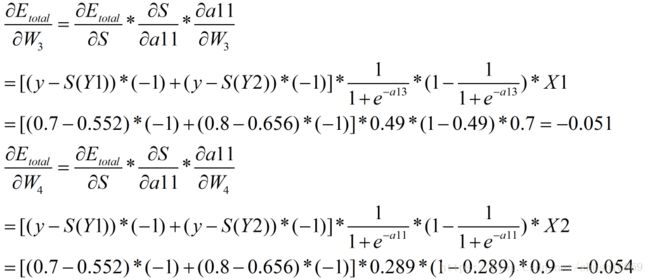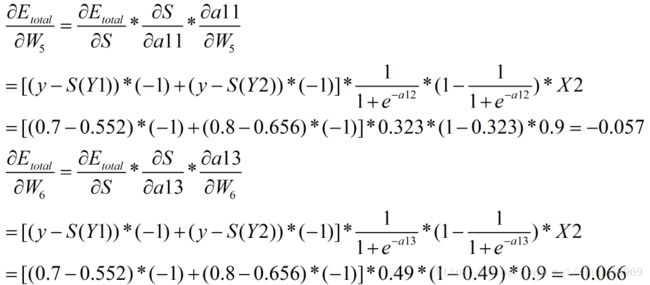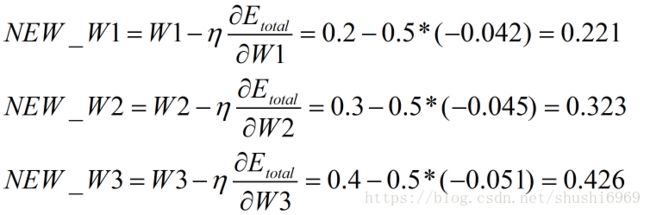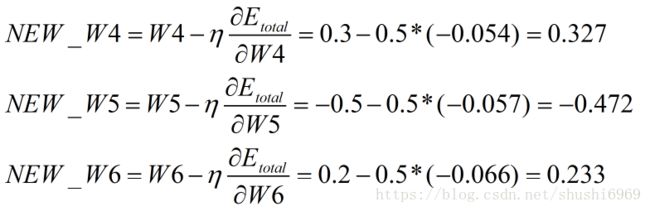前馈神经网络权值更新案例
本章的主要目的是在于用tensorflow实现一个简单的神经网络算法。
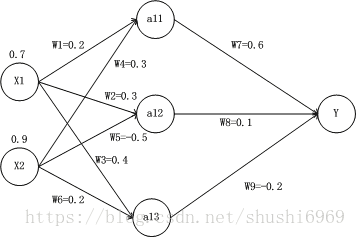
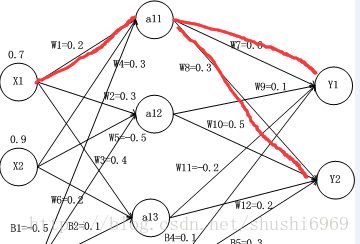
下图是一个简单的前馈神经网络图,改图中有3层结构,第一层为输入层,第二层为隐藏层,第三层则为输出层,图中的W1,……,W9为连接边的权值。下图展示如何进行神经网络的前向传播计算。
1.前向传播计算的手动计算及矩阵表示以及Tensorflow计算代码
(1)计算输入层-->隐藏层的权重
a11 = W1 * X1 + W4 * X2 = 0.2*0.7 + 0.3*0.9 = 0.14 + 0.27 = 0.41
a12 = W2 * X1 + W5 * X2 = 0.3*0.7 + (-0.5)*0.9 = 0.21 - 0.45 = -0.24
a13 = W3 * X1 + W6 * X2 = 0.4*0.7 + 0.2*0.9 = 0.28 + 0.18 = 0.46
(2)计算隐藏层-->输出层的权值
Y = W7 * a11 + W8 * a12 + W9 * a13 = 0.6*0.41 + 0.1*(-0.24) - 0.2*0.46 = 0.13
由于最终Y的值大于0,故Y的结果为正类。
观察上图,输入为X1和X2,将输入转化为矩阵表示X=[x1,x2],权值W为如下所示,隐藏层的a表示如下所示。
将计算输入层-->隐藏层的权重、计算隐藏层-->输出层的权值转化为矩阵表示为
上述是实现一个前馈神经网络计算的一个矩阵表示形式,Y的矩阵取决于样本类别的个数,在Tensorflow中计算如下公式所示:
上述的前馈神经网络只是简单的实现了神经网络的计算过程。神经网络的优化过程就是优化神经元中参数取值的过程。网络中的权值都是预先设置好的,下面我们将使用Tensorflow工具进行权值的训练,即训练模型,下面介绍一下有监督学习的方式来更合理地设置参数取值。
2.不包含激活函数以及池化函数的模型训练
(1)通过上述1节得到了前向传播的值,这里就不再重复。注:把上述的权重都看作为初值
(2)利用反向传播来更新所有的权重
为了方便计算,则将y的实际值设置为0.5。
a.计算总误差(梯度下降方法中有3个方法,本文采用全批量梯度下降方法)
b.隐藏层-->输出层的权值更新
以权重W7为例,我们想知道W7对整体误差产生了多少的影响:
用上述的值来更新W7、W8以及W9的权值。其中,ŋ为学习率,取值为0.5。
c.隐藏层-->输入层的权值更新
该层的计算方法和上述方法基本一致,本文中Y只有一个节点,故上层的影响只有Y没有其他节点。当改层中存在很多个节点时,就需要计算所有节点给W1带来的影响了。为了方便说明这个问题,故引用了其他论文中的图片,该图如下所示,y_k节点受上层的影响。
更新误差一次完成,得到了a11=0.4451,a12=-0.2342,a13=0.04556,Y=0.1727,E_total=0.0536相对于0.0685提高了0.0149。继续更新将完成神经网络的权值更新。
2.使用激活函数以及池化函数的模型训练
该图是上个图的改进版,在图中加入了偏移项,输出节点Y2,激活函数是sigmoid函数,函数如下所示。
(1)计算输入层-->隐藏层的权重
a11 = W1 * X1 + W4 * X2 + b1 * B1 = 0.2*0.7 + 0.3*0.9 - 0.5 = - 0.900
a12 = W2 * X1 + W5 * X2 + b1 * B1 = 0.3*0.7 - 0.5*0.9 - 0.5 = - 0.740
a13 = W3 * X1 + W6 * X2 + b1 * B1 = 0.4*0.7 + 0.2*0.9 - 0.5 = - 0.040
(2)计算隐藏层-->输出层的权值更新
Y1 = S(a11) * W7 + S(a12) * W9 + S(a13) * W11 + b2 * B4 = 0.289*0.6 + 0.323*0.1 + 0.490*(-0.2) + 0.1*1 = 0.208
Y2 = S(a11) * W8 + S(a12) * W10 + S(a13) * W12 + b2 * B5 = 0.289*0.3 + 0.323*0.5 + 0.490*0.2 + 0.3*1 = 0.646
(3)计算总误差
该层的计算方法和上述方法基本一致,本文中Y有二个节点,故上层的影响有Y1和Y2节点。则在计算隐藏层的时候还需要把下一层的节点考虑进来。
为了方便计算,则将Y1的实际值设置为0.7,Y2的实际值设置为0.8。
(4)隐藏层-->输出层的权值更新
(5)计算隐藏层-->输入层的权值
针对该层的权值同时收到Y1和Y2的影响,故和有一个输出节点的计算方法不一样。在计算的时候需要考虑多个输出点。如下图所示。
上述方法即更新完参数。
参考文献:
https://www.cnblogs.com/charlotte77/p/5629865.html
实战Google深度学习框架
http://www.cnblogs.com/charlotte77/p/7783261.html