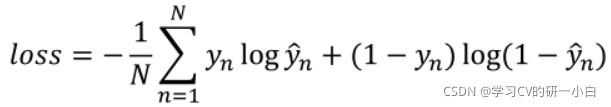PyTorch深度学习——逻辑斯蒂回归(分类问题)(B站刘二大人P6学习笔记)
目录
1 什么是分类问题?
2 为什么要使用逻辑斯蒂回归?
3 Sigmid Founction(逻辑斯蒂回归函数)
3.1 模型的改变
3.2 损失函数的改变(BCE Loss)
3.3 代码的改变
1 什么是分类问题?
分类问题,与之前学习的线性回归问题不同,输出的是分类的概率值,在训练过程中,计算它属于每一个分类的所有概率,其中概率最大的那一种分类,就是我们要的输出结果。
(在PyTorch中 torchvison包 提供一些主流的数据集,root:下载路径。train:是选择训练集还是测试集。download:是否需要下载,第一次使用需要下载)。
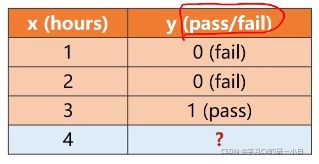
现在我们将之前的学习问题,修改成分类问题,x表示学习时间,y表示通过率,0表示不通过,1表示通过,这也叫做”二分类问题“
2 为什么要使用逻辑斯蒂回归?
在之前我们的学习中,![]() 最终预测的是一个实数,而针对分类问题,我们要把
最终预测的是一个实数,而针对分类问题,我们要把![]() 输出的实数映射成一个0到1的概率(
输出的实数映射成一个0到1的概率( ![]() [0,1] ),这个映射的过程就是本节课所学的逻辑斯蒂回归,逻辑斯蒂回归利用公式
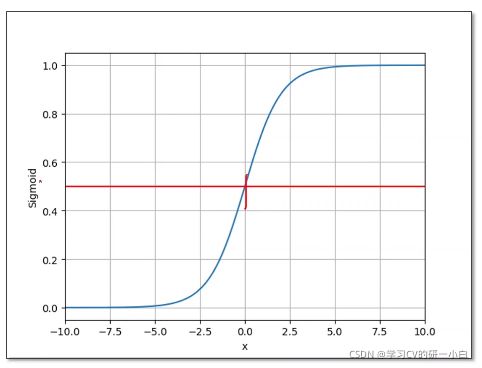
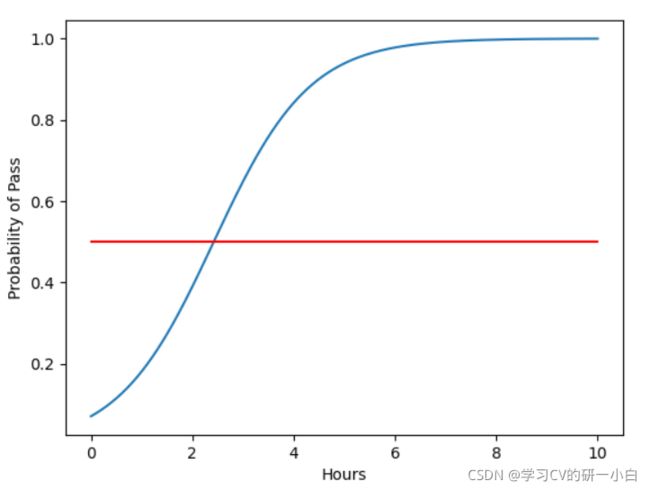
[0,1] ),这个映射的过程就是本节课所学的逻辑斯蒂回归,逻辑斯蒂回归利用公式![]() ,将实数域的数值映射到 [0.1]范围内的概率。逻辑斯蒂函数的图像如下所示:
,将实数域的数值映射到 [0.1]范围内的概率。逻辑斯蒂函数的图像如下所示:
逻辑斯蒂函数在数学界被分为——饱和函数。
计算概率的方式:将原本计算的实数![]() 作为变量输入到逻辑斯蒂函数中,输出的就是映射之后的概率值。
作为变量输入到逻辑斯蒂函数中,输出的就是映射之后的概率值。
3 Sigmid Founction(逻辑斯蒂回归函数)
Sigmid Founction需要满一下三个条件:
- 函数值有极限
- 是单调增函数
- 是饱和函数
Sigmid Founction中最具有典型性的函数就是逻辑斯蒂函数。其他的一些Sigmid Founction如下图所示:
3.1 模型的改变
之前学习的函数与逻辑斯蒂回归函数的计算图的区别:可以看出逻辑斯蒂回归函数在计算出![]() 之后,还多了一步——通过使用逻辑斯蒂回归函数,把实数值映射到【0,1】的区间中,再输出
之后,还多了一步——通过使用逻辑斯蒂回归函数,把实数值映射到【0,1】的区间中,再输出![]() 。
。
注:( ![]() 一般就代表逻辑斯蒂回归)
一般就代表逻辑斯蒂回归)
3.2 损失函数的改变(BCE Loss)
之前学习的函数的损失:计算两个实数值的差值,数轴上的距离
逻辑斯蒂回归函数的损失:输出的是一个分布,需要计算的是两类分布之间的差异,在统计学中的计算方法有——KL散度,cross-entropy(交叉熵)等,这里我们使用的是cross-entropy(交叉熵)方法。
交叉熵:例如:现有两个分布 ![]() 和
和 ![]() ,此时交叉熵公式为:
,此时交叉熵公式为:
这个公式的值表示两个分布之间的差异的大小,值越大,差异越小。在本例中,在公式前加了负号,目的是为了符合我们的平时思维,使Loss越小,差异越小。
具体解释:在本例中,是二分类问题,![]() 的取值只能是0或1,
的取值只能是0或1,![]() 的取值只能
的取值只能 ![]() ,Loss函数如下:
,Loss函数如下:
- 当
 时,
时,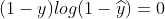 ,此时
,此时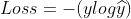 ,因为
,因为 ,
,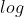 函数是单调递增函数,此时
函数是单调递增函数,此时  越大,也就是越接近1,
越大,也就是越接近1,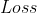 的值越小,差异越小;
的值越小,差异越小; - 当
 时,
时,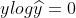 ,此时
,此时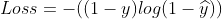 ,因为
,因为 ,
,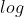 函数是单调递增函数,此时
函数是单调递增函数,此时  越小,也就是越接近0,
越小,也就是越接近0,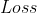 的值越小,差异越小;
的值越小,差异越小;
(有点绕,可以自己多推几次)
最终我们计算的![]() 总和公式如下:
总和公式如下:
补充: 关于交叉熵的详细解释见链接:
一文搞懂交叉熵在机器学习中的使用,透彻理解交叉熵背后的直觉_史丹利复合田的博客-CSDN博客
3.3 代码的改变
- def __init__没有改变:原因是,
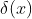 (逻辑斯蒂回归函数)是一个没有参数的函数,不需要在构造函数中进行初始化,直接调用就可以;
(逻辑斯蒂回归函数)是一个没有参数的函数,不需要在构造函数中进行初始化,直接调用就可以;
- 数据集的改变:因为是二分类问题,
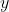 的取值只能是0或1;
的取值只能是0或1;
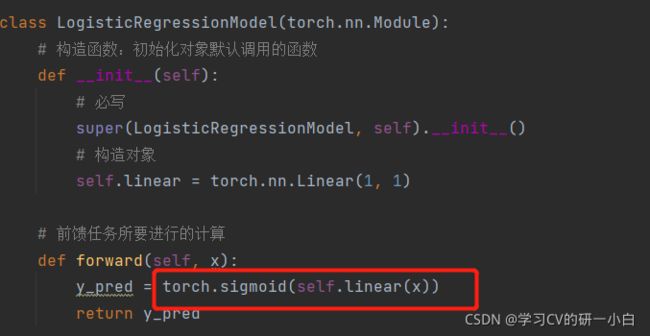
- 模型的改变:由于PyTorch版本更新,不用再导入torch.nn.functional包,可以直接使用包中的Sigmoid函数进行训练,如下图;
- 损失函数的改变:不再使用MSE损失函数,改为使用BCE损失函数,由于PyTorch版本更新,将 size_average=False 更改为 reduction='sum'
完整代码如下:
import matplotlib.pyplot as plt
import torch
import matplotlib.pyplot as pl
import numpy as np
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])
class LogisticRegressionModel(torch.nn.Module):
# 构造函数:初始化对象默认调用的函数
def __init__(self):
# 必写
super(LogisticRegressionModel, self).__init__()
# 构造对象
self.linear = torch.nn.Linear(1, 1)
# 前馈任务所要进行的计算
def forward(self, x):
y_pred = torch.sigmoid(self.linear(x))
return y_pred
# 实例化
model = LogisticRegressionModel()
# 损失函数对象
criterion = torch.nn.BCELoss(reduction='sum')
# 优化器对象
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# 进行训练
for epoch in range(1000):
# 计算y hat
y_pred = model(x_data)
# 计算损失
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
# 所有权重每次都梯度清零
optimizer.zero_grad()
# 反向传播求梯度
loss.backward()
# 更新,step()更新函数
optimizer.step()
# 画图
x = np.linspace(0, 10, 200)
x_t = torch.Tensor(x).view((200, 1))
y_t = model(x_t)
y = y_t.data.numpy()
plt.plot(x, y)
plt.plot([0, 10], [0.5, 0.5], c='r')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid
plt.show()
运行截图如下: