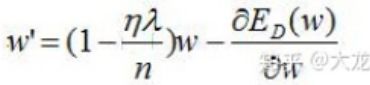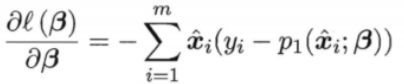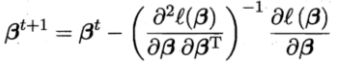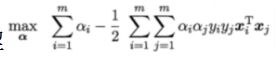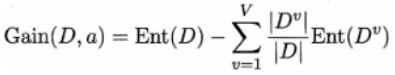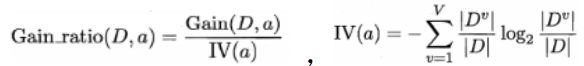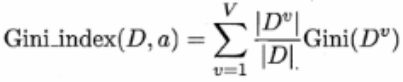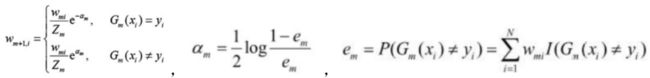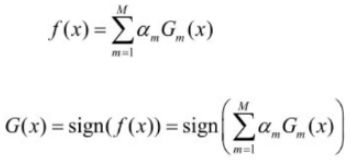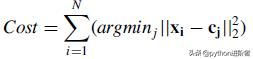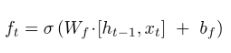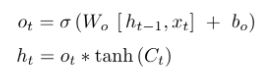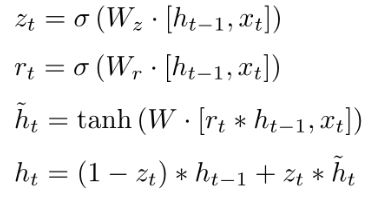机器学习主要知识点整理
目录
- 概率问题
- 各种对比
-
- LR vs SVM
-
- LR 对比 SVM
- 如何选择LR和SVM
- 决策树 vs LR
- GBDT vs LR
- AdaBoost vs GBDT
- GBDT vs XGBoost
- CART vs ID3 vs C4.5
- Boosting vs Bagging
- 第一章 绪论
- 第二章 模型评估与选择
-
- 1.评估方法
- 2.评估指标
- 3.泛化误差期望 = 偏差+方差+噪声
- 4.归一化
- 5.正则化
-
- Q:L1比L2更稀疏
-
- (1)梯度值
- (2)先验概率
- (3)等高线图形方法
- (4)函数叠加方法
- Q:为什么权重变小可以缓解过拟合
- 6.过拟合与欠拟合
-
- (1)降低过拟合:
- (2)降低欠拟合:
- 第三章 线性模型
-
- 1.线性模型的优点
- 2.一元线性回归
- 3.多元线性回归
- 4.对数几率回归(LR)
-
- (1) 二分类,广义线性模型,用Sigmoid
- (2)优点
- (3)缺点
- (4)对数损失函数==极大似然函数取对数
- (5)极大似然法求解w和b
- (6)推导
- (7)为什么用极大似然而不用例如平方损失做优化
- (8)重复特征对结果没啥影响,就是慢,相当于每个特征作用变为原来1/n
- (9)用Sigmoid的理由
- (10)LR和SVM的相同
- (11)LR vs SVM
- (12)如何选择LR和SVM
- (13)LR如何解决线性不可分问题
- (14)LR离散化连续数值
- 5.最大熵模型:学习概率模型时,在所有可能的概率模型中,熵最大的模型是最好的模型。
- 6.线性判别分析LDA
-
- (1)优点:计算速度快、充分利用先验知识
- (2)缺点:非高斯分布时不好(PCA同)、降维后维数最多为n-1,维度高类别少时不好使。
- (3)投影到一条直线上,使同类样例的投影点尽可能接近、异类样例的投影点尽可能远离
- (4)广义瑞利商:类内散度除以类间散度
- 7.多分类 OvO、OvR、MvM
- 8.数据类别不平衡:调整分类阈值、欠采样、过采样
- 9.交叉熵、相对熵(KL散度)、互信息
- 第六章 支持向量机SVM
-
- 1. SVM优点
- 2. SVM缺点
- 3. 为什么SVM转换到对偶问题:对偶问题好求解;可以引入核函数
- 4. SMO算法:每次固定两个α以外的参数,然后更新这俩
- 5. 为什么映射到高维:如果原始空间是有限维,即属性数有限,那么一定存在一个高维特征空间使样本可分
- 6. 常用核函数
- 7.拉格朗日乘子法的条件:目标函数和约束条件都连续可微(目标函数为凸优化)
- 8.LR和SVM的相同
- 9.LR vs SVM
- 10.SVR是一个回归模型,允许f(x)与y有至多epsilon的误差
- 11. 缺失值情况下模型选择
- 第四章决策树DT
-
- 1.CART vs ID3 vs C4.5
- 2.信息熵 & 信息增益
- 3.信息增益率
- 4.基尼指数 & 基尼值
- 5.预剪枝和后剪枝
- 6.连续值处理:二分法进行离散化,得到众多属性,找到信息增益最大的那个作为划分点
- 7.缺失值处理(C4.5):
- 8.CART剪枝:在训练集找到剪枝后和剪枝前损失相同时候对应的α和此时的子树,不断剪枝直到根节点,形成子树序列,根据验证集选择最优子树
- 9.决策树vs LR
- 10.预剪枝停止条件
- 11.树模型不能太稀疏
- 第八章集成学习
-
- 1.根据霍夫丁不等式,多个弱学习器集成的错误率指数下降
- 2.AdaBoost每轮调整样本权重,更关注上一次没学好的样本
- 3.分类器组合(相当于加权投票)
- 4.AdaBoost:加性模型,损失是指数函数,学习算法为前向分步算法时的二分类学习方法
- 5.GBDT:二叉cart树,分类、回归,树的累加没有α系数,先计算已有t-1树的负梯度,在平方损失下就是残差,让待学习的树去拟合负梯度(残差)
- 6.XGBoost
-
- (1)目标函数在t-1那棵树上进行了二阶泰勒展开,且自带了正则化(限制树的数量和w参数二范式)
- (2)寻找划分点
- (3)近似算法优点:减少划分点数目,提高速度;一定程度防止过拟合;存int,开销小
- (4)并行特征选择:XGB的并行主要是在特征选择的时候将数据放到多个block上,然后使用多线程并行得到各个特征的最佳划分点,各个基学习器还是串行训练的
- (5)缺失值处理
- (6)参数
- (7)特征重要性
- 7.AdaBoost vs GBDT
- 8.GBDT vs XGBoost
- 9.GBDT vs LR
- 10.Bagging:基于自助采样,造好多树,因为采样所以树都不一样;分类投票,回归平均
- 11.RF随机森林:在Bagging基础上,引入随机属性选择,随机选k个(推荐k=log2 d)
- 12.随机森林简单易实现、计算开销小,性能不错
- 13.Boosting vs Bagging
- 14.为什么决策树当基分类器:
- 15.Bagging注重方差,Boosting注重偏差
- 第九章 聚类
-
- Kmeans
- 密度聚类 DBSCAN
- 层次聚类 AGNES
- 深度学习
-
- 1.优化算法:SGD、Adam、牛顿法
- 2. 激活函数
-
- sigmoid
- Tanh(输出0均值)
- ReLU
- Softmax、交叉熵
- 3. 平方损失 & 交叉熵损失
-
- 适合场景
- 为什么平方损失不适合Sigmoid或Softmax
- 4. BN、LN等
-
- 为什么要归一化
- 公式
- 5.dropout
-
- 以一定概率p让神经元输出,有可能就不输出
- 但是要保证数据分布相同,训练的时候除以p,或者测试的时候乘p
- 解决过拟合
- 使用位置(rnn和cnn不用)
- 6.过拟合与欠拟合
-
- (1)降低过拟合:
- (2)降低欠拟合:
- 7. 参数初始化方法
- 8. RNN & LSTM & GRU
-
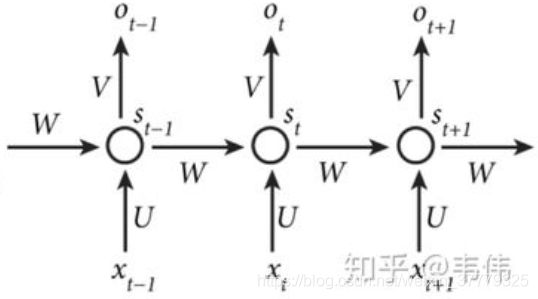
- RNN
- LSTM(用了三个门来控制信息传递的程度)
- GRU(整合了一下LSTM的遗忘门和输入门,还有cell跟hidden)
- 9. 梯度消失和爆炸怎么解决
- 10.交叉熵、相对熵(KL散度)、互信息
- 11. LSTM为什么用sigmoid和tanh
- 12. LSTM的tanh能不能换ReLU
- 13. pytorch实现一个attention
- 14. [1574.删除最短的子数组使剩余数组有序](https://leetcode-cn.com/problems/shortest-subarray-to-be-removed-to-make-array-sorted/)
概率问题
贝叶斯估计推理
各种对比
LR vs SVM
LR 对比 SVM
- LR是参数模型,SVM是非参数模型
- LR用对数似然函数,SVM用hinge loss
- SVM只考虑支持向量,LR全局
- LR给概率,SVM只能分类
如何选择LR和SVM
- 如果Feature的数量很大,跟样本数量差不多,这时候选用LR或者是Linear Kernel的SVM
- 如果Feature的数量比较小,样本数量一般,不算大也不算小,选用SVM+Gaussian Kernel
- 如果Feature的数量比较小,而样本数量很多,需要手工添加一些feature变成第一种情况。或者上深度学习
决策树 vs LR
GBDT vs LR
- 决策边界:线性回归是一条直线;LR是曲线;GBDT可能是多条线
- GBDT并不一定总好于其他(没有免费午餐原则)
AdaBoost vs GBDT
- AdaBoost:调整样本权值;组合方式加权多数表决;一般用来分类
- GBDT:向负梯度方向优化;将弱分类器叠加;用cart树;目标函数可选多;一般用来回归
GBDT vs XGBoost
- Xgb是GBDT的工程实现
- XGBoost显示加入了正则项,GBDT在构建完树之后才剪枝
- GBDT使用一阶导,XGB用了二阶泰勒展开
- GBDT用cart树,XGB支持多种,包括线性分类器
- GBDT每轮用全部数据,XGBoost类似随机森林,支持采样(列抽样)
- GBDT没有缺失值处理,XGBoost能处理
- XGBoost并行计算
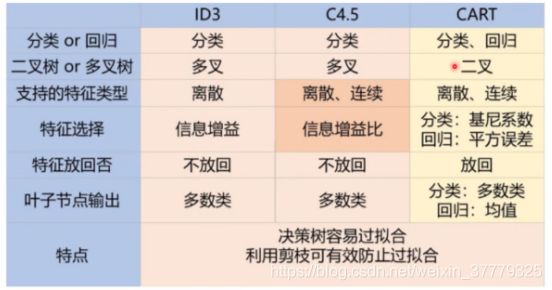
CART vs ID3 vs C4.5
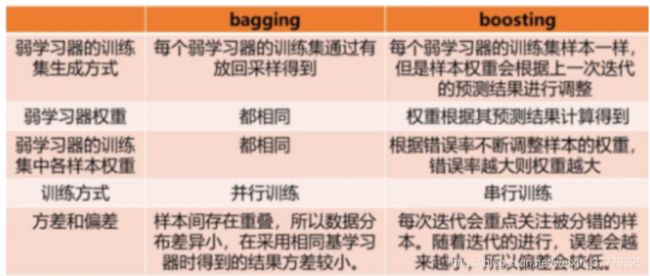
Boosting vs Bagging
第一章 绪论
第二章 模型评估与选择
1.评估方法
留出法、交叉验证、自助法(有放回采样,bagging,没选中的概率1/e=0.368)
2.评估指标
(1)查准率Precision P = TP/(TP + FP), 查全率Recall R = TP/(TP+FN)
p-r曲线比面积,F1是调和平均,或者Fβ是加权调和平均
(2)ROC与AUC
TPR = TP/TP+FN 敏感性 所有正样本中有多少被预测为正例
FPR = FP/TN+FP 特异性 所有负样本中有多少被预测为正例
当正负样本的分布发生变化时,ROC曲线的形状能够基本保持不变,而P-R曲线的形状一般会发生较剧烈的变化。
(3)AUC计算方法
AUC是衡量二分类模型优劣的一种评价指标,表示预测的正例排在负例前面的概率。
3.泛化误差期望 = 偏差+方差+噪声
4.归一化
Min-Max Scaling、Z-Score Normalization,决策树不需要归一化,其它通过梯度下降的要
5.正则化
Q:L1比L2更稀疏
(1)梯度值
L2和L1在w的系数不同,导致w趋向于0的时候参数减小就很慢,而L1就容易变0。
(2)先验概率
(3)等高线图形方法
(4)函数叠加方法
Q:为什么权重变小可以缓解过拟合
A:在过拟合的时,拟合函数的系数往往非常大。过拟合,就是拟合函数需要顾忌每一个点,最终形成的拟合函数波动很大。在某些很小的区间里,函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值(绝对值)非常大,由于自变量值可大可小,所以只有系数足够大,才能保证导数值很大。
而正则化是通过约束参数的范数使其不要太大,所以可以在一定程度上减少过拟合情况。
6.过拟合与欠拟合
(1)降低过拟合:
- 扩增数据
- 降低模型复杂度(采取合适的模型、降低特征数量、BN、Dropout、EarlyStopping)
- 正则化
- 集成学习
(2)降低欠拟合:
- 添加特征
- 增加模型复杂度
- 减小正则化系数
第三章 线性模型
1.线性模型的优点
形式简单、易于建模、有很好的可解释性
2.一元线性回归
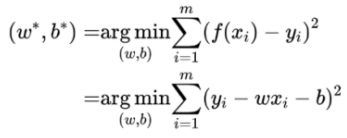
基于均方误差最小化来进行模型求解的方法称为“最小二乘法”
对w和b求偏导得0后解得:

3.多元线性回归

X为满秩矩阵或正定矩阵时
![]()
反之,有多个解,可引入正则化进行约束选择
4.对数几率回归(LR)
(1) 二分类,广义线性模型,用Sigmoid
(2)优点
- 形式简单,模型的可解释性非常好
- 模型效果不错,可并行开发
- 训练速度较快
- 资源占用小
- 方便输出结果调整(输出的是概率,定阈值就行)
(3)缺点
- 准确率不高(模型简单);
- 难处理数据不平衡;
- 无法筛选特征。
(4)对数损失函数==极大似然函数取对数
(5)极大似然法求解w和b

对率回归模型最大化“对数似然”(loglikelihood),即令每个样本属于其真实标记的概率越大越好
(6)推导
(7)为什么用极大似然而不用例如平方损失做优化
用极大似然函数梯度下降和xy相关,与sigmoid无关,比较稳定,如果用平方损失函数更新就与sigmoid的梯度相关,其梯度不大于0.25,训练缓慢。
(8)重复特征对结果没啥影响,就是慢,相当于每个特征作用变为原来1/n
(9)用Sigmoid的理由
- 伯努利分布属于指数族分布,带入后求解得到映射函数为Sigmoid
伯努利分布和指数族分布的概率公式进行对比,可以得到 T ( Y ) = Y T(Y) = Y T(Y)=Y,然后 h ( x ) = E ( T ( Y ) ) = E ( Y ) = θ h(x) = E(T(Y)) = E(Y) = \theta h(x)=E(T(Y))=E(Y)=θ,其中 η = w T x = l n θ 1 − θ \eta = w^Tx = ln \frac{\theta}{1-\theta} η=wTx=ln1−θθ,可以反推出 θ = e η 1 + e η \theta = \frac{e^\eta}{1 + e^\eta} θ=1+eηeη,所以有 h ( x ) = e η 1 + e η = e w T x 1 + e w T x h(x) = \frac{e^\eta}{1 + e^\eta} = \frac{e^{w^Tx}}{1 + e^{w^Tx}} h(x)=1+eηeη=1+ewTxewTx,也就是说连接函数的形式就是sigmoid - 二分类,带入最大熵模型的特征函数求得的概率公式就是使用了Sigmoid。
(10)LR和SVM的相同
- 可以分类,一般二分类
- 可以加正则化(SVM自带)
- 监督学习
- 判别模型
(11)LR vs SVM
- LR是参数模型,SVM是非参数模型
- LR用对数似然函数,SVM用hinge loss
- SVM只考虑支持向量,LR全局
- LR给概率,SVM只能分类
(12)如何选择LR和SVM
- 如果Feature的数量很大,跟样本数量差不多,这时候选用LR或者是Linear Kernel的SVM
- 如果Feature的数量比较小,样本数量一般,不算大也不算小,选用SVM+Gaussian Kernel
- 如果Feature的数量比较小,而样本数量很多,需要手工添加一些feature变成第一种情况。或者上深度学习
(13)LR如何解决线性不可分问题
- 核函数
- 扩展LR算法,提出FM(因子分解)算法;
- 特征组合
(14)LR离散化连续数值
- 离散特征容易增减,易于模型快速迭代;
- 稀疏向量内积乘法计算快,好存储;
- 鲁棒性强(年龄>30,如果有个300的不离散gg);
- 离散化后每个变量具有单独的权重,相当于引入非线性,提升模型表达能力;
- 可以特征交叉;
- 模型更稳定,类似鲁棒性;简化模型,防止过拟合。
5.最大熵模型:学习概率模型时,在所有可能的概率模型中,熵最大的模型是最好的模型。
6.线性判别分析LDA
(1)优点:计算速度快、充分利用先验知识
(2)缺点:非高斯分布时不好(PCA同)、降维后维数最多为n-1,维度高类别少时不好使。
(3)投影到一条直线上,使同类样例的投影点尽可能接近、异类样例的投影点尽可能远离
(4)广义瑞利商:类内散度除以类间散度
7.多分类 OvO、OvR、MvM
8.数据类别不平衡:调整分类阈值、欠采样、过采样
9.交叉熵、相对熵(KL散度)、互信息
相对熵 = 交叉熵 - 熵:

互信息(信息熵):X,Y的联合分布P(X,Y)与乘积分布P(X)P(Y)的相对熵,等于熵-条件熵

第六章 支持向量机SVM
1. SVM优点
- 凸优化问题全局最优
- 线性和非线性(核方法)都能用;
- 只取决于支持向量
2. SVM缺点
- 二次规划问题求解将涉及m阶矩阵的计算(m为样本的个数), 因此SVM不适用于超大数据集。(SMO算法可以缓解这个问题)复杂度 O(km2)
- 对缺失数据敏感,无处理策略
- 模型稳定性低,输入的微小变化会使得模型难以收敛
3. 为什么SVM转换到对偶问题:对偶问题好求解;可以引入核函数
4. SMO算法:每次固定两个α以外的参数,然后更新这俩
5. 为什么映射到高维:如果原始空间是有限维,即属性数有限,那么一定存在一个高维特征空间使样本可分
6. 常用核函数

如果Feature的数量很大,跟样本数量差不多,这时候选用LR或者是Linear Kernel的SVM
如果Feature的数量比较小,样本数量一般,不算大也不算小,选用SVM+Gaussian Kernel
如果Feature的数量比较小,而样本数量很多,需要手工添加一些feature变成第一种情况。或者上深度学习
7.拉格朗日乘子法的条件:目标函数和约束条件都连续可微(目标函数为凸优化)
8.LR和SVM的相同
- 分类,一般二分类
- 可以加正则化(SVM自带)
- 监督学习
- 判别模型
- 缺失值敏感
9.LR vs SVM
- LR是参数模型,SVM是非参数模型
- LR用对数似然函数,SVM用hinge loss
- SVM只考虑支持向量,LR全局
- LR给概率,SVM只能分类
10.SVR是一个回归模型,允许f(x)与y有至多epsilon的误差
11. 缺失值情况下模型选择
- 数据量很小,用朴素贝叶斯
- 数据量适中或者较大,用树模型,优先 xgboost
- 数据量较大,也可以用神经网络
- 避免使用距离度量相关的模型,如KNN和SVM
第四章决策树DT
1.CART vs ID3 vs C4.5
2.信息熵 & 信息增益
3.信息增益率
4.基尼指数 & 基尼值
5.预剪枝和后剪枝
预剪枝:决策树生成过程中停止
后剪枝:生成完整决策树,然后判断能否替换
6.连续值处理:二分法进行离散化,得到众多属性,找到信息增益最大的那个作为划分点
7.缺失值处理(C4.5):
缺失值属性的信息增益:无缺失值样本所占的比例乘以无缺失值样本子集的信息增益。
样本划分:将缺失值样本按不同的概率划分到了所有分支中,而概率则等于无缺失值样本在每个分支中所占的比例。
测试的时候就是得到一堆的概率分布,取概率最大的那个。
8.CART剪枝:在训练集找到剪枝后和剪枝前损失相同时候对应的α和此时的子树,不断剪枝直到根节点,形成子树序列,根据验证集选择最优子树
9.决策树vs LR
10.预剪枝停止条件
- 只剩一类了
- 信息熵不怎么变
- 设置最小叶子节点的样本数
11.树模型不能太稀疏
在模型都普遍带有正则项时,LR是不让权重W过大,而树控制的是深度、叶节点数量,当在高维系数数据中,某类样本刚好在某一维特征上都是1,而因为稀疏性,其他样本都是0,这样就导致树很容易根据这个维度将样本分为两类,导致在测试集上效果变差,即容易过拟合。而对于LR模型,如果针对这个维度的W特别大会被正则修正。
第八章集成学习
1.根据霍夫丁不等式,多个弱学习器集成的错误率指数下降
2.AdaBoost每轮调整样本权重,更关注上一次没学好的样本
3.分类器组合(相当于加权投票)
4.AdaBoost:加性模型,损失是指数函数,学习算法为前向分步算法时的二分类学习方法
5.GBDT:二叉cart树,分类、回归,树的累加没有α系数,先计算已有t-1树的负梯度,在平方损失下就是残差,让待学习的树去拟合负梯度(残差)
6.XGBoost
(1)目标函数在t-1那棵树上进行了二阶泰勒展开,且自带了正则化(限制树的数量和w参数二范式)
(2)寻找划分点
- GBDT:遍历所有特征和所有取值找增益最大的那个分裂
- XGBoost:近似算法,分箱(分位数法、加权分位数法),减少划分点;将特征的值根据候选划分点分到对应的桶中,对桶中所有样本的一阶导数值和二阶导数值进行累加,得到统计值G, H后,计算每个候选划分点的分裂增益,找到最佳划分点
- 加权分位数法:不是简单的均匀划分,而是对二阶导统计量占比均匀划分
(3)近似算法优点:减少划分点数目,提高速度;一定程度防止过拟合;存int,开销小
(4)并行特征选择:XGB的并行主要是在特征选择的时候将数据放到多个block上,然后使用多线程并行得到各个特征的最佳划分点,各个基学习器还是串行训练的
(5)缺失值处理
为稀疏/缺失值选择一个默认方向;将稀疏/缺失值分别放在左分支和右分支,计算各自对
应的增益。比较两者的增益来选择往左还是往右作为默认方向。
预测:如果训练的时候特征出现过缺失值,就按照当时划分的方向走,不然就默认一个
(6)参数
(7)特征重要性
①gain 增益意味着相应的特征对通过对模型中的每个树采取每个特征的贡献而计算出的模型的相对贡献。与其他特征相比,此度量值的较高值意味着它对于生成预测更为重要。
②cover 覆盖度量指的是与此功能相关的观测的相对数量。例如,如果您有100个观察值,4个特征和3棵树,并且假设特征1分别用于决定树1,树2和树3中10个,5个和2个观察值的叶节点;那么该度量将计算此功能的覆盖范围为10 + 5 + 2 = 17个观测值。这将针对所有4项功能进行计算,并将以17个百分比表示所有功能的覆盖指标。
③freq 频率(频率)是表示特定特征在模型树中发生的相对次数的百分比。在上面的例子中,如果feature1发生在2个分裂中,1个分裂和3个分裂在每个树1,树2和树3中;那么特征1的权重将是2 + 1 + 3 = 6。特征1的频率被计算为其在所有特征的权重上的百分比权重。
7.AdaBoost vs GBDT
- AdaBoost:调整样本权值;组合方式加权多数表决;一般用来分类
- GBDT:向负梯度方向优化;将弱分类器叠加;用cart树;目标函数可选多;一般用来回归
8.GBDT vs XGBoost
- Xgb是GBDT的工程实现
- XGBoost显示加入了正则项,GBDT在构建完树之后才剪枝
- GBDT使用一阶导,XGB用了二阶泰勒展开
- GBDT用cart树,XGB支持多种,包括线性分类器
- GBDT每轮用全部数据,XGBoost类似随机森林,支持采样(列抽样)
- GBDT没有缺失值处理,XGBoost能处理
- XGBoost并行计算
9.GBDT vs LR
- 决策边界:线性回归是一条直线;LR是曲线;GBDT可能是多条线
- GBDT并不一定总好于其他(没有免费午餐原则)
10.Bagging:基于自助采样,造好多树,因为采样所以树都不一样;分类投票,回归平均
11.RF随机森林:在Bagging基础上,引入随机属性选择,随机选k个(推荐k=log2 d)
12.随机森林简单易实现、计算开销小,性能不错
13.Boosting vs Bagging
14.为什么决策树当基分类器:
- 方便整合样本权重到训练过程,不需要过采样
- 调节树的层数可以调节表达能力和泛化能力
- 树的稳定性差,多样性好,适合,随机性高
15.Bagging注重方差,Boosting注重偏差
第九章 聚类
Kmeans
-
流程
-
缺点
- 受初值和离群值的影响,每次的结果都不稳定
- 结果通常不是全局最优而是局部最优
- 无法很好的解决数据簇分布差别比较大的情况
- 不太适用于离散分类
- 样本点只能被分到单一的类中
-
优点
- 针对大数据集是可伸缩和高效的
- 时间复杂度低
- 局部最优已经满足基本需求
-
调优
-
改进
- kmeans++
- ISODATA:不用固定k,当某类样本数过少时,删去该类;当某类样本数过多时,分成两类
密度聚类 DBSCAN
- 基于密度的聚类,假设聚类结构能够通过样本分布的紧密程度确定
层次聚类 AGNES
- 树形聚类结构
- 初始将每个样本看作一个簇,距离最近的两个簇合并,该过程不断重复,直至到达预设的聚类簇个数
深度学习
1.优化算法:SGD、Adam、牛顿法
牛顿法:二阶泰勒展开求偏导为0,求解,收敛速度快,计算复杂度大
SGD:朝负梯度方向下降
动量法:当前时刻的更新与上一时刻有关
AdaGrad:更新频率低的参数可以拥有较大的更新步幅,更新频率高的参数步幅可以较小。梯度除以根号下梯度平方的累加

RMSPop:AdaGrad的改进。下面不是 ( 1 + β ) (1+\beta) (1+β)是 ( 1 − β ) (1-\beta) (1−β),作为衰减因子引入的。

Adam:记录梯度的一阶矩和二阶矩,也就是历史与当前的平均和历史与当前的平方的平均

m是一阶矩,v是二阶矩
深度学习 — 优化入门二(SGD、动量(Momentum)、AdaGrad、RMSProp、Adam详解)
2. 激活函数
sigmoid
- 梯度爆炸(不太容易)
- 梯度消失
- 幂运算,耗时
- 不是零均值,会导致样本只往一个方向更新
Tanh(输出0均值)
ReLU
优点:
- 解决梯度消失
- 计算速度快
- 收敛速度快
- 输出一部分0,产生稀疏性,缓解过拟合
缺点: - 不是全区间可导
- 不是0均值
- Dead ReLU Problem (初始化不合适 or 学习率太大,可以改用其他初始化方法、调节lr或者用adagrad等)
Softmax、交叉熵
Softmax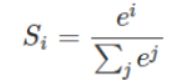
交叉熵
求导简单,对于对的那个参数直接-1,对于错的那个参数不用动
缺点:数值不稳定,可以减去最大值,有个0,分母至少就有个1了
进一步改进,不用全算完分数再求log,可以把分子分母的log变成log分子减去log分母,就不会溢出了
softmax溢出问题

3. 平方损失 & 交叉熵损失
适合场景
- 平方损失适合输出连续,且最后一层不含Sigmoid或Softmax的神经网络
- 交叉熵损失适合二分类或多分类场景
为什么平方损失不适合Sigmoid或Softmax

后一项是激活函数的导数,sigmoid的导数数值太小了,用交叉熵的话,导数是![]() 是线性的,不会出现学习速度过慢的问题
是线性的,不会出现学习速度过慢的问题
4. BN、LN等
- BN是以通道为索引,对NHW(其中N是样本数)进行均值方差计算
- LN是按照CHW,与batch无关
为什么要归一化
为了保证数据在每一层的数据分布都相同,不至于样本一会儿大一会儿小还得找平衡
公式
5.dropout
以一定概率p让神经元输出,有可能就不输出
但是要保证数据分布相同,训练的时候除以p,或者测试的时候乘p
解决过拟合
- 取平均,类似集成学习
- 减少神经元之间复杂的共适应关系
- 类似于性别在生物进化中的角色
使用位置(rnn和cnn不用)
在神经元数量多的全连接层之类的地方前面用,dropout-FC-BN-ReLU
6.过拟合与欠拟合
(1)降低过拟合:
- 扩增数据
- 降低模型复杂度(采取合适的模型、降低特征数量、BN、Dropout、EarlyStopping)
- 正则化
- 集成学习
(2)降低欠拟合:
- 添加特征
- 增加模型复杂度
- 减小正则化系数
7. 参数初始化方法
-
正交初始化(缓解RNN参数连乘的梯度消失、爆炸)
-
随机初始化
8. RNN & LSTM & GRU
RNN
LSTM(用了三个门来控制信息传递的程度)
GRU(整合了一下LSTM的遗忘门和输入门,还有cell跟hidden)
9. 梯度消失和爆炸怎么解决
- 用ReLU、maxout等激活函数
- 用BN
- 梯度裁剪
- 权重正则化
- 残差
10.交叉熵、相对熵(KL散度)、互信息
相对熵 = 交叉熵 - 熵:

互信息(信息增益):X,Y的联合分布P(X,Y)与乘积分布P(X)P(Y)的相对熵,等于熵-条件熵

11. LSTM为什么用sigmoid和tanh
- sigmoid当门控,0-1,用来遗忘和保留
- tanh用来线性变换,-1~1,0中心,在0附近梯度大,收敛快
12. LSTM的tanh能不能换ReLU
ReLU在这里只能缓解梯度爆炸,不能根本上解决,而且会让RNN输出值很大(也有人实验说ReLU效果还行)
13. pytorch实现一个attention
import torch
class self_attention(torch.nn.Module):
def __init__(self):
super(self_attention, self).__init__()
self.query = torch.nn.Linear(128, 128)
self.key = torch.nn.Linear(128, 128)
self.value = torch.nn.Linear(128, 128)
self.softmax = torch.nn.Softmax(-1)
def forward(self, x):
q = self.query(x)
k = self.key(x).permute(0,2,1)
v = self.value(x) # 8 * 64 * 128
attention_map = self.softmax(torch.matmul(q, k)) # 8 * 64 * 64
output = torch.matmul(attention_map, v)
return output
x = torch.randn([8, 64, 128])
m = self_attention()
m(x)
14. 1574.删除最短的子数组使剩余数组有序
class Solution:
def findLengthOfShortestSubarray(self, arr: List[int]) -> int:
n = len(arr)
left = 0
for i in range(1,n):
if arr[i] >= arr[i-1]:
left = i
else:
break
if left == n-1: return 0
right = n-1
for i in range(n-2, -1,-1):
if arr[i] <= arr[i+1]:
right = i
else:
break
ans = min(n+1-left, right)
for i in range(left, -1,-1):
j = right
while j < n and arr[i] > arr[j]:
j += 1
ans = min(ans, j-i-1)
return ans