学习线性判别准则（LDA）和线性分类算法（支持向量机,SVM）。采用Sklearn库

一.编程生成模拟数据集，进行LDA算法练习

1.包引入与生成模拟数据集

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as lda
from sklearn.datasets._samples_generator import make_classification 
import matplotlib.pyplot as plt 
import numpy as np
import pandas as pd
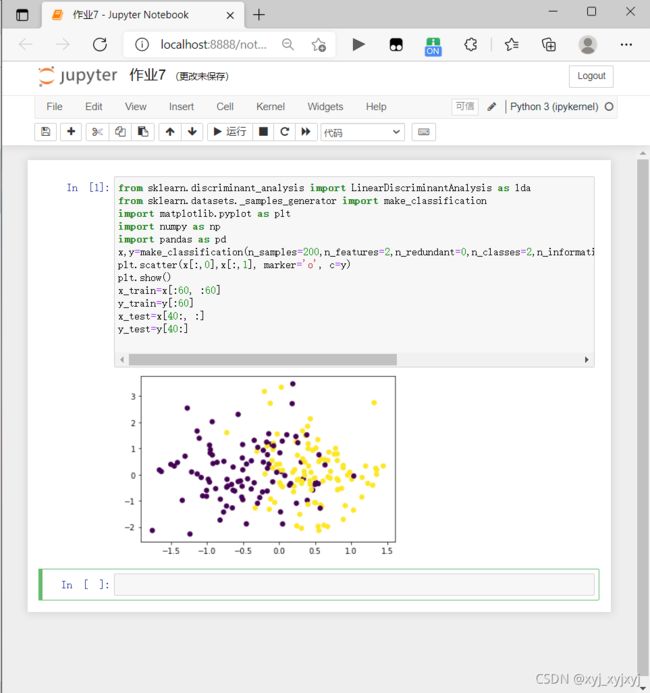
x,y=make_classification(n_samples=200,n_features=2,n_redundant=0,n_classes=2,n_informative=1,n_clusters_per_class=1,class_sep=0.5,random_state=100)
plt.scatter(x[:,0],x[:,1], marker='o', c=y)
plt.show()
x_train=x[:60, :60]
y_train=y[:60]
x_test=x[40:, :]
y_test=y[40:]

2.数据集分组

x_train=x[:150, :150]
y_train=y[:150]
x_test=x[50:, :]
y_test=y[50:]
lda_test=lda()
lda_test.fit(x_train,y_train)
predict_y=lda_test.predict(x_test)
count=0
for i in range(len(predict_y)):
    if predict_y[i]==y_test[i]:
        count+=1
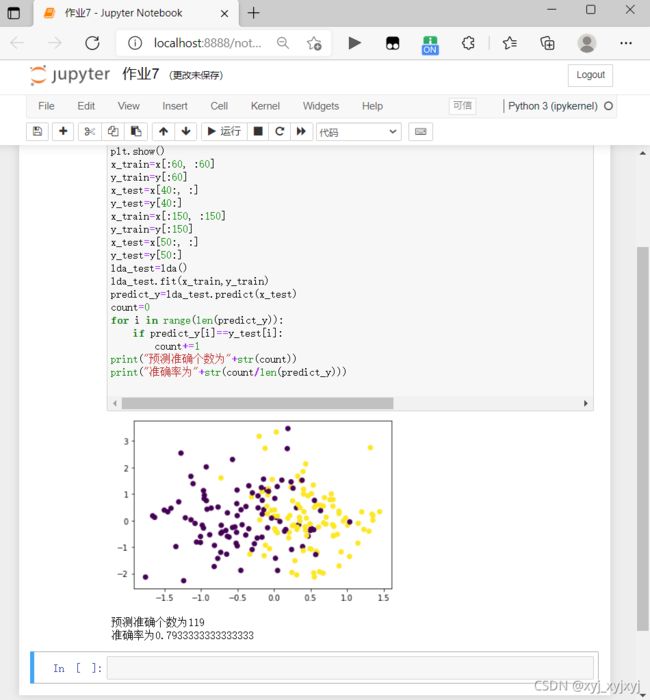
print("预测准确个数为"+str(count))
print("准确率为"+str(count/len(predict_y)))

二.对月亮数据集进行SVM分类，分别采用线性核、多项式核和高斯核以及不同的参数（比如惩罚系数C），对比分析结果

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_moons

X,y = make_moons(n_samples=200,random_state=0,noise=0.05)

h = .02  


C = 1.0 
svc = svm.SVC(kernel='linear', C=C).fit(X, y)
rbf_svc = svm.SVC(kernel='rbf', gamma=0.7, C=C).fit(X, y)
poly_svc = svm.SVC(kernel='poly', degree=3, C=C).fit(X, y)
lin_svc = svm.LinearSVC(C=C).fit(X, y)

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))

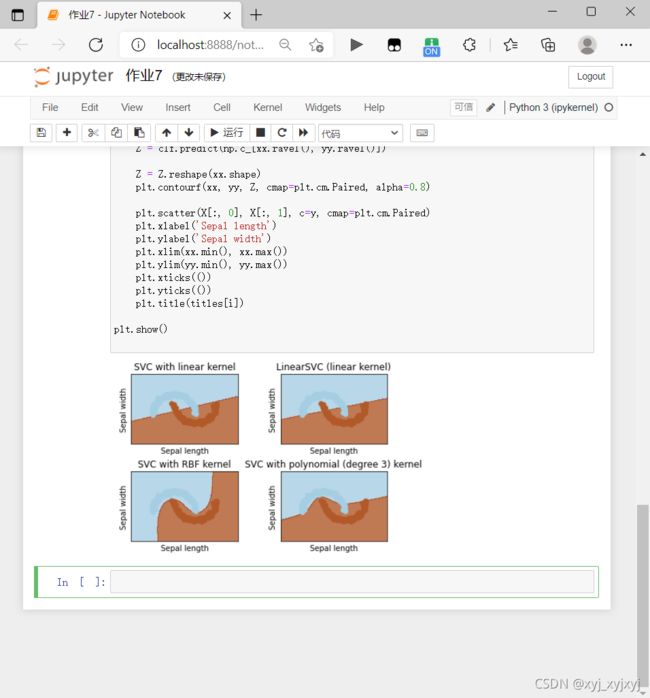
titles = ['SVC with linear kernel',
          'LinearSVC (linear kernel)',
          'SVC with RBF kernel',
          'SVC with polynomial (degree 3) kernel']


for i, clf in enumerate((svc, lin_svc, rbf_svc, poly_svc)):
    plt.subplot(2, 2, i + 1) 
    plt.subplots_adjust(wspace=0.4, hspace=0.4)

    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    
    Z = Z.reshape(xx.shape) 
    plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8) 

    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
    plt.xlabel('Sepal length')
    plt.ylabel('Sepal width')
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.xticks(())
    plt.yticks(())
    plt.title(titles[i])

plt.show()

三.总结

优点

可以解决高维问题，即大型特征空间；
解决小样本下机器学习问题；
能够处理非线性特征的相互作用；
无局部极小值问题；（相对于神经网络等算法）
无需依赖整个数据；
泛化能力比较强；

缺点

当观测样本很多时，效率并不是很高；
对非线性问题没有通用解决方案，有时候很难找到一个合适的核函数；
对于核函数的高维映射解释力不强，尤其是径向基函数；
常规SVM只支持二分类；
对缺失数据敏感；

四.参考

SVM几种核函数的对比分析以及SVM算法的优缺点
线性判别准则与线性分类编程实践
基于jupyter notebook的python编程-----支持向量机学习二（SVM处理线性[鸢尾花数据集]和非线性数据集[月亮数据集]）