转置卷积(Transposed Convolution)
文章目录
- 前言
- 卷积操作
- 转置卷积操作
- Pytorch中的转置卷积参数
- Pytorch转置卷积实验
前言
转置卷积(Transposed Convolution) 在语义分割或者对抗神经网络(GAN)中比较常见,其主要作用就是做上采样(UpSampling)。在有些地方转置卷积又被称作fractionally-strided convolution或者deconvolution,但deconvolution具有误导性,不建议使用。对于转置卷积需要注意的是:
- 转置卷积不是卷积的逆运算、不是逆运算、不是逆运算(重要的事情说三遍)
- 转置卷积也是卷积
本文主要介绍转置卷积是如何计算的,关于转置卷积详细内容可以参考下面的文章:
- A guide to convolution arithmetic for deep learning
- https://blog.csdn.net/tsyccnh/article/details/87357447
不想看文章的可以看下我在bilibili上录的视频:
- https://www.bilibili.com/video/BV1mh411J7U4
卷积操作
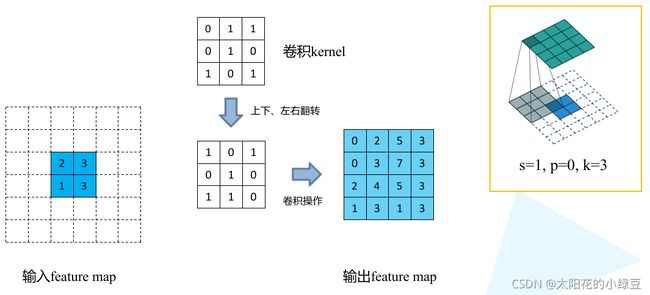
首先回顾下普通卷积,下图以stride=1,padding=0,kernel_size=3为例,假设输入特征图大小是4x4的(假设输入输出都是单通道),通过卷积后得到的特征图大小为2x2。一般使用卷积的情况中,要么特征图变小(stride > 1),要么保持不变(stride = 1),当然也可以通过四周padding让特征图变大但没有意义。关于卷积的详细介绍可以参考我之前的博文。

转置卷积操作
转置卷积刚刚说了,主要作用就是起到上采样的作用。但转置卷积不是卷积的逆运算(一般卷积操作是不可逆的),它只能恢复到原来的大小(shape)数值与原来不同。转置卷积的运算步骤可以归为以下几步:
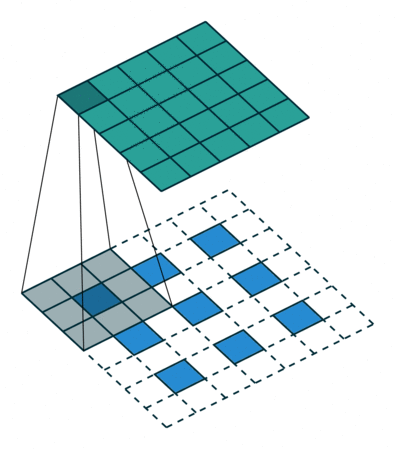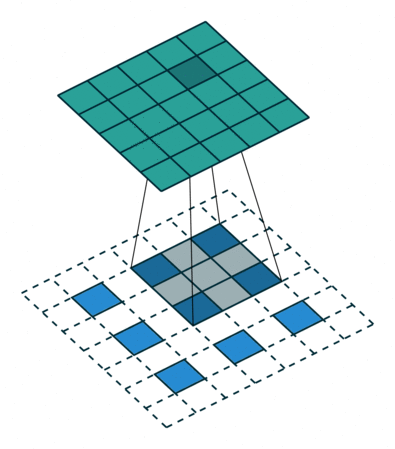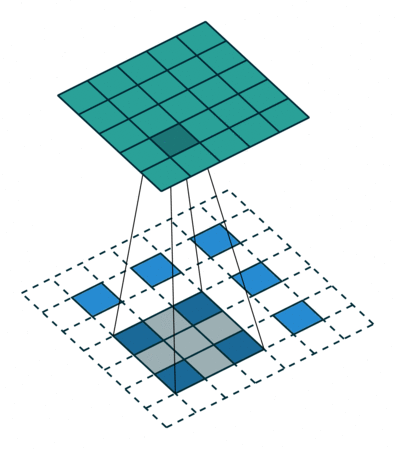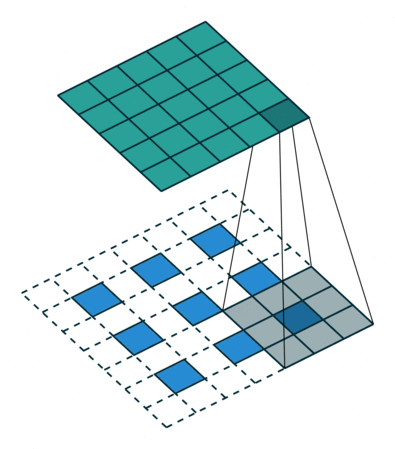
- 在输入特征图元素间填充s-1行、列0(其中s表示转置卷积的步距)
- 在输入特征图四周填充k-p-1行、列0(其中k表示转置卷积的kernel_size大小,p为转置卷积的padding,注意这里的padding和卷积操作中有些不同)
- 将卷积核参数上下、左右翻转
- 做正常卷积运算(填充0,步距1)
下面假设输入的特征图大小为2x2(假设输入输出都为单通道),通过转置卷积后得到4x4大小的特征图。这里使用的转置卷积核大小为k=3,stride=1,padding=0的情况(忽略偏执bias)。
- 首先在元素间填充s-1=0行、列0(等于0不用填充)
- 然后在特征图四周填充k-p-1=2行、列0
- 接着对卷积核参数进行上下、左右翻转
- 最后做正常卷积(填充0,步距1)
下图展示了转置卷积中不同s和p的情况:
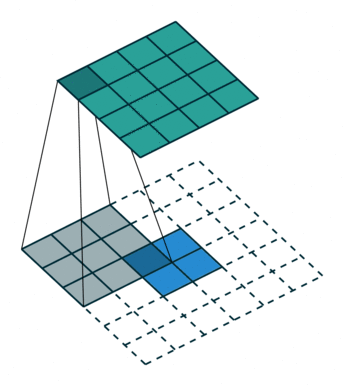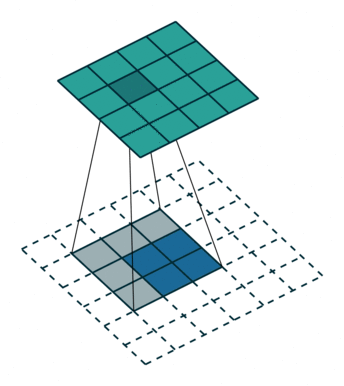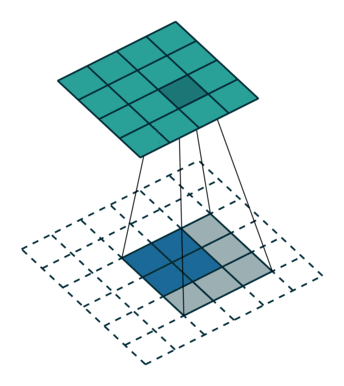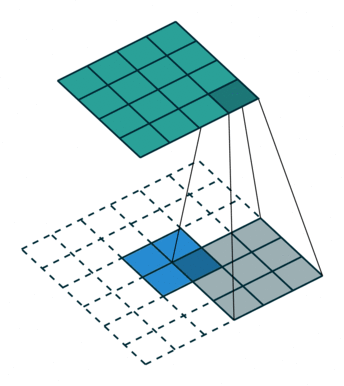
|
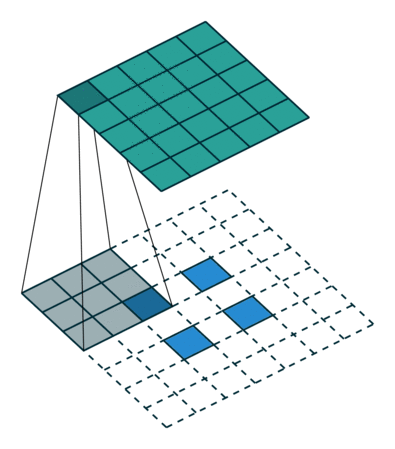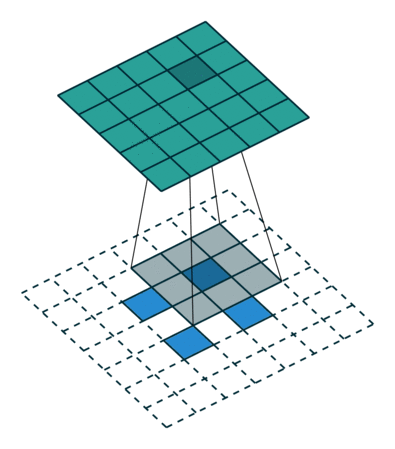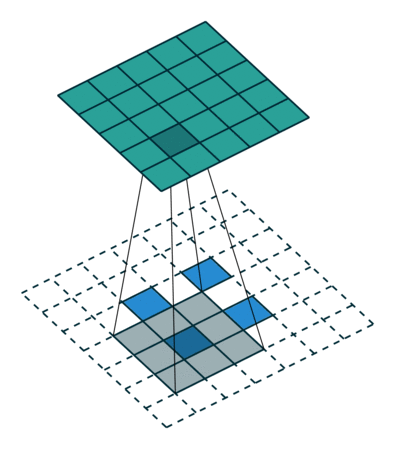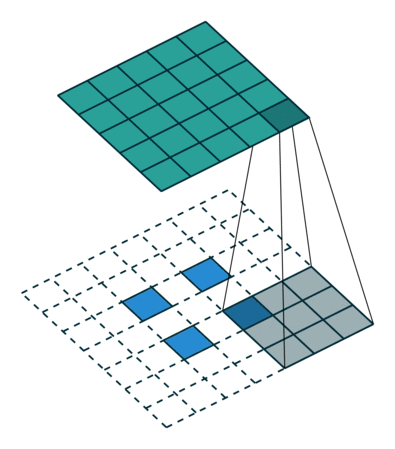
|
|
|
|
|
|
转置卷积操作后特征图的大小可以通过如下公式计算:
H o u t = ( H i n − 1 ) × s t r i d e [ 0 ] − 2 × p a d d i n g [ 0 ] + k e r n e l _ s i z e [ 0 ] W o u t = ( W i n − 1 ) × s t r i d e [ 1 ] − 2 × p a d d i n g [ 1 ] + k e r n e l _ s i z e [ 1 ] H_{out} =(H_{in}-1) \times {\rm stride[0]} - 2 \times {\rm padding[0]}+ {\rm kernel \_ size[0]} \\ W_{out} =(W_{in}-1) \times {\rm stride[1]} - 2 \times {\rm padding[1]}+ {\rm kernel \_ size[1]} Hout=(Hin−1)×stride[0]−2×padding[0]+kernel_size[0]Wout=(Win−1)×stride[1]−2×padding[1]+kernel_size[1]
其中stride[0]表示高度方向的stride,padding[0]表示高度方向的padding,kernel_size[0]表示高度方向的kernel_size,索引[1]都表示宽度方向上的。通过上面公式可以看出padding越大,输出的特征矩阵高、宽越小,你可以理解为正向卷积过程中进行了padding然后得到了特征图,现在使用转置卷积还原到原来高、宽后要把之前的padding减掉。
Pytorch中的转置卷积参数
pytorch官方关于转置卷积ConvTranspose2d的文档:https://pytorch.org/docs/stable/generated/torch.nn.ConvTranspose2d.html
官方原话:
Applies a 2D transposed convolution operator over an input image composed of several input planes.This module can be seen as the gradient of Conv2d with respect to its input. It is also known as a fractionally-strided convolution or a deconvolution (although it is not an actual deconvolution operation).
官方对转置卷积使用到的参数介绍:
 上面讲的例子中已经介绍了
上面讲的例子中已经介绍了in_channels, out_channels, kernel_size, stride, padding这几个参数了,在官方提供的方法中还有:
output_padding:在计算得到的输出特征图的高、宽方向各填充几行或列0(注意,这里只是在上下以及左右的一侧one side填充,并不是两侧都填充,有兴趣自己做个实验看下),默认为0不使用。groups:当使用到组卷积时才会用到的参数,默认为1即普通卷积。bias:是否使用偏执bias,默认为True使用。dilation:当使用到空洞卷积(膨胀卷积)时才会使用到的参数,默认为1即普通卷积。
输出特征图宽、高计算:
H o u t = ( H i n − 1 ) × s t r i d e [ 0 ] − 2 × p a d d i n g [ 0 ] + d i l a t i o n [ 0 ] × ( k e r n e l _ s i z e [ 0 ] − 1 ) + o u t p u t _ p a d d i n g [ 0 ] + 1 W o u t = ( W i n − 1 ) × s t r i d e [ 1 ] − 2 × p a d d i n g [ 1 ] + d i l a t i o n [ 1 ] × ( k e r n e l _ s i z e [ 1 ] − 1 ) + o u t p u t _ p a d d i n g [ 1 ] + 1 H_{out} =(H_{in}-1) \times {\rm stride[0]} - 2 \times {\rm padding[0]}+ {\rm dilation[0]} \times ({\rm kernel \_ size[0]}-1) + {\rm output\_padding[0]}+1 \\ W_{out} =(W_{in}-1) \times {\rm stride[1]} - 2 \times {\rm padding[1]}+ {\rm dilation[1]} \times ({\rm kernel \_ size[1]}-1) + {\rm output\_padding[1]}+1 Hout=(Hin−1)×stride[0]−2×padding[0]+dilation[0]×(kernel_size[0]−1)+output_padding[0]+1Wout=(Win−1)×stride[1]−2×padding[1]+dilation[1]×(kernel_size[1]−1)+output_padding[1]+1
Pytorch转置卷积实验
下面使用Pytorch框架来模拟s=1, p=0, k=3的转置卷积操作:

在代码中transposed_conv_official函数是使用官方的转置卷积进行计算,transposed_conv_self函数是按照上面讲的步骤自己对输入特征图进行填充并通过卷积得到的结果。
import torch
import torch.nn as nn
def transposed_conv_official():
feature_map = torch.as_tensor([[1, 0],
[2, 1]], dtype=torch.float32).reshape([1, 1, 2, 2])
print(feature_map)
trans_conv = nn.ConvTranspose2d(in_channels=1, out_channels=1,
kernel_size=3, stride=1, bias=False)
trans_conv.load_state_dict({
"weight": torch.as_tensor([[1, 0, 1],
[0, 1, 1],
[1, 0, 0]], dtype=torch.float32).reshape([1, 1, 3, 3])})
print(trans_conv.weight)
output = trans_conv(feature_map)
print(output)
def transposed_conv_self():
feature_map = torch.as_tensor([[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 2, 1, 0, 0],
[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0]], dtype=torch.float32).reshape([1, 1, 6, 6])
print(feature_map)
conv = nn.Conv2d(in_channels=1, out_channels=1,
kernel_size=3, stride=1, bias=False)
conv.load_state_dict({
"weight": torch.as_tensor([[0, 0, 1],
[1, 1, 0],
[1, 0, 1]], dtype=torch.float32).reshape([1, 1, 3, 3])})
print(conv.weight)
output = conv(feature_map)
print(output)
def main():
transposed_conv_official()
print("---------------")
transposed_conv_self()
if __name__ == '__main__':
main()
终端输出:
tensor([[[[1., 0.],
[2., 1.]]]])
Parameter containing:
tensor([[[[1., 0., 1.],
[0., 1., 1.],
[1., 0., 0.]]]], requires_grad=True)
tensor([[[[1., 0., 1., 0.],
[2., 2., 3., 1.],
[1., 2., 3., 1.],
[2., 1., 0., 0.]]]], grad_fn=)
---------------
tensor([[[[0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0.],
[0., 0., 1., 0., 0., 0.],
[0., 0., 2., 1., 0., 0.],
[0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0.]]]])
Parameter containing:
tensor([[[[0., 0., 1.],
[1., 1., 0.],
[1., 0., 1.]]]], requires_grad=True)
tensor([[[[1., 0., 1., 0.],
[2., 2., 3., 1.],
[1., 2., 3., 1.],
[2., 1., 0., 0.]]]], grad_fn=)
Process finished with exit code 0
通过对比能够发现,官方转置卷积的结果,和我们自己实现的转置卷积结果是一样的。对于其他的情况大家可以自己动手做做实验。