Artificial Intelligence-梯度下降法与线性回归
Artificial Intelligence
文章目录
- Artificial Intelligence
-
- 梯度下降法
-
- 基本概念
- 公式推导
- 基本梯度下降步骤
- 批量梯度下降(BGD)
- 随机梯度下降(SGD)
- 小批量梯度下降(MBGD)
- 线性回归
-
- 一元线性回归概念
- 原理引入
- 作业
-
- 实例一：单变量线性回归问题
梯度下降法
参考链接
基本概念
梯度下降法（gradient descent），又名最速下降法（steepest descent）是求解无约束最优化问题最常用的方法，它是一种迭代方法，每一步主要的操作是求解目标函数的梯度向量，将当前位置的负梯度方向作为搜索方向（因为在该方向上目标函数下降最快，这也是最速下降法名称的由来）。
梯度下降，其实就是一个公式：
公式推导
基本梯度下降步骤
步骤：
η为学习率，ε为收敛条件。梯度下降法属于机器学习，本质为：不断迭代判断是否满足条件，会用到循环语句。
Created with Raphaël 2.2.0 首先设定一个较小的正数m,n; 求当前位置处的各个偏导数; 修改当前函数的参数值; 参数变化量小于n 求得极小值 结束框 回退迭代 yes no
批量梯度下降(BGD)
Batch gradient descent:：批量梯度下降算法(BGD)，其需要计算整个训练集的梯度，即：
其中η为学习率，用来控制更新的“力度”/“步长”。
- 优点：
对于凸目标函数，可以保证全局最优； 对于非凸目标函数，可以保证一个局部最优。
- 缺点：
速度慢; 数据量大时不可行; 无法在线优化(即无法处理动态产生的新样本)。
代码实现
#引库
#引入matplotlib库,用于画图
import matplotlib.pyplot as plt
from math import pow
#图片嵌入jupyter
#matplotlib inline
#为了便于取用数据,我们将数据分为x,y,在直角坐标系中(x,y)是点
x = [1,2,3,4,5,6]
y = [13,14,20,21,25,30]
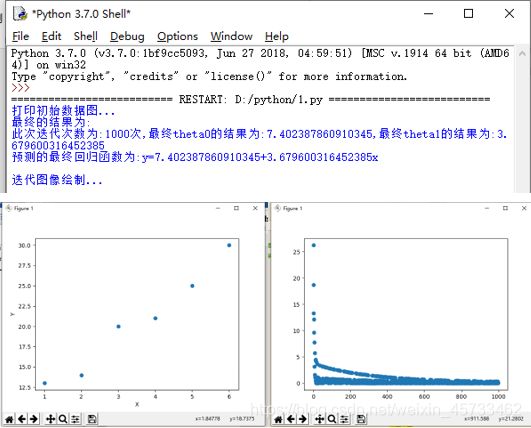
print("打印初始数据图...")
plt.scatter(x,y)
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
#超参数设定
alpha = 0.01#学习率/步长
theta0 = 0#θ0
theta1 = 0#θ1
epsilon = 0.001#误差
m = len(x)
count = 0
loss = []
for time in range(1000):
count += 1
#求偏导theta0和theta1的结果
temp0 = 0#J(θ)对θ0求导的结果
temp1 = 0#J(θ)对θ1求导的结果
diss = 0
for i in range(m):
temp0 += (theta0+theta1*x[i]-y[i])/m
temp1 += ((theta0+theta1*x[i]-y[i])/m)*x[i]
#更新theta0和theta1
for i in range(m):
theta0 = theta0 - alpha*((theta0+theta1*x[i]-y[i])/m)
theta1 = theta1 - alpha*((theta0+theta1*x[i]-y[i])/m)*x[i]
#求损失函数J(θ)
for i in range(m):
diss = diss + 0.5*(1/m)*pow((theta0+theta1*x[i]-y[i]),2)
loss.append(diss)
#看是否满足条件
'''
if diss<=epsilon:
break
else:
continue
'''
print("最终的结果为:")
print("此次迭代次数为:{}次,最终theta0的结果为:{},最终theta1的结果为:{}".format(count,theta0,theta1))
print("预测的最终回归函数为:y={}+{}x\n".format(theta0,theta1))
print("迭代图像绘制...")
plt.scatter(range(count),loss)
plt.show()
运行结果
随机梯度下降(SGD)
Stochastic gradient descent：随机梯度下降算法(SGD)，仅计算某个样本的梯度，即针对某一个训练样本 xi及其label yi更新参数：
逐步减小学习率，SGD表现得同BGD很相似，最后都可以有不错的收敛。
- 优点：
更新频次快，优化速度更快; 可以在线优化(可以无法处理动态产生的新样本)；一定的随机性导致有几率跳出局部最优(随机性来自于用一个样本的梯度去代替整体样本的梯度)。
- 缺点：
随机性可能导致收敛复杂化，即使到达最优点仍然会进行过度优化，因此SGD得优化过程相比BGD充满动荡。
代码实现
#引库
#引入matplotlib库,用于画图
import matplotlib.pyplot as plt
from math import pow
import numpy as np
#图片嵌入jupyter
#matplotlib inline
#为了便于取用数据,我们将数据分为x,y,在直角坐标系中(x,y)是点
x = [1,2,3,4,5,6]
y = [13,14,20,21,25,30]
print("打印初始数据图...")
plt.scatter(x,y)
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
#超参数设定
alpha = 0.01#学习率/步长
theta0 = 0#θ0
theta1 = 0#θ1
epsilon = 0.001#误差
m = len(x)
count = 0
loss = []
for time in range(1000):
count += 1
diss = 0
#求偏导theta0和theta1的结果
temp0 = 0#J(θ)对θ0求导的结果
temp1 = 0#J(θ)对θ1求导的结果
for i in range(m):
temp0 += (theta0+theta1*x[i]-y[i])/m
temp1 += ((theta0+theta1*x[i]-y[i])/m)*x[i]
#更新theta0和theta1
for i in range(m):
theta0 = theta0 - alpha*((theta0+theta1*x[i]-y[i])/m)
theta1 = theta1 - alpha*((theta0+theta1*x[i]-y[i])/m)*x[i]
#求损失函数J(θ)
rand_i = np.random.randint(0,m)
diss += 0.5*(1/m)*pow((theta0+theta1*x[rand_i]-y[rand_i]),2)
loss.append(diss)
#看是否满足条件
'''
if diss<=epsilon:
break
else:
continue
'''
print("最终的结果为:")
print("此次迭代次数为:{}次,最终theta0的结果为:{},最终theta1的结果为:{}".format(count,theta0,theta1))
print("预测的最终回归函数为:y={}+{}x\n".format(theta0,theta1))
print("迭代图像绘制...")
plt.scatter(range(count),loss)
plt.show()
运行结果
小批量梯度下降(MBGD)
Mini-batch gradient descent：小批量梯度下降算法(MBGD)，计算包含n个样本的mini-batch的梯度：
MBGD是训练神经网络最常用的优化方法。
- 优点：
参数更新时的动荡变小，收敛过程更稳定，降低收敛难度；可以利用现有的线性代数库高效的计算多个样本的梯度。
代码实现
#引库
#引入matplotlib库,用于画图
import matplotlib.pyplot as plt
from math import pow
import numpy as np
#图片嵌入jupyter
#matplotlib inline
#为了便于取用数据,我们将数据分为x,y,在直角坐标系中(x,y)是点
x = [1,2,3,4,5,6]
y = [13,14,20,21,25,30]
print("打印初始数据图...")
plt.scatter(x,y)
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
#超参数设定
alpha = 0.01#学习率/步长
theta0 = 0#θ0
theta1 = 0#θ1
epsilon = 0.001#误差
diss = 0#损失函数
m = len(x)
count = 0
loss = []
for time in range(1000):
count += 1
diss = 0
#求偏导theta0和theta1的结果
temp0 = 0#J(θ)对θ0求导的结果
temp1 = 0#J(θ)对θ1求导的结果
for i in range(m):
temp0 += (theta0+theta1*x[i]-y[i])/m
temp1 += ((theta0+theta1*x[i]-y[i])/m)*x[i]
#更新theta0和theta1
for i in range(m):
theta0 = theta0 - alpha*((theta0+theta1*x[i]-y[i])/m)
theta1 = theta1 - alpha*((theta0+theta1*x[i]-y[i])/m)*x[i]
#求损失函数J(θ)
result = []
for i in range(3):
rand_i = np.random.randint(0,m)
result.append(rand_i)
for j in result:
diss += 0.5*(1/m)*pow((theta0+theta1*x[j]-y[j]),2)
loss.append(diss)
#看是否满足条件
'''
if diss<=epsilon:
break
else:
continue
'''
print("最终的结果为:")
print("此次迭代次数为:{}次,最终theta0的结果为:{},最终theta1的结果为:{}".format(count,theta0,theta1))
print("预测的最终回归函数为:y={}+{}x\n".format(theta0,theta1))
print("迭代图像绘制...")
plt.scatter(range(count),loss)
plt.show()
运行结果
线性回归
参考链接1
参考链接2
一元线性回归概念
一元线性回归其实就是从一堆训练集中去算出一条直线，使数据集到直线之间的距离差最小。
最简单的模型如图所示：
下列2个模型都是线性回归模型，即便右图中的线看起来并不像直线。
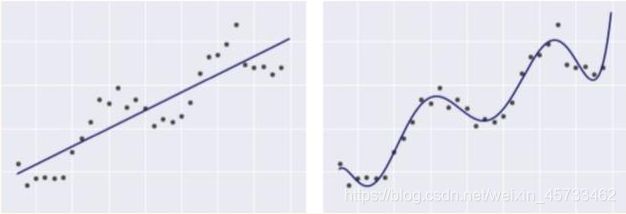
原理引入
唯一特征X，共有m = 500个数据数量，Y是实际结果，要从中找到一条直线，使数据集到直线之间的距离差最小，如下图所示：
作业
实例一：单变量线性回归问题
房屋价格与面积（数据在下面表格中）
| 序号 | 面积 | 价格 |
|---|---|---|
| 1 | 150 | 6450 |
| 2 | 200 | 7450 |
| 3 | 250 | 8450 |
| 4 | 300 | 9450 |
| 5 | 350 | 11450 |
| 6 | 400 | 15450 |
| 7 | 600 | 18450 |
使用梯度下降求解线性回归
要求：
（1）对关键代码进行注释；
（2）把每次迭代计算出来的theta0 ，theta1 画出来；
（3）分别用随机梯度和批量梯度实现，并在同一个图形中进行对比（颜色不同）。
代码实现
#引入matplotlib库,用于画图
import matplotlib.pyplot as plt
import random
import matplotlib
#建立直角坐标系（x,y）
x = [150,200,250,300,350,400,600]
y = [6450,7450,8450,9450,11450,15450,18450]
#步长
alpha = 0.00001
#计算样本个数，即m=7
m = len(x)
#初始化参数的值，拟合函数为 y=theta0+theta1*x，p为批量，s为随机
ptheta0 = 0
ptheta1 = 0
stheta1=0
stheta0=0
#误差
error0=0
error1=0
#退出迭代的两次误差差值的阈值
epsilon=0.000001
#批量梯度下降BGD
def p(x):
return ptheta1*x+ptheta0
#随机梯度下降SGD
def s(x):
return stheta1*x+stheta0
#开始迭代批量梯度
presult0 = []
presult1 = []
while True:
diff = [0,0]
# 梯度下降
for i in range(m):
diff[0] += p(x[i]) - y[i] # 对theta0求导
diff[1] += (p(x[i]) - y[i]) * x[i] # 对theta1求导
ptheta0 = ptheta0 - alpha / m * diff[0]
ptheta1 = ptheta1 - alpha / m * diff[1]
presult0.append(ptheta0)
presult1.append(ptheta1)
error1 = 0
# 计算两次迭代的误差的差值，小于阈值则退出迭代，输出拟合结果
for i in range(len(x)):
error1 += (y[i] - (ptheta0 + ptheta1 * x[i])) ** 2 / 2
if abs(error1 - error0) < epsilon:
break
else:
error0 = error1
#开始迭代随机梯度
sresult0 = []
sresult1 = []
for j in range(5000):
diff = [0, 0]
# 梯度下降
i = random.randint(0, m - 1)
diff[0] += s(x[i]) - y[i] # 对theta0求导
diff[1] += (s(x[i]) - y[i]) * x[i] # 对theta1求导
stheta0 = stheta0 - alpha / m * diff[0]
stheta1 = stheta1 - alpha / m * diff[1]
sresult0.append(stheta0)
sresult1.append(stheta1)
error1 = 0
# 计算两次迭代的误差的差值，小于阈值则退出迭代，输出拟合结果
for k in range(len(x)):
error1 += (y[i] - (stheta0 + stheta1 * x[i])) ** 2 / 2
if abs(error1 - error0) < epsilon:
break
else:
error0 = error1
#结果
print(ptheta1,ptheta0)
print(stheta1,stheta0)
#画图
a=len(presult0)
C=len(presult1)
b=range(a)
c=range(C)
plt.plot(b,presult0)
plt.xlabel("Runs")
plt.ylabel("theta0")
plt.show()
plt.plot(c,presult1)
plt.xlabel("Runs")
plt.ylabel("theta1")
plt.show()
a1=len(sresult0)
C1=len(sresult1)
b1=range(a1)
c1=range(C1)
plt.plot(b1,sresult0)
plt.xlabel("Runs")
plt.ylabel("theta0")
plt.show()
plt.plot(c1,sresult1)
plt.xlabel("运行次数")
plt.ylabel("theta1")
plt.show()
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
plt.plot(x,[p(x) for x in x],label='批量梯度')
plt.plot(x,[s(x) for x in x],label='随机梯度')
plt.plot(x,y,'bo',label='数据')
plt.legend()
plt.show()
运行结果：
（1）批量梯度：
theta1=28.778604659732547
theta0=1771.0428917695647
theta0随运行次数的变化见上图
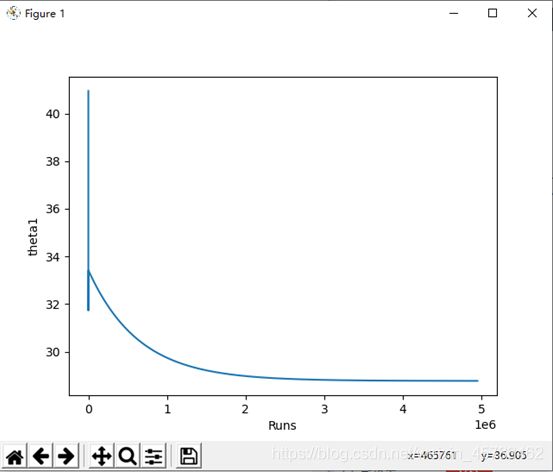
theta1随运行次数的变化见上图
（2）批量梯度：
theta1=33.71739545116426
theta0=2.0564426533254134
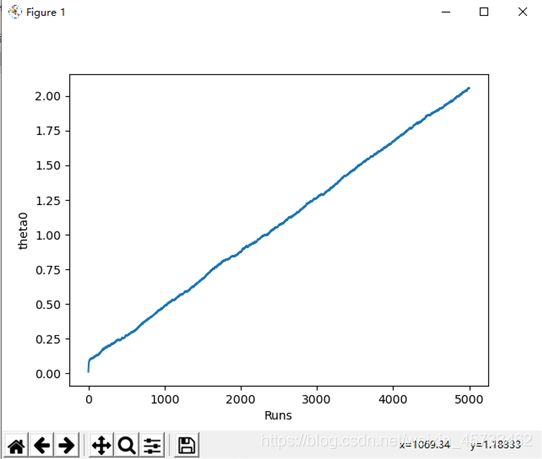
theta0随运行次数的变化见上图
theta1随运行次数的变化见上图
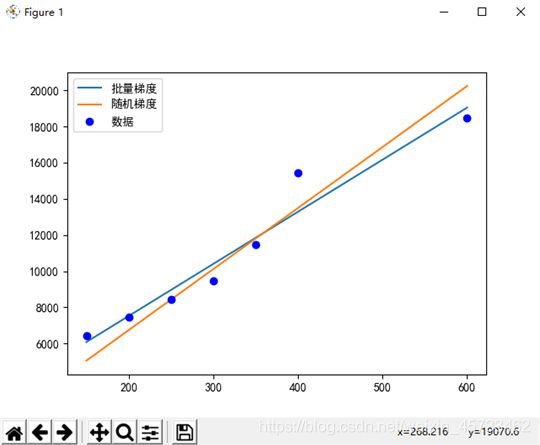
结果对比见上图
总结
我想，大部分人刚接触到这块知识，都是觉得好难，头秃@~~@。其实学后在回头想想，还行吧，这一章节主要是理解梯度下降的本质、公式的推导、批量梯度下降和随机梯度下降。（小批量梯度下降不太常用）
代码的话（以房屋价格与面积的问题为例），其实就是两种梯度下降的合成，代码中除BGD和SGD的关键代码不同，其余的还是很相似的。还有一点就是，matplotlib库函数的一些操作，如果不会这个，那就没办法画图像了。