鸽巢原理详解

鸽巢原理

假设我们有 10 只鸽子，但只有 9 个鸽笼可以放入它们。由于我们的鸽子比鸽笼多，因此至少其中一个洞必须至少有 2 只鸽子。 这就是鸽巢原理。 每当我们要放入孔中的物品多于孔时，至少一个孔必须包含不止一件物品。

假设鸽子的数为n，鸽笼的个数为k，那么上述原理转换下就是： 鸽巢原理

❝

假设你有 k 个鸽笼和 n 只鸽子要放在里面。 如果 n > k (鸽子数 > 鸽笼数) 那么至少一个鸽舍包含至少两只鸽子。

❞

其中，鸽子通常是数字、物体乃至一个对象，而鸽笼则是存储数组、物体或者对象的一个容器。

证明

我们第一反应是，这不是显而易见的么？还需要证明？

想象一下，一群鸽子被塞进了许多抽屉。 只要鸽子的数量超过抽屉的数量，至少一个抽屉会包含两只鸽子。 请注意，即使在最平等的情况下，每个抽屉都有一只鸽子，但最后仍有剩余的鸽子需要放入其中一个已经装满的抽屉，从而实现原则。 如果鸽子是按概率分布的，当然有些抽屉里可能会有超过两只鸽子。

在一般情况下，如果将 n 个对象放入 m 个容器中，则：

• 如果n < m,则有部分容器是空的
• 如果 n > m, 则有部分容器至少有两个对象 那么转换成公式就是：

n = (r - 1)m + 1

或者

r = [(n - 1) / m] + 1 = ROUNDUP(n / m)

其中：

❝

n 为鸽子或者对象的数量 m 为鸽巢或者容器的数量 r 为容器或者鸽巢中 最多的对象或者鸽子的数量

❞

假设 n < m 并且存在从 Nm = {1, ..., m} 到 Nn = {1, ..., n} 的函数 f。 这意味着，对于每个 k∈Nm，都有一个元素 f(k)∈Nn。 此外，假设 Nn 中没有任何元素与 Nm 中的一个以上元素相关联。 换句话说，i,j∈Nm 和 i≠j 意味着 f(i)≠f(j)。 这恰恰意味着 f(Nm) 是 Nn 的子集，使得 m = |f(Nm)| = |Nm| ≤ |Nn| = n。 但这与我们的假设 n

应用

以leetcode第442题为例

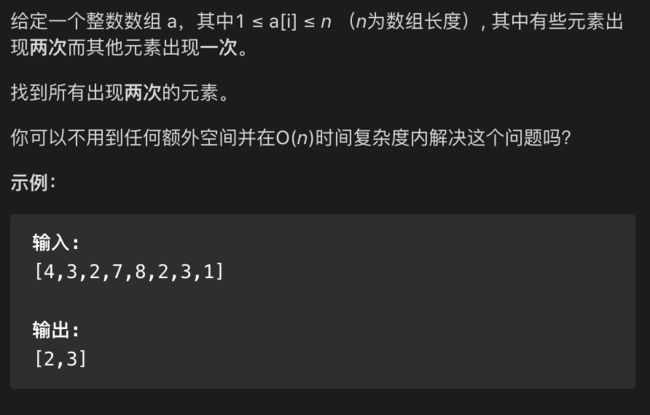
分析：

❝

n个巢， n+1只鸽子，每个鸽子进一个巢，那种总会剩下一个鸽子无家可归； 在此问题中我们假设数字的下标为鸽巢，下标对应的值为鸽子编号。 经过一次遍历让鸽子（回到鸽子编号-1的巢里）回家，最终发现无家可归的鸽子，和没有鸽子的巢。

❞

代码实现：

vector findDisappearedNumbers(vector& nums) {
        int n=nums.size();
        for(int i=0;i        {
            while(nums[i]!=nums[nums[i]-1])
                swap(nums[i],nums[nums[i]-1]);
        }     
        vector res;
        for(int i=0;i        {
            if(nums[i]!=i+1)
                res.push_back(nums[i]);
        }   
        return res;
    }

---

专注于高性能架构探索与开发，关注公众号【高性能架构探索】，一起进步