【20210821 corCTF YauzaCTF】Crypto&OSINT方向部分WP
熟悉的界面,赛后复现,前两天有祥云杯
看到好多师傅都给全a了
文章目录
- corCTF
-
- Crypto-fibinary
- Crypto-4096
- Crypto-dividing_secrets
- Crypto-supercomputer
- Crypto-babyrsa
- Crypto-babypad(unsolved)
- Crypto-babyrand(recuring)
- Crypto-LCG_k(unsolved)
- YauzaCTF
-
- Crypto-Sharing secrets
- Crypto-Knapsack(unsolved)
- OSINT-Stolen Capitalism(unsolved)
- OSINT-Get in touch(recuring)
corCTF
Crypto-fibinary
fib = [1, 1]
for i in range(2, 11):
fib.append(fib[i - 1] + fib[i - 2])
def c2f(c):
n = ord(c)
b = ''
for i in range(10, -1, -1):
if n >= fib[i]:
n -= fib[i]
b += '1'
else:
b += '0'
return b
flag = open('flag.txt', 'r').read()
enc = ''
for c in flag:
enc += c2f(c) + ' '
with open('flag.enc', 'w') as f:
f.write(enc.strip())
10000100100 10010000010 10010001010 10000100100 10010010010 10001000000 10100000000 10000100010 00101010000 10010010000 00101001010 10000101000 10000010010 00101010000 10010000000 10000101000 10000010010 10001000000 00101000100 10000100010 10010000100 00010101010 00101000100 00101000100 00101001010 10000101000 10100000100 00000100100
fib = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]
enc = '10000100100 10010000010 10010001010 10000100100 10010010010 10001000000 10100000000 10000100010 00101010000 10010010000 00101001010 10000101000 10000010010 00101010000 10010000000 10000101000 10000010010 10001000000 00101000100 10000100010 10010000100 00010101010 00101000100 00101000100 00101001010 10000101000 10100000100 00000100100'
enc = enc.split(' ')
flag = ''
for i in enc:
n = 0
for j in range(len(fib)):
if i[j] == '1':
n += fib[len(fib)-j-1]
flag += chr(n)
print(flag)
corctf{b4s3d_4nd_f1bp!113d}
Crypto-4096
from Crypto.Util.number import getPrime, bytes_to_long
from private import flag
def prod(lst):
ret = 1
for num in lst:
ret *= num
return ret
m = bytes_to_long(flag)
primes = [getPrime(32) for _ in range(128)]
n = prod(primes)
e = 65537
print(n)
print(pow(m, e, n))
#!/usr/bin/env sage
# -*- coding: utf-8 -*-
from Crypto.Util.number import long_to_bytes
from gmpy2 import invert
n = 50630448182626893495464810670525602771527685838257974610483435332349728792396826591558947027657819590790590829841808151825744184405725893984330719835572507419517069974612006826542638447886105625739026433810851259760829112944769101557865474935245672310638931107468523492780934936765177674292815155262435831801499197874311121773797041186075024766460977392150443756520782067581277504082923534736776769428755807994035936082391356053079235986552374148782993815118221184577434597115748782910244569004818550079464590913826457003648367784164127206743005342001738754989548942975587267990706541155643222851974488533666334645686774107285018775831028090338485586011974337654011592698463713316522811656340001557779270632991105803230612916547576906583473846558419296181503108603192226769399675726201078322763163049259981181392937623116600712403297821389573627700886912737873588300406211047759637045071918185425658854059386338495534747471846997768166929630988406668430381834420429162324755162023168406793544828390933856260762963763336528787421503582319435368755435181752783296341241853932276334886271511786779019664786845658323166852266264286516275919963650402345264649287569303300048733672208950281055894539145902913252578285197293
c = 15640629897212089539145769625632189125456455778939633021487666539864477884226491831177051620671080345905237001384943044362508550274499601386018436774667054082051013986880044122234840762034425906802733285008515019104201964058459074727958015931524254616901569333808897189148422139163755426336008738228206905929505993240834181441728434782721945966055987934053102520300610949003828413057299830995512963516437591775582556040505553674525293788223483574494286570201177694289787659662521910225641898762643794474678297891552856073420478752076393386273627970575228665003851968484998550564390747988844710818619836079384152470450659391941581654509659766292902961171668168368723759124230712832393447719252348647172524453163783833358048230752476923663730556409340711188698221222770394308685941050292404627088273158846156984693358388590950279445736394513497524120008211955634017212917792675498853686681402944487402749561864649175474956913910853930952329280207751998559039169086898605565528308806524495500398924972480453453358088625940892246551961178561037313833306804342494449584581485895266308393917067830433039476096285467849735814999851855709235986958845331235439845410800486470278105793922000390078444089105955677711315740050638
e = 0x10001
phi = 1
for i in factor(n):
phi *= i[0]-1
print(long_to_bytes(pow(c, invert(e, phi), n)))
corctf{to0_m4ny_pr1m3s55_63aeea37a6b3b22f}
Crypto-dividing_secrets
from Crypto.Util.number import bytes_to_long, getStrongPrime
from random import randrange
from secret import flag
LIMIT = 64
def gen():
p = getStrongPrime(512)
g = randrange(1, p)
return g, p
def main():
g, p = gen()
print("g:", str(g))
print("p:", str(p))
x = bytes_to_long(flag)
enc = pow(g, x, p)
print("encrypted flag:", str(enc))
ctr = 0
while ctr < LIMIT:
try:
div = int(input("give me a number> "))
print(pow(g, x // div, p))
ctr += 1
except:
print("whoops..")
return
print("no more tries left... bye")
main()
以为我没有打祥云杯吗,可笑
直接二分法逼近
# nc crypto.be.ax 6000
from Crypto.Util.number import bytes_to_long, long_to_bytes
from pwn import *
import sys
# context.log_level = 'debug'
l = 10 ** 153
r = 10 ** 154
while 1:
try:
sh = remote('crypto.be.ax', 6000)
except:
continue
sh.recvuntil(b'g: ')
g = int(sh.recvline())
sh.recvuntil(b'p: ')
p = int(sh.recvline())
sh.recvuntil(b'encrypted flag: ')
try:
while l < r:
sh.recvuntil(b'give me a number>')
mid = (l + r) // 2
sh.sendline(str(mid).encode())
t = sh.recvline()
if b'corctf{' in long_to_bytes(mid):
print(long_to_bytes(mid))
if int(t.decode()) == 1:
r = mid
else:
l = mid
except:
sh.close()
corctf{qu4drat1c_r3s1due_0r_n0t_1s_7h3_qu3st1on8852042051e57492}
但是看到flag,说是二次剩余,又是非预期?之前做InCTF的Gold_digger时,做到GM同态加密,其中就有用到二次剩余,二次非剩余
emmmmm非预期就非预期吧
Crypto-supercomputer
from Crypto.Util.number import getPrime, long_to_bytes
from pwn import *
import random, binascii
flag = open('flag.txt').read()
def v(p, k):
ans = 0
while k % p == 0:
k /= p
ans += 1
return ans
p, q, r = getPrime(2048), getPrime(2048), getPrime(2048)
print(p, q, r)
n = pow(p, q) * r
a1 = random.randint(0, n)
a2 = n - a1
assert a1 % p != 0 and a2 % p != 0
t = pow(a1, n) + pow(a2, n)
print(binascii.hexlify(xor(flag, long_to_bytes(v(p, t)))))
简单的二项式展开,展到最后把指数最小的n给除完了,a1暴露出来,由于a1不是p的倍数,所以函数v中的循环条件不满足,循环结束
from pwn import xor
from Crypto.Util.number import long_to_bytes
from binascii import unhexlify
p = 20936670545375210972091706288423179494163425035286134775773514440843943493090886819895346572945288304582498268271507942037581752184819846906869395551921930704321251130746547888224652316226957634541702883599286787839982090615950687496752999645558331533314682453610929822041558882012483238149288762974740347582024050756443700107245858419316423473568526347559377124536218894368962796664914408327949348396038507355935608178392088898784474582354438590711083089253977971653913217304360725716982473871023235180637867588860233011122300656470435644430602412710493441965130162664981423496370539240693045312454250776393871037539
q = 19872523115298089612152987731023453644084277408261276810219001288407280019889227914287760742936580023163800626696116882213533508813201232707621762739857924392306902336092739272758773377952936022982446120177174082641600741522817135305633293579042208014735900229922142564590095968054337719254632703676737069746032384348392244892496672044899073391936273280270753785076044108870166304800552404013519058026991588856235381264192387525832530187004466616791531223421070547342377071358044704265893255021275811622959301157507095984825182110574434699593886509171425701861331576642311553357835312334349976576969220483604368671153
r = 18342695102288954165224207958150786487860883752676419020596228714991017967256173183699487408637445601341687447489432163178271335469203559084363600703497940503946684342504933131623546315643648637992201226732630680112575643707020017139390225257319697353426087369722671485915571962910153169877358046375850132351117527591675467417925944135644417622440847857598273517926844822766083086147088819776687612745404553608100705862181700054385028096749375873889019995159762301115707945396140178370414857973922007665218670792403129624089144668480280115489465764431016721028424152163659378120333071194425845370101841510224643446231
c = b'6255a505b969be8175a5c578fd6e856ecd85faa1a22fdf38d2d11851211676fd3047ed12c4027e66ed2173495877180e3d49a387b74701fbbbdce00a2248c7812b157626c95e7cf5727ee90cc9a6a98d84ee50f106b11245d65b87a27bbd7ab94b0d82eeb6e49e81249ae880c150ff87d8da701e9d317932fa2b27b64eb894a112d942d7d269478a6c120be885f3fbd065c38e70498c2f294b47bb08da09fb63c05070248079fe4311c9821dd8d3a08b15f13cdb0b7a8d406790c4796e0218851b496a11bf1ad7575be6d9999d5f1c73080d724c66a116f865ffcd3048be5d59dae55a4a063629d30429765733521702ec36d3f111b015934d15d620ad0e35ee56'
print(xor(unhexlify(c), long_to_bytes(2*q)))
corctf{1_b3t_y0u_d1dnt_4ctu411y_d0_th3_m4th_d1d_y0u?}
其实是个变种,la佬的博客上有
Crypto-babyrsa
willwam845师傅出的题
from Crypto.Util.number import bytes_to_long
n = 73542616560647877565544036788738025202939381425158737721544398356851787401183516163221837013929559568993844046804187977705376289108065126883603562904941748653607836358267359664041064708762154474786168204628181667371305788303624396903323216279110685399145476916585122917284319282272004045859138239853037072761
e = 0x10001
flag = bytes_to_long(open("flag.txt", "rb").read())
print(f"n = {
n}")
print(f"e = {
e}")
print(f"ct = {
pow(flag, e, n)}")
print("""
Transcription of image:
735426165606478775655440367887380252029393814251587377215443983568517874011835161632
289108065126883603562904941748653607836358267359664041064708762154474786168204628181
9145476916585122917284319282272004045859138239853037072761
108294440701045353595867242719660522374526250640690193563048263854806748525172379331
341078269246532299656864881223
679098724593514422867704492870375465007225641192338424726642090768164214390632598250
39563231146143146482074105407
(n, p, q)
""")
n = 73542616560647877565544036788738025202939381425158737721544398356851787401183516163221837013929559568993844046804187977705376289108065126883603562904941748653607836358267359664041064708762154474786168204628181667371305788303624396903323216279110685399145476916585122917284319282272004045859138239853037072761
e = 65537
ct = 2657054880167593054409755786316190176139048369036893368834913798649283717358246457720021168590230987384201961744917278479195838455294205306264398417522071058105245210332964380113841646083317786151272874874267948107036095666198197073147087762030842808562672646078089825632314457231611278451324232095496184838
Transcription of image:
735426165606478775655440367887380252029393814251587377215443983568517874011835161632
289108065126883603562904941748653607836358267359664041064708762154474786168204628181
9145476916585122917284319282272004045859138239853037072761
108294440701045353595867242719660522374526250640690193563048263854806748525172379331
341078269246532299656864881223
679098724593514422867704492870375465007225641192338424726642090768164214390632598250
39563231146143146482074105407
(n, p, q)
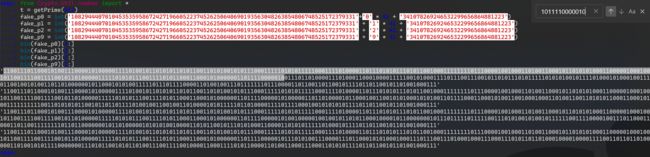
不愧是willwam845师傅,出的很有水平,截了discord上的一张图,利用截图截不全构造了已知p,q高位的攻击
和一般的CopperSmith已知p的高位攻击略不同,并没有直接给出p真正的高位,只是截取了10进制前几位,因为有n很容易就能知道p缺的十进制数的位数是41,所以要转换一下二进制才是,像图中我选中的二进制部分,这四个数都有,这才是真正的高位
这就和我们所熟悉的一样了吗
网上有一些脚本,针对RSA已知p高位的,至少是p位数的 1 2 \frac{1}{2} 21,还说如果位数不够需要爆破;不是很理解这个 1 2 \frac{1}{2} 21,按道理来说275位应该早超多 1 2 \frac{1}{2} 21位了呀,我多加了3位十六进制的爆破才出来
而且他这里也是至少知道576位,也是超过一半512的,不懂,评论区万能的师傅能告诉我吗?或者是和Copper格的原理有关,后续再研究
#!/usr/bin/env sage
# -*- coding: utf-8 -*-
from Crypto.Util.number import long_to_bytes
from gmpy2 import invert
# 21837013929559568993844046804187977705376341078269246532299656864881223
# 341078269246532299656864881223
n = 73542616560647877565544036788738025202939381425158737721544398356851787401183516163221837013929559568993844046804187977705376289108065126883603562904941748653607836358267359664041064708762154474786168204628181667371305788303624396903323216279110685399145476916585122917284319282272004045859138239853037072761
c = 2657054880167593054409755786316190176139048369036893368834913798649283717358246457720021168590230987384201961744917278479195838455294205306264398417522071058105245210332964380113841646083317786151272874874267948107036095666198197073147087762030842808562672646078089825632314457231611278451324232095496184838
e = 0x10001
# 已知P的高位,最后面12位二进制,也就是3位十六进制要参与爆破,所以要用000补充
# fakep>>237<<237转十六进制末尾填充3个0
p = 0x67629c283d2d5acd4ae3eaf8f43757591fee1234c5aa3044b3cf2d07d5cf58c503782000
# P原本的位数
pbits = 512
# 要爆破的12位二进制数,为2**12==4096,表示0~4096
for i in range(0,4096):
p4 = p
p4 = p4 + int(hex(i),16)
kbits = pbits - p4.nbits()
p4 = p4 << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = x + p4
roots = f.small_roots(X = 2^kbits, beta = 0.4)
# 经过以上一些函数处理后,n和p已经被转化为10进制
if roots:
p= p4 + int(roots[0])
assert n % p == 0
q = n // p
print(long_to_bytes(pow(c, invert(e, (p-1)*(q-1)), n)))
corctf{1_w4s_f0rc3d_t0_wr1t3_ch4ll5_4nd_1_h4d_n0_g00d_1d345_pl5_n0_bully_;-;}
Crypto-babypad(unsolved)
from Crypto.Cipher import AES
from Crypto.Util import Counter
from Crypto.Util.Padding import pad, unpad
from Crypto.Util.number import bytes_to_long
import os
flag = open("/challenge/flag.txt").read().encode()
key = os.urandom(16)
def encrypt(pt):
iv = os.urandom(16)
ctr = Counter.new(128, initial_value=bytes_to_long(iv))
cipher = AES.new(key, AES.MODE_CTR, counter=ctr)
return iv + cipher.encrypt(pad(pt, 16))
def decrypt(ct):
try:
iv = ct[:16]
ct = ct[16:]
ctr = Counter.new(128, initial_value=bytes_to_long(iv))
cipher = AES.new(key, AES.MODE_CTR, counter=ctr)
pt = cipher.decrypt(ct)
unpad(pt, 16)
return 1
except Exception as e:
return 0
def main():
print(encrypt(flag).hex())
while True:
try:
print(decrypt(bytes.fromhex(input("> "))))
except Exception as e:
pass
main()
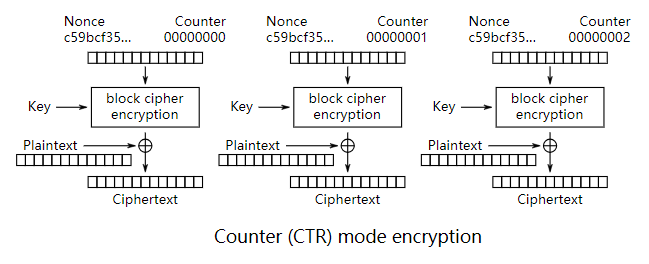
AES的CTR模式(计数器模式),大致的加密流程如下
解密就是将Ciphertext和Plaintext互换位置,Key和Nonce不变
而我们从密文看,似乎flag小于16字节,也就是在32个字符以内,所以填充之后,就只有一组;除了密文和iv,其他具体的信息我们都得不到了,只有成功解密和失败解密回显的区别,看来要爆破
没什么思路,不知道是从流程下手,还是有针对CTR的攻击手法,题目提示pad
这个pad函数很有意思,不仅将明文填充成长度为16字节的倍数,而且根据剩余多少位补充不同的字节,比如
好在CTFTIME有师傅贴了WP,去舔一波
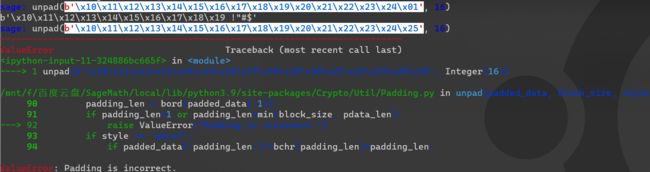
首先他说CTR模式下的AES是流密码,应该有MAC(消息验证码),显然题目中没有提供;其次关键还是在这个pad上,题目采用的是pkcs#7,然后说什么流密码不需要填充啊,填充会让流密码变得不安全啊,因为unpad(ct, 16)这句话,如下图所示,格式错误的在unpad时会报错
所以解密这一步就相当于一个oracle告诉我们猜测的明文pad之后是正确的还是错误的
差不多知道要异或来爆破,但师傅的WP看不懂,主要是encrypted_data ^ wanted_plaintext ^ known_plaintext,只能直接看exp了
发现密码的题目也可以先打本地r = process(["python", "./server.py"]),exp也看不懂
看另外一位师傅的
艹,看不懂啊,最近脑子不行啊,看了好几天,理解不了
padding oracle attack了解一下
Crypto-babyrand(recuring)
from random import randrange
from Crypto.Util.number import getPrime, long_to_bytes
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from hashlib import sha256
from os import urandom
flag = open("flag.txt", "rb").read()
def und():
p = getPrime(512)
x = randrange(p)
a = p ^ x ^ randrange(2**200)
b = p ^ x ^ randrange(2**200)
return p, a, b, x
p,a,b,x = und()
iv = urandom(16)
key = sha256(long_to_bytes(a) + long_to_bytes(b)).digest()[:16]
cipher = AES.new(key, AES.MODE_CBC, iv)
print(f"c1 = {
x}")
print(f"c2 = {
(x*a + b) % p}")
print(f"p = {
p}")
print(f"iv = '{
iv.hex()}'")
print(f"ct = '{
cipher.encrypt(pad(flag, 16)).hex()}'")
已知,注意这里是异或,不然后面不对
a = p ^ x ^ r1
b = p ^ x ^ r2
c2 = ax + b
思路比较简单,最后肯定是要算出a和b的
这里知道a和b的高312位,然后也知道关于a和b的一个二元一次方程,可以试试看之前遇到的Copper解二元方程
竟然不行?
没有一丁点儿思路,去翻别的师傅的WP,在一位日本师傅的博客上找到
首先思路没错,就是用CopperSmith,CopperSmith yyds,但是那个函数的一个参数设置有问题,所以这次放一下github仓库地址,上面有单变量、双变量、三变量以及两个我不是很清楚为什么会在这儿的:boneh_durfee和approximate_factor的例子
参数设置如下
上面的案例我打印出来看了下
f显然是多项式;
bounds是变量的界限,也就是以2^bits的形式,作者说了这是为了优化格子的,所以不用特别的精确;
m确定要使用的f和N的高次幂,我的理解是这个多项式中最大值大约是模数的多少倍,但感觉有点不对;
d确定要使用多少个可变移位。所以这里起码d=2吧
但关于m和d,有一些和案例代码里的对不上,有清楚的师傅能不能ddw
这里之所以第一次没有出来,就是因为roots = small_roots(f, (2^200, 2^200), m=3)[0],正确的应该至少是roots = small_roots(f, (2^200, 2^200), m=1, d=2)[0]。而且m=1, d=2是最快的,几乎一下就出来了,日本师傅的m=3, d=4要过一会,应该也是一个不要求特别严格的值吧
完整的exp
#!/usr/bin/env sage
# -*- coding: utf-8 -*-
from Crypto.Util.number import long_to_bytes
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
from hashlib import sha256
load('coppersmith.sage')
c1 = 5365904711205493895182988721055598679508066289977091231731349423996531384326997250984304389796311073201846992254794801346573036775490182780952712232258774
c2 = 2351499357088933835557969576916974229915931074692169825269157710226395480997304497294813272746195475744137017453323338362896396977337638862808560417575150
p = 12118911800929768381158064532151564397584328623097191996086479213117076586014730135201334840794700976422626122702191630484231703678287738839516304757792517
iv = 'eacdfb3c2cd33a8ce71dbd9a11be89ad'
ct = 'ed36d8614dd35af75251496eef0bb76582dfb83cde59715df41150054be51ac15aaee8eb540a7dbbe58a6fae8287bd9e69043a4800a1e36055d415fd3f41735d3673b3dd5fbdd21941c48ac24ef9b1e288a8848c94e85cd1bda569d2a87c8f33bc790d9aaf97eed583d35a84cc75655cba591d3da9fa3c6e681a2727f2786ffccab3866006cda27d355d8d0665a88a24815b0133a2ff2c8541bc636ac2cc97e03b6189227d3b5469f736ce7373789809de794f987cfe437be56dbb32444055e23023ccd900934ed853ceb3cbac58775a3b7b1c9f3c5a0a32f273ae30ab8a8a9bf24585c39041c262820343eef64735636450dd8628f8a830e109ae3b2b05bef150c98a417b6632ca00c96ee544853955dc948d28dfff28071c5182656fa2ae56614207b9cd96b40cbe28e20bac396577272d341b86ff242daa904e67f226180a02cd2197f8dafda1dd325437e36e457802cefb692bcf0fe9a38addf1d493bd2d40bb972ceff8337fa81a7b9a29ebc6959617a6370b97b90ef8df90e0ea780a0aaea3affa6d7be74118328ca8e3eb060a5afce6f07487ad841382ee82018ba3f452b7f1a0968606739380572364fdfb3a8dac1ca8f856b4aaafbe9c45ad1f81c30f41606e8228ca59482c191af4ecb4f426863dbdbaf76e97a7f5867647e77837dc1b3c843e1a182cf9463f2215afae0d84f975da68d508ca05117de5f5f21a3d818e45cb7612ab052a36edbd7a2386e26777f597c524be57aad5ad254f8b6caa1cc8182d84e8d5a36ea9c5528f4152edb7ce4b5e58529787862a1e9736b2ab135b914835a72fced8485f736a0d7f18bf3d923c66b4c0acede868a3b3970b322675c85dbaf92b985d47bee0ffc18a7a2827dcf449d304d11fb9265d6367e55891f006ab3313a3df6da8c46f6f736b91f31c9c90b782af9a3a527c25f608a0e2ed62d019839587b647b05697c83f3ffafc10d545c8dfc7516e284ab572cd8216b7dcda698eb979f1cd23ba757bc865b51adb337b61bbb682a52fad42741f559a77d863b2ef8af02a8f7776819b02c9b10123c999f626bb563372e9ff141dbc4ac619c52f5a0e245f873b6cadc324e2ed62c6f1858beb8988cfdeb1fa1b223cd1b2ae295c032aa58b46d12c6ace4515561bfb8276ea4b6536aec2b42cfbb64eb30f39d3e79d220da29cd46bd1c8cca85f6c11a8c1b2c265099d51d10651444eea0bbbb556a8de4bf0df8cf9904f4dc7f7840f82a7b4101b7ff499d6f619555c906ce7381c7fe4f165330d76cda4e36ff421a402b1b8bcfcbbc5c80c71ccc9814996723ba4f30f52537bf99547af16bf51bcc6795f7f2cbbf67b0cd0d8d432ff77d17758af8e6309915f152cab18c56495a0b82bdbeb96386a44bb761ee3da3c262d6eb69ee03cc5acbbac45dda3b75a863508bbab3aac1ec8371c1b62753d9a1931c2e8285295902edec528384264c4ccc2d0f9073eae44b81355b82df39f142d3fc5df63e668ea9c6375bea7ee9685830ae39a64ad30af300b4e56fe10b8cd0b0e03488828af68e6fa03f05bc8c38d12c9025e35767f22d67668d081e9827dbe2cfa6ad29d7d7e5bc88135fad55550406226c0c71f16dc901211475e35b8ad97827ee1d0dc3c015b326f884dd3dd8792864a093f73b68169f206606225c85c28af07cd27e35d6b738307629ef71160ac7717f42f0ad26a5f0ddb0aa8940fc72fd054efffe96bb2b5d3d2c68939b256650f9c3db146b69c0a5749b130424a069a2d75b0df890b86c00af1704dbb3f891dea94c152406c1fa636fce8e96db8e4db3f1f4ba2634fd9344664b788b4289acadb0bc543b65018572503d34227ab3ffbce86247cb740dca70c73c85ac29aa646b760314acd0838f0048728cedec961711c2c7f339ea816411cb87ffbc13a7a3e533505df4ac45357b7e002979496343647e33f6d5becfc3c02e357985708f817ea39b9db2cee18af34fe0f93662120e5c496bce6d39f9fc46ef6817f4183227391d73f815cfdbc3a1c58b554b4407a7dfada42945dff9d5f500b8ba588f20f6db575754bada30049a234ea503147cbaf4de8c72f451bd1c47a51d87f9bebf9e738a631863e01ffe7f32e2b620a17ec373acab84eaa0f02a7656a2d39a405c43e770b46c990230b921d9a1e6c38b45ed14011216a41880149eb2392ed7c8e88568f0bcf0e406f91b9ef98adb59bfc45504b6766074058005c059d1422cf7c343fdc88195977e106b42fcf41e95743ced2a670371013ac4cc86e412d7ee9692e0beb540198ab2661fbeebb38be431811f4ab129eb406fa4d6ab2904848941798ab042b0a05622099cf8244045dc4e0006ed30ada599e2f32cc2e474ed836176e7f5e26488295179b67aca112246d63c7a17a86a087087f39c0abce7fbeed200be9daa6cf638685c3feeb5ec265a3f8fd8ae5ad1f86fc08750b636860b1b8bdc309c31da8278f28e7e3326791998f2e74b88da31ad1090156b182b2d11a1fff2dc43a238b1b103519124ed8db6407525d9da8e3773e7652e4b11978ec0d7df57832d96970ec790a11883428a585d6650f13f37c90679aead37055351fd7852472a19bc5d9df2841fada9fbefd432ea15c548924e477642a04c93b681e1326469aa8919262517cee53657134d9effc3bf68752f7ebfb87862cf34e585b1baacbe73062764915d5d6db44a386473ea07cc13d42260aae8919720ccae0e80e09decec61c5c741fd255b5e789734d9a7b86a2500c9b50c009f6b4b96d832a9ddc1695efeb21a7de77b61eadaa4406e0ae58facd6d6b5f4b4b736a335046dadab07d23b4c171270f2e3f0c29154c2dcd10085999106301069f292402a0fc3d0ba19677b921bd70e7bbc501e7bec663dee6aaa2f6cf62cfa3ee268d57721dfb71ff95301514d404e38b67c2753aa4ab4e4be9949fa495c1fc61143b4c4563021bacbb051bdf9419cddaf0e0015655a46fb53a4c7452a0f15ae9fa45cd8bdfab768456912f6cba7ad066ca493714db1abd1625c3d6971264143fe4ef2513e4c4b6f229272271edb8998ad0a9c3e0ed41a792c22b75c6a4c87d37f7b0aa600fb903857453ee137d880e09882535e8e51d719f5ca83d0fa01d71b5115c9190ae95eaafed8a272f9abd5e040aad5042bfbf7399a6f7f2f6932e9ce8ddb856663c6177864cdae1a7d116bb258de586e621b399e870f3909acdbbcbe4fa6f9f2fcb605ed250e11f43fc3c8645ed980d94a5d3a14aab60ba5725a363f845566f170eede27a65a0a2a30865c22aa7d5cafe0ea3252645b8086f3a5443bb8c869990446ddb34e73b99d1d6cb8cdc9c69b94d20785ffde8ad38f92319d56e90a4569d235581656f6f2df761fb792833b4e72207e157841bcc99b3860abfb37f76dd77615420988e1702751e11aa5579e9f1987f3519bfb0fcf835d63b825f9128db50c8c1eccc88a64b4df432c72654371154884c54abc2c5b31693de5265c685dc7e0eeb10bcdca698bfb75016b1dfec2ece20ec4951fd338775d239db1663f63b328d6c6a0415f35f23cffae21a9db195118f22083c5fcbd7192cfa611748cb79486ab78b16b0f1b8d5e81410b0213ff6f603dec71909c6b07bf12618551e4f9c8eaf7346c890b4c10c02970011242a9c57933cdff2526985c0009341474f7d18d197558585feca1cb0030afc784906b45bef19d4cc32b0ae289a08a3eadad86e512100dde8a85d8ab9cc5740cd2e58848b56b7f07defeb43d28aaa6e5a7e46a221323a928088743845b6dc669868634117a50759e5f144f35297374f79e6059a159ca0596fb26273a219fcdc9e5c56a2b9efa0fe392cf54b0c'
x = c1
iv = bytes.fromhex(iv)
ct = bytes.fromhex(ct)
bar = (p ^^ x) >> 200 << 200
Fp = Zmod(p)
bar, x, c2 = map(Fp, [bar, x, c2])
PR.<k0, k1> = PolynomialRing(Fp)
f = x * (bar + k0) + bar + k1 - c2
# m = 2
roots = small_roots(f, (2^200, 2^200), m=1, d=2)[0]
k0, k1 = roots
a = bar + k0
b = bar + k1
key = sha256(long_to_bytes(a) + long_to_bytes(b)).digest()[:16]
cipher = AES.new(key, AES.MODE_CBC, iv)
print(unpad(cipher.decrypt(ct), 16))
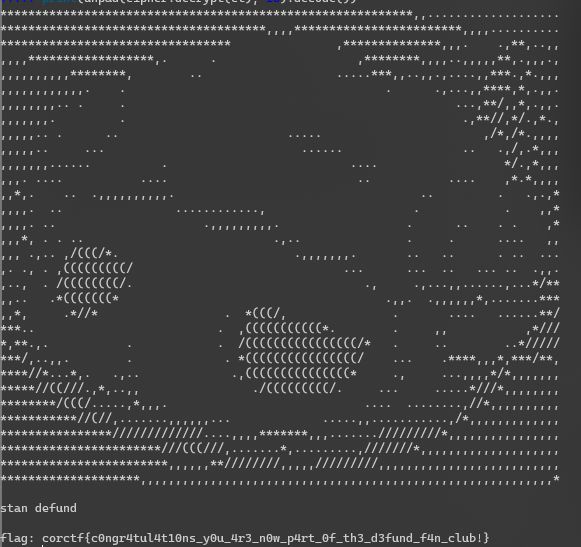
出来的挺奇怪的,但有flag
corctf{c0ngr4tul4t10ns_y0u_4r3_n0w_p4rt_0f_th3_d3fund_f4n_club!}
decode一下,这个头像是啥寓意,评论区有师傅告诉我吗;defund是实现了Copper的github库的主人
我也是defund师傅的小迷弟了
Crypto-LCG_k(unsolved)
对ECDSA没有了解过,做到一半发现求不出来d,搜了发现是椭圆曲线签名,找了la佬和一位师傅的WP去学习了下
LCG?Hey everybody在你头上暴扣
Can you sign my message for me?
nc crypto.be.ax 6002
首先我们来看最后的verify部分
print('now, i want you to sign my message.')
r = int(input('give me r>'))
s = int(input('give me s>'))
if verify(r, s, mymsg):
print("nice. i'll give you the flag.")
print(flag)
else:
print("no, that's wrong.")
想要verify成功,获得flag
def verify(r, s, m):
v1 = H(m)*inverse(s, N) % N
v2 = r*inverse(s, N) % N
V = v1*G + v2*pub
return int(V.x) % N == r
总结一下就是输入r和s,其他的我们都知道,使得该式子成立
m s − 1 x + r s − 1 x d ≡ n r ms^{-1}x+rs^{-1}xd\equiv _nr ms−1x+rs−1xd≡nr
而第一层呢,既是hint,也是我们必须通过的关卡
for _ in range(4):
m = bytes.fromhex(input('give me something to sign, in hex>'))
h = H(m)
if m == mymsg or h in signed_hashes:
print("i won't sign that.")
exit()
signed_hashes.append(h)
r, s = sign(m)
print('r:', str(r))
print('s:', str(s))
看下具体签名的过程
def sign(m):
k = next(gen)
r = int((k*G).x) % N
s = ((H(m) + d*r)*inverse(k, N)) % N
return r, s
r = k x m o d n s = ( m + r d ) ⋅ k − 1 m o d n r=kx\ mod\ n\\ s=(m+rd)\cdot k^{-1}\ mod\ n r=kx mod ns=(m+rd)⋅k−1 mod n
LCG已知模数还可以知道四个状态,可爆
所以应该前面两个状态是用来得到乘数和增量,然后emmmmm似乎求出来LCG也没用,因为不需要预测随机数,而且每次k都可以通过r来算到;所以直接求d吧
我以为的求d
( s k − m ) ⋅ r − 1 ≡ n d (sk-m)\cdot r^{-1}\equiv_n d (sk−m)⋅r−1≡nd
不是 d ∈ [ 0 , n ) d\in [0,\ n) d∈[0, n)吗,左边求出来的不就是d吗,但是操作过后确实不是,暂时不理解;有师傅可以评论区告诉我吗
#!/usr/bin/env sage
# -*- coding: utf-8 -*-
# nc crypto.be.ax 6002
from Crypto.Util.number import bytes_to_long, inverse
from hashlib import sha256
from gmpy2 import *
from fastecdsa.curve import P256
from pwn import *
# context.log_level = 'debug'
sh = remote('crypto.be.ax', 6002)
G = P256.G
N = P256.q
def H(m):
h = sha256()
h.update(m)
return bytes_to_long(h.digest())
def egcd(a, b):
if a == 0:
return b, 0, 1
else:
g, y, x = egcd(b % a, a)
return g, x - (b // a) * y, y
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
raise Exception('modular inverse does not exist')
else:
return x % m
def crack_unknown_increment(states, m, a):
b = (states[1] - states[0] * a) % m
return m, a, b
def crack_unknown_multiplier(states, m):
a = (states[2] - states[1]) * modinv(states[1] - states[0], m) % m
return crack_unknown_increment(states, m, a)
# LCG part
sequence = []
for m in range(4):
inv = invert(G.x, N)
sh.recvuntil(b'give me something to sign, in hex>')
sh.sendline(str(m).encode().hex())
sh.recvuntil(b'r:')
r = int(sh.recvline().decode())
sh.recvuntil(b's:')
s = int(sh.recvline().decode())
k = (int(r) * int(inv)) % N
d = ((int(s) * k - H(str(m).encode())) * int(invert(int(r), N))) % N
print('d =', d)
# d = 111794286037145166785531145837405642417111081891011940999958121590200481323527
# d = 32439466539999346636384702841656953540974828530354787685779441994658571451022
# d = 10926244771926014704519302388552973799549625394927395188718476150973064437377
# d = 114762443346016561170498759027815574796335775581660017547791545655526389133816
师傅说是椭圆曲线数字签名算法,尝试从标准的密码系统上找这里的漏洞
开学了,事情比较多,还是一样的烦心,呵,有空再回来整理了
YauzaCTF
战斗民族的比赛,密码题略少,网站开得了,但是文件下载很慢,但我的网还是在努力下载了,为了我的复现
OSINT主要是看到TIME上的WP,这个方向也挺好玩的,所以想跟着果歪的师傅复现下这两道题,也是看下OSINT手一般会用哪些工具
Crypto-Sharing secrets
import json
from Crypto.Util.number import bytes_to_long, getPrime
from storage import flag
def mul(x):
m = 1
for i in x:
m *= i
return m
if __name__ == '__main__':
flag = bytes_to_long(flag.encode())
count = 25
threshold = 11
psize = 24
primes = list(sorted(getPrime(psize) for _ in range(count)))
pmin = mul(primes[-threshold + 1:])
pmax = mul(primes[:threshold])
assert pmin < flag < pmax
shadows = [flag % x for x in primes]
with open('secrets.json', 'wt') as out_file:
out_file.write(json.dumps({
'shadows': shadows[1:threshold],
'primes': primes[:threshold],
'threshold': threshold
}))
中国剩余定理模数不够,稍微爆破就出来了
#!/usr/bin/env sage
# -*- coding: utf-8 -*-
from Crypto.Util.number import long_to_bytes
shadows = [7832917, 8395798, 4599919, 154544, 3430534, 4694683, 123690, 5911445, 7380167, 10597668]
primes = [8412883, 8889941, 9251479, 9471269, 9503671, 9723401, 10092149, 10389901, 10551241, 10665527, 11099951]
threshold = 11
def mul(x):
m = 1
for i in x:
m *= i
return m
fake_m = crt(shadows, primes[1:])
for j in range(0x10000000):
mi = fake_m + mul(primes[1:]) * j
flag = long_to_bytes(mi)
if b'YauzaCTF' in flag:
print(flag)
break
YauzaCTF{k33p_1t_1n_7h3_sh4d0w5}
Crypto-Knapsack(unsolved)
背包,为什么我没有在遇到WM之前遇到这道题
只给了flag和pubkey,应该和WM的checkin大同小异,flag是加密后得到的结果
flag = [12777998288638, 10593582832873, 7834439533378, 10486500991495, 14714582460036, 7568907598905, 12800035735033, 14724457772647, 11910445040159, 11202963622894, 10291238568620, 15103559399914, 13156142631772, 16988824411176]
pubkey = [2948549611747, 2043155587142, 361533419625, 1001380428657, 2438250374319, 1059738568330, 115120002311, 198226659880, 2343897184958, 2592576935132, 2327834076450, 237536244289, 309228208827, 3327276767693, 462372704541, 2176574227058]
提示:
I decided to keep the secret in my knapsack, so it’s safer.
用WM的脚本跑出来这个
m = [34458, 24238, 49798, 25130, 14046, 11468, 40662, 55034, 11382, 52750, 54828, 9978, 46636, 48758]
然后就没想到了;看这出题量是简单题啊,没道理啊,WM白复现了
OSINT-Stolen Capitalism(unsolved)
English Someone stole bitcoins from the wallet of our Party
bc1qtmyn49urgfu27n30zrghl8499sx42pqrhpm8xt.Find the real name of the thief. The flag matches the specified format.
偷了比特币,找出小偷的真实姓名
稍微去了解了下比特币是什么,随便找了几个视频看了下
比特币是一种数字货币(现在大约有4000多种数字货币,比特币占56%),单位BTC,可以精确到小数点后面很多位;有很多网站和app是用来做比特币交易的
题目中给的这一串bc1qtmyn49urgfu27n30zrghl8499sx42pqrhpm8xt就是某人的bitcoin address,一个人可以拥有多个bitcoin address,由算法生成独一无二的bitcoin address;它的用法有点像支付宝的收款码
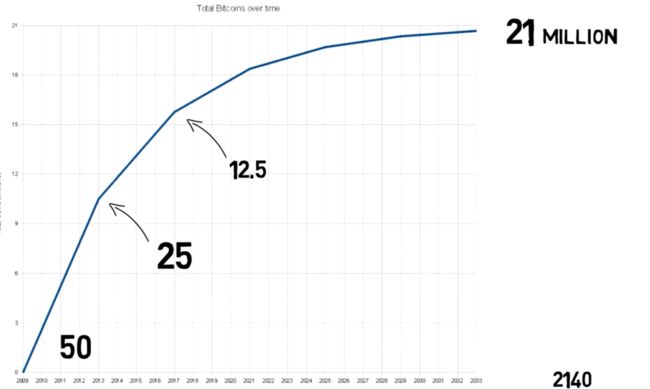
重点来了,比特币的每一笔交易都会记录起来,而记录的手段就是著名的区块链,去中心化是其一个基本的思想,每十分钟都会产生一个新的区块链记录这段时间之内发生的交易;这个链子包含从比特币开始到现在的所有记录。然后有一个很魔性的东西,到底是区块链呢,区块链就是比特币,比特币就是区块链。一个区块链里面50个比特币。
更重点的来了。那么区块链由谁来记录呢?首先肯定是要有人来记录的,来维持整个系统。而做这项工作的人的回报就是比特币。这些人被称为bitcoin miner,也就是挖矿。显然挖比特币的成本就是你的电脑和算力,越多人挖,就越难挖到,也就让比特币的价值变得更高,因为花原来相同的时间挖到比特币的少了
比特币有一个优点,就是不会随着比特币的数量增多而贬值,因为每过四年,一个区块链里的比特币就会减少一半;所以显然,就像黄金一样,比特币是有限的
一些有助于理解的细节
- 每十分钟产生的区块有1M大小,记录约4000条交易信息
- 需要解决几个问题:
- 为何记账:因为有手续续费(由转出方支付),有打包奖励
- 以谁为准:每个包只能由一个人来打,谁能给出工作量证明谁就能打包;而这个就理解成一个要通过计算机枚举才能解出的数学题吧;这也就是上面说的挖矿了,这相当于比特币的扩散手段
- 挖矿的原理:
HASH=SHA256(SHA256(每人都一样的头部信息+每个人各自收集到的账单+时间戳+随机数)),要求HASH值的二进制数前n位是0,因此目前来说只能爆破随机数;为了匹配当前所有矿机的算力,n一般设置为66,当然这可以推导 - 身份认证以及双重支付、篡改等问题,用到密码学、区块链追溯、消息放弃,最长链原则等
开始整活
那么显然我党的钱包地址bc1qtmyn49urgfu27n30zrghl8499sx42pqrhpm8xt有转出,由于区块链的广播公开,网上肯定可以转出的信息
直接搜有点看不懂,可以用页面更好一点的,这里有每一账户所有的交易信息
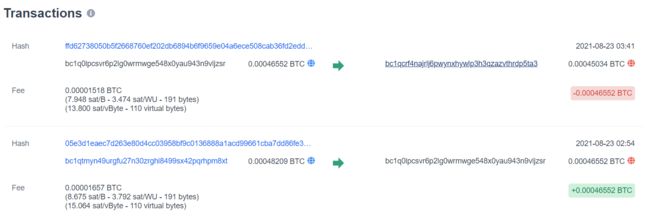
只有两条可以看到18号bc1q27u4g7svl4adwqzp2ds6g6gapph4azpvxj69wm转给bc1qtmyn49urgfu27n30zrghl8499sx42pqrhpm8xt0.00048209BTC,在23号bc1qtmyn49urgfu27n30zrghl8499sx42pqrhpm8xt又向bc1q0lpcsvr6p2lg0wrmwge548x0yau943n9vljzsr转了这笔钱
显然bc1q0lpcsvr6p2lg0wrmwge548x0yau943n9vljzsr就是我们下一步追踪的线索
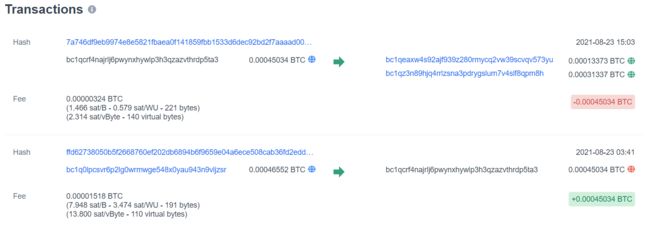
接着又是只有唯一的支出bc1qcrf4najrlj6pwynxhywlp3h3qzazvthrdp5ta3
接着是给两个账户转账:bc1qeaxw4s92ajf939z280rmycq2vw39scvqv573yu和bc1qz3n89hjq4rrlzsna3pdrygslum7v4slf8qpm8h
可以验证,到此为止,这笔钱在到了最后这两个账户后就没有转出记录了
那这四个中,谁是小偷呢?
bc1q0lpcsvr6p2lg0wrmwge548x0yau943n9vljzsr
bc1qcrf4najrlj6pwynxhywlp3h3qzazvthrdp5ta3
bc1qeaxw4s92ajf939z280rmycq2vw39scvqv573yu
bc1qz3n89hjq4rrlzsna3pdrygslum7v4slf8qpm8h
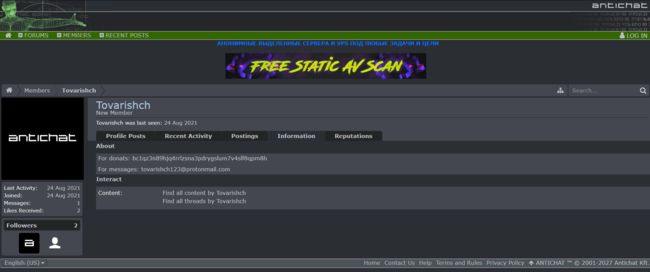
我们用搜索引擎合理搜索,出了关于bitcoin address有关的信息外,在四个中,只有bc1qz3n89hjq4rrlzsna3pdrygslum7v4slf8qpm8h会出来一条特别的信息https://antichat.com/members/413903/
是一个匿名聊天的平台,可以搜到这位id为Tovarishch的一些信息,这里的捐赠就是我们上面找到的比特币地址
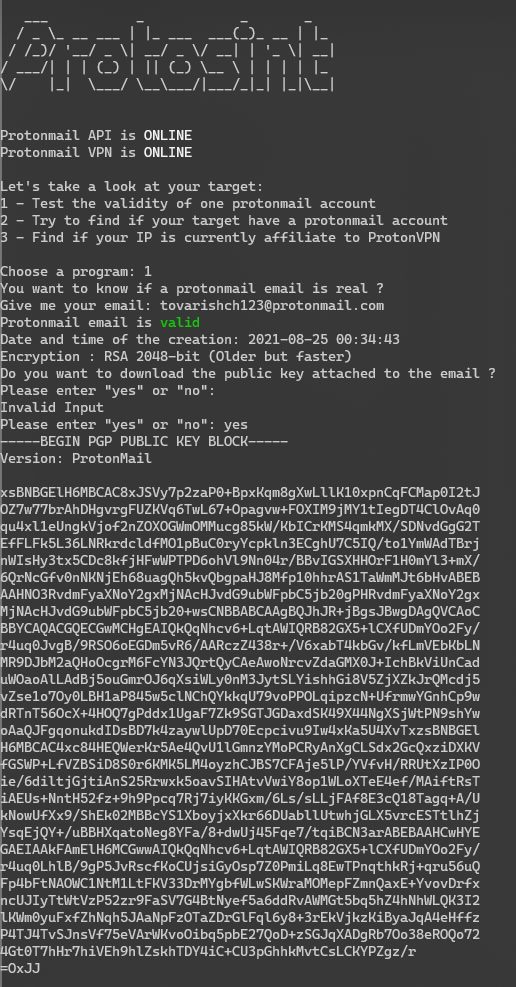
除此之外还能看到一个protonmail邮箱[email protected],师傅说可以用ProtOSINT 去获取更多信息
看到公钥文件是PGP的公钥。Pretty Good Privacy (PGP) 是一种加密系统,用于发送加密电子邮件和加密敏感文件;从创建的日期看也是为了比赛而创建的,方向应该没错
我试过用keyserver搜索
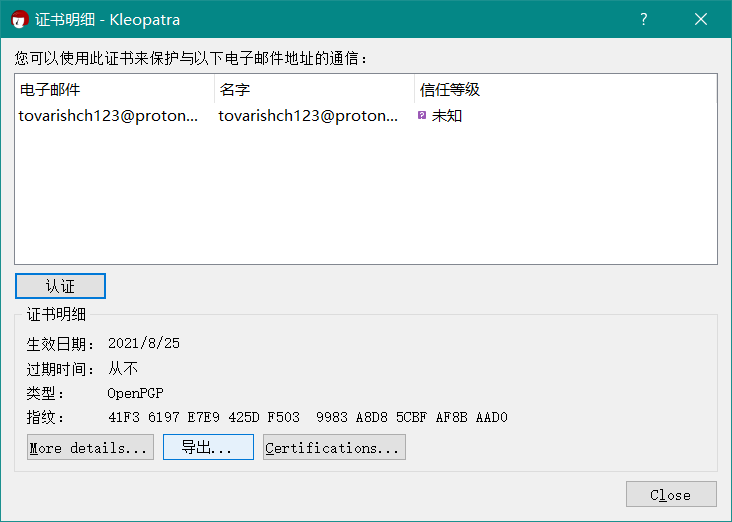
也和用师傅所说的Kleopatra去看了下,反正就是没有的
我尝试直接用搜索引擎去搜索,在StopForumSpam一个阻止机器人垃圾邮件的论坛上,搜到了该邮箱的踪影
同一个ip地址下有这两封邮件
但用户名提交都不对
没事,那个匿名聊天平台还有别的信息,总共有两篇帖子,这个翻译。。
师傅说是Reliable mixers Msg: Recommend a good proven bitcoin mixer Msg (rusky),和比特币混合器有关,反正就是龟孙没跑了
另外一篇是转发YouTube上的视频
这个条评论确实可疑
然后剩下是师傅整理的一些时间节点
感觉前面都挺顺利和确定的,但是从这个视频开始,一切就不确定起来
专业的师傅不会,业余的我更不会了哈哈哈哈,虽然这道题比下一道出的更多
OSINT-Get in touch(recuring)
English: Our best agent is going to send us a message from an enemy country. But instead, he just posted some stupid player on his page! Find his public key immediately and send us the first 42 symbols in an appropriate form so we can be sure it’s him. For example, YAUZActf{Tgj8t6gbK9zlv4Xmivyhttjzvfbbp7nuqkce3uuomF}
tasks.yauzactf.com:30010
提供的是网址,我还以为nc;浏览器打开之后,有几个YouTube的视频
可以看一下网页源码
DOCTYPE html>
<html>
<body style="background-color: red;">
<link rel="stylesheet" href="https://cdn.plyr.io/3.6.8/plyr.css" />
<script src="https://cdn.plyr.io/3.6.8/plyr.polyfilled.js">script>
<div hidden class="plyr__video-embed" id="player1">
<iframe
src="https://www.youtube.com/embed/DMoCM_FgLP8"
allowfullscreen
allowtransparency
allow="autoplay"
>iframe>
div>
<div hidden class="plyr__video-embed" id="player2">
<iframe
src="https://www.youtube.com/embed/Bwf9f498Yqs"
allowfullscreen
allowtransparency
allow="autoplay"
>iframe>
div>
<div hidden class="plyr__video-embed" id="player3">
<iframe
src="https://www.youtube.com/embed/o2mD5hv0eMc"
allowfullscreen
allowtransparency
allow="autoplay"
>iframe>
div>
<script>
function which_playlist_i_want_to_listen() {
var currenthour = new Date().getHours();
switch(currenthour % 3) {
case 0:
var elem = document.getElementById("player1");
elem.removeAttribute("hidden");
break;
case 1:
var elem = document.getElementById("player2");
elem.removeAttribute("hidden");
break;
case 2:
var elem = document.getElementById("player3");
elem.removeAttribute("hidden");
break;
}
}
which_playlist_i_want_to_listen();
script>
body>
html>
挺怪的,战斗民族喜欢看这些?宇航器挺帅的,Our Dream听着挺空灵的,我当bgm了
YCS插件可以对YouTube的评论进行筛选,点save可以下载,可以用脚本去正则匹配你所想要的
但这位师傅上述操作无果,竟然想到在github上搜which_playlist_i_want_to_listen这个源代码里的函数名,而且确实有;注意,不是在搜索引擎里搜,而是在github内搜,学到了
是一模一样的源码https://github.com/znak-kachestva/sovietwave-player/blob/main/index.html
而且可以看出主人的账号是在前不久刚创建的,与比赛的时间吻合,CCCP就是苏联,尝试搜索这位znak-kachestva
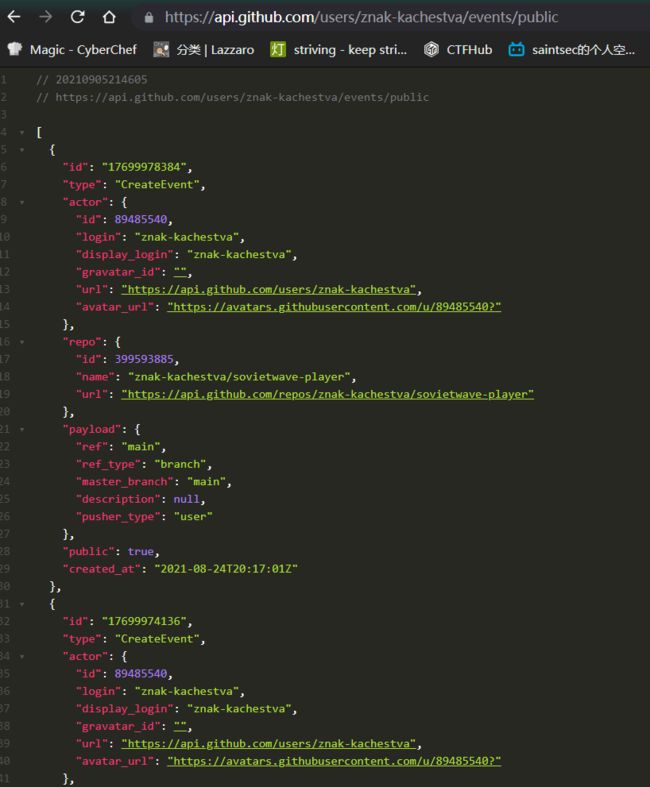
通过将用户名替换该网址的可以搜索该用户在库中的一些操作
https://api.github.com/users/<github-username>/events/public
像这样,师傅说想拿来作为找邮箱的
然后显然这里并没有邮箱,因为github默认设置了隐私
然后这位师傅就很CTFer得想到第一题的邮箱可不可以拿来用
这里师傅演示了怎么用电子邮件发现GitHub帐户,这是他罗列的步奏
我跟着操作了下,最近也在玩github,学点
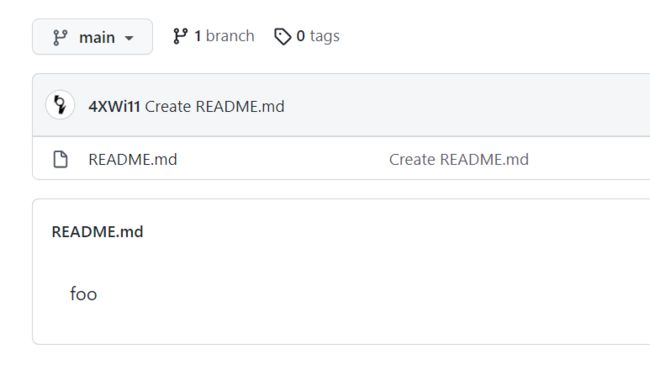
在自己的github上创建一个库,名字随便取,文件随便加,复制这个的链接
然后打开Git Bash,然后在cd到你合适的目录,clone下来刚才创立的远程库,随便加一个文件,我这里把Crypto题的一个脚本复制过去了,然后输入git add *添加文件,依照如下代码设置
git commit -m "bar" --author="foo "
最后输入git push origin main给push过去就好,如果push过程有问题可以参考这篇博客
完成后可以看到,刚才头像的那个人竟然和我在共同编写这个库
在commit hash的.patch里面可以看到,确实是该邮箱与那个github的账号相关联
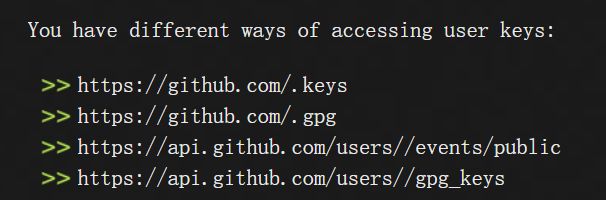
最后说可以从API访问而不是使用电子邮件访问的GitHub SSH、PGP和GPG密钥
是在最后一个这里https://api.github.com/users/znak-kachestva/gpg_keys找到的
还有一个假的
也可以直接访问这个网址直接获得干净的公钥https://github.com/znak-kachestva.gpg
最后根据题目意思,提交公钥的前42位就好了
YauzaCTF{xo0EYSVYlQEEANaoJXa6DarxrVc8OWpexZxAq0z8a7}
确实,正如师傅所有,OSINT方向对学习github的使用也很有帮助