机器学习/深度学习实战——kaggle房价预测比赛实战(机器学习回归算法)
文章目录
-
- 3. 构建模型
-
- 3.1 使用lazyPredict寻找最优拟合算法
- 3.2 超参数调整
- 3.3 Ridge Regression
- 3.4 Lasso Regression
- 3.5 Gradient Boosting Regressor
- 3.6 XGBRegressor
- 3.7 LGBMRegressor
- 3.8 StackingRegressor
- 3. 9 保存模型
- 4. 输出预测结果
相关BLOG:
- 第1个blog:数据分析
- 第2个blog:数据预处理
- 第3个blog:应用机器学习回归分析算法进行建模和预测
- 第4个blog:应用pytorch设计深度学习模型
相关数据及比赛地址:
kaggle 比赛:House Prices - Advanced Regression Techniques
数据下载地址:百度网盘 提取码: w2t6
3. 构建模型
3.1 使用lazyPredict寻找最优拟合算法
lazyregressor输出结果说明:
-
- Adjusted R-Squared:校正决定系数
R a d j u s t e d 2 = 1 − ( 1 − R 2 ) ( n − 1 ) n − p − 1 R^2_{adjusted} = 1 - \frac{(1-R^2)(n-1)}{n-p-1} Radjusted2=1−n−p−1(1−R2)(n−1)
其中n为样本数量,p为特征数量。Adjusted R-Square系取值范围为负无穷到1,大多数是0~1,值越大越好。
- Adjusted R-Squared:校正决定系数
-
- R-Square(决定系数)
R 2 = 1 − ∑ ( Y a c t u a l − Y p r e d i c t ) 2 ∑ ( Y a c t u a l − Y m e a n ) 2 R^2 = 1 - \frac{\sum(Y_{actual} - Y_{predict})^2}{\sum({Y_{actual} - Y_{mean})^2}{}} R2=1−∑(Yactual−Ymean)2∑(Yactual−Ypredict)2
此处的R为相关系数,相关系数的平方即R-Square。R-Square表示该模型能够拟合的“变化程度”,占真实数据的“变化程度”的比例。一般认为,R-Square越大越好
- R-Square(决定系数)
- 3)RMSE:均方根误差
R M S E ( X , h ) = 1 m ∑ i = 1 m ( h ( x i ) − y i ) 2 RMSE(X,h) = \sqrt{\frac{1}{m}\sum_{i=1}^{m}{(h(x_i) - y_i)^2}} RMSE(X,h)=m1i=1∑m(h(xi)−yi)2
参考文章:
(机器学习)如何评价回归模型?——Adjusted R-Square(校正决定系数)
Lazy Predict:一行代码完成所有sklearn模型的拟合和评估
x_train1,x_test1,y_train1,y_test1 = train_test_split(X_train,y_train,test_size=0.25)
reg = LazyRegressor(verbose=0,ignore_warnings=True,custom_metric=None)
train,test = reg.fit(x_train1,x_test1,y_train1,y_test1)
test
| Adjusted R-Squared | R-Squared | RMSE | Time Taken | |
|---|---|---|---|---|
| Model | ||||
| HuberRegressor | 0.62 | 0.90 | 0.11 | 0.10 |
| ElasticNetCV | 0.58 | 0.89 | 0.12 | 0.47 |
| LassoCV | 0.58 | 0.89 | 0.12 | 0.49 |
| GradientBoostingRegressor | 0.55 | 0.88 | 0.12 | 0.47 |
| BayesianRidge | 0.55 | 0.88 | 0.12 | 0.14 |
| PoissonRegressor | 0.54 | 0.88 | 0.13 | 0.04 |
| GeneralizedLinearRegressor | 0.54 | 0.88 | 0.13 | 0.02 |
| TweedieRegressor | 0.54 | 0.88 | 0.13 | 0.02 |
| GammaRegressor | 0.54 | 0.88 | 0.13 | 0.02 |
| HistGradientBoostingRegressor | 0.53 | 0.88 | 0.13 | 0.82 |
| LGBMRegressor | 0.52 | 0.88 | 0.13 | 0.08 |
| RidgeCV | 0.52 | 0.88 | 0.13 | 0.07 |
| Ridge | 0.51 | 0.87 | 0.13 | 0.02 |
| LassoLarsCV | 0.49 | 0.87 | 0.13 | 0.20 |
| LinearSVR | 0.47 | 0.86 | 0.13 | 0.45 |
| ExtraTreesRegressor | 0.47 | 0.86 | 0.14 | 1.46 |
| RandomForestRegressor | 0.45 | 0.86 | 0.14 | 1.32 |
| OrthogonalMatchingPursuit | 0.41 | 0.85 | 0.14 | 0.02 |
| XGBRegressor | 0.40 | 0.84 | 0.14 | 0.19 |
| LassoLarsIC | 0.39 | 0.84 | 0.14 | 0.07 |
| NuSVR | 0.36 | 0.83 | 0.15 | 0.72 |
| OrthogonalMatchingPursuitCV | 0.32 | 0.82 | 0.15 | 0.05 |
| SVR | 0.31 | 0.82 | 0.15 | 0.20 |
| BaggingRegressor | 0.30 | 0.82 | 0.15 | 0.15 |
| PassiveAggressiveRegressor | 0.27 | 0.81 | 0.16 | 0.03 |
| LarsCV | 0.26 | 0.81 | 0.16 | 0.56 |
| AdaBoostRegressor | 0.21 | 0.80 | 0.16 | 0.27 |
| SGDRegressor | 0.05 | 0.75 | 0.18 | 0.05 |
| KNeighborsRegressor | -0.04 | 0.73 | 0.19 | 0.18 |
| ExtraTreeRegressor | -0.29 | 0.67 | 0.21 | 0.04 |
| DecisionTreeRegressor | -0.41 | 0.64 | 0.22 | 0.05 |
| Lasso | -2.90 | -0.01 | 0.37 | 0.06 |
| ElasticNet | -2.90 | -0.01 | 0.37 | 0.04 |
| DummyRegressor | -2.90 | -0.01 | 0.37 | 0.02 |
| LassoLars | -2.90 | -0.01 | 0.37 | 0.02 |
| MLPRegressor | -35.49 | -8.42 | 1.12 | 1.69 |
| GaussianProcessRegressor | -4159.81 | -1073.50 | 11.96 | 0.25 |
| KernelRidge | -4217.15 | -1088.30 | 12.04 | 0.04 |
| LinearRegression | -32618686027315109953536.00 | -8423506831229725966336.00 | 33488872000.27 | 0.11 |
| TransformedTargetRegressor | -32618686027315109953536.00 | -8423506831229725966336.00 | 33488872000.27 | 0.02 |
| RANSACRegressor | -95835413005320964800512.00 | -24748705556319151587328.00 | 57402432649.95 | 3.64 |
| Lars | -2708399284498913352297337244581162553831478046... | -6994217932497193705011541606563145240878470974... | 30515720854749324937003008.00 | 0.12 |
选择精度高而用时少的算法(嗯?我是那种缺时间的人么,所以先随便选择几种算法做测试):
- HuberRegressor
- ElasticNetCV
- LassoCV
- GradientBoostingRegressor
- BayesianRidge
3.2 超参数调整
K-折交叉验证
RANDOM_SEED = 1 # 给个种子,方便复现
# 10-fold CV
kfolds = KFold(n_splits=10,shuffle=True,random_state=RANDOM_SEED)
def tune(objective):
study = optuna.create_study(direction='maximize')
study.optimize(objective,n_trials=100)
params = study.best_params
best_score = study.best_value
print(f"Best score: {
best_score} \nOptimized parameters: {
params}")
return params
3.3 Ridge Regression
def ridge_objective(trial):
_alpha = trial.suggest_float("alpha",0.1,20)
ridge = Ridge(alpha=_alpha,random_state=RANDOM_SEED)
score = cross_val_score(
ridge,X_train,y_train, cv=kfolds, scoring="neg_root_mean_squared_error"
).mean()
return score
ridge_params = {
'alpha': 19.997759851201025}
ridge = Ridge(**ridge_params, random_state=RANDOM_SEED)
ridge.fit(X_train,y_train)
Ridge(alpha=19.997759851201025, random_state=1)
3.4 Lasso Regression
def lasso_objective(trial):
_alpha = trial.suggest_float("alpha", 0.0001, 1)
lasso = Lasso(alpha=_alpha, random_state=RANDOM_SEED)
score = cross_val_score(
lasso,X_train,y_train, cv=kfolds, scoring="neg_root_mean_squared_error"
).mean()
return score
# Best score: -0.13319435700230317
lasso_params = {
'alpha': 0.0006224224345371836}
lasso = Lasso(**lasso_params, random_state=RANDOM_SEED)
lasso.fit(X_train,y_train)
Lasso(alpha=0.0006224224345371836, random_state=1)
3.5 Gradient Boosting Regressor
def gbr_objective(trial):
_n_estimators = trial.suggest_int("n_estimators", 50, 2000)
_learning_rate = trial.suggest_float("learning_rate", 0.01, 1)
_max_depth = trial.suggest_int("max_depth", 1, 20)
_min_samp_split = trial.suggest_int("min_samples_split", 2, 20)
_min_samples_leaf = trial.suggest_int("min_samples_leaf", 2, 20)
_max_features = trial.suggest_int("max_features", 10, 50)
gbr = GradientBoostingRegressor(
n_estimators=_n_estimators,
learning_rate=_learning_rate,
max_depth=_max_depth,
max_features=_max_features,
min_samples_leaf=_min_samples_leaf,
min_samples_split=_min_samp_split,
random_state=RANDOM_SEED,
)
score = cross_val_score(
gbr, X_train,y_train, cv=kfolds, scoring="neg_root_mean_squared_error"
).mean()
return score
gbr_params = {
'n_estimators': 1831, 'learning_rate': 0.01325036780847096, 'max_depth': 3, 'min_samples_split': 17, 'min_samples_leaf': 2, 'max_features': 29}
gbr = GradientBoostingRegressor(random_state=RANDOM_SEED, **gbr_params)
gbr.fit(X_train,y_train)
GradientBoostingRegressor(learning_rate=0.01325036780847096, max_features=29,
min_samples_leaf=2, min_samples_split=17,
n_estimators=1831, random_state=1)
3.6 XGBRegressor
def xgb_objective(trial):
_n_estimators = trial.suggest_int("n_estimators", 50, 2000)
_max_depth = trial.suggest_int("max_depth", 1, 20)
_learning_rate = trial.suggest_float("learning_rate", 0.01, 1)
_gamma = trial.suggest_float("gamma", 0.01, 1)
_min_child_weight = trial.suggest_float("min_child_weight", 0.1, 10)
_subsample = trial.suggest_float('subsample', 0.01, 1)
_reg_alpha = trial.suggest_float('reg_alpha', 0.01, 10)
_reg_lambda = trial.suggest_float('reg_lambda', 0.01, 10)
xgbr = xgb.XGBRegressor(
n_estimators=_n_estimators,
max_depth=_max_depth,
learning_rate=_learning_rate,
gamma=_gamma,
min_child_weight=_min_child_weight,
subsample=_subsample,
reg_alpha=_reg_alpha,
reg_lambda=_reg_lambda,
random_state=RANDOM_SEED,
)
score = cross_val_score(
xgbr, X_train,y_train, cv=kfolds, scoring="neg_root_mean_squared_error"
).mean()
return score
xgb_params = {
'n_estimators': 847, 'max_depth': 7, 'learning_rate': 0.07412279963454066, 'gamma': 0.01048697764796929, 'min_child_weight': 5.861571837417184, 'subsample': 0.7719639391828977, 'reg_alpha': 2.231609305115769, 'reg_lambda': 3.428674606766844}
xgbr = xgb.XGBRegressor(random_state=RANDOM_SEED, **xgb_params)
xgbr.fit(X_train,y_train)
XGBRegressor(base_score=0.5, booster='gbtree', colsample_bylevel=1,
colsample_bynode=1, colsample_bytree=1, gamma=0.01048697764796929,
gpu_id=-1, importance_type='gain', interaction_constraints='',
learning_rate=0.07412279963454066, max_delta_step=0, max_depth=7,
min_child_weight=5.861571837417184, missing=nan,
monotone_constraints='()', n_estimators=847, n_jobs=0,
num_parallel_tree=1, random_state=1, reg_alpha=2.231609305115769,
reg_lambda=3.428674606766844, scale_pos_weight=1,
subsample=0.7719639391828977, tree_method='exact',
validate_parameters=1, verbosity=None)
3.7 LGBMRegressor
def lgb_objective(trial):
_num_leaves = trial.suggest_int("num_leaves", 50, 100)
_max_depth = trial.suggest_int("max_depth", 1, 20)
_learning_rate = trial.suggest_float("learning_rate", 0.01, 1)
_n_estimators = trial.suggest_int("n_estimators", 50, 2000)
_min_child_weight = trial.suggest_float("min_child_weight", 0.1, 10)
_reg_alpha = trial.suggest_float('reg_alpha', 0.01, 10)
_reg_lambda = trial.suggest_float('reg_lambda', 0.01, 10)
_subsample = trial.suggest_float('subsample', 0.01, 1)
lgbr = lgb.LGBMRegressor(objective='regression',
num_leaves=_num_leaves,
max_depth=_max_depth,
learning_rate=_learning_rate,
n_estimators=_n_estimators,
min_child_weight=_min_child_weight,
subsample=_subsample,
reg_alpha=_reg_alpha,
reg_lambda=_reg_lambda,
random_state=RANDOM_SEED,
)
score = cross_val_score(
lgbr, X_train,y_train, cv=kfolds, scoring="neg_root_mean_squared_error"
).mean()
return score
# Best score: -0.12497294451988177
# lgb_params = tune(lgb_objective)
lgb_params = {
'num_leaves': 81, 'max_depth': 2, 'learning_rate': 0.05943111506493225, 'n_estimators': 1668, 'min_child_weight': 4.6721695700874015, 'reg_alpha': 0.33400189583009254, 'reg_lambda': 1.4457484337302167, 'subsample': 0.42380175866399206}
lgbr = lgb.LGBMRegressor(objective='regression', random_state=RANDOM_SEED, **lgb_params)
lgbr.fit(X_train,y_train)
LGBMRegressor(learning_rate=0.05943111506493225, max_depth=2,
min_child_weight=4.6721695700874015, n_estimators=1668,
num_leaves=81, objective='regression', random_state=1,
reg_alpha=0.33400189583009254, reg_lambda=1.4457484337302167,
subsample=0.42380175866399206)
3.8 StackingRegressor
# stack models
stack = StackingRegressor(
estimators=[
('ridge', ridge),
('lasso', lasso),
('gradientboostingregressor', gbr),
('xgb', xgbr),
('lgb', lgbr),
# ('svr', svr), # Not using this for now as its score is significantly worse than the others
],
cv=kfolds)
stack.fit(X_train,y_train)
StackingRegressor(cv=KFold(n_splits=10, random_state=1, shuffle=True),
estimators=[('ridge',
Ridge(alpha=19.997759851201025, random_state=1)),
('lasso',
Lasso(alpha=0.0006224224345371836,
random_state=1)),
('gradientboostingregressor',
GradientBoostingRegressor(learning_rate=0.01325036780847096,
max_features=29,
min_samples_leaf=2,
min_samples_split=17,
n_estima...
subsample=0.7719639391828977,
tree_method='exact',
validate_parameters=1,
verbosity=None)),
('lgb',
LGBMRegressor(learning_rate=0.05943111506493225,
max_depth=2,
min_child_weight=4.6721695700874015,
n_estimators=1668, num_leaves=81,
objective='regression',
random_state=1,
reg_alpha=0.33400189583009254,
reg_lambda=1.4457484337302167,
subsample=0.42380175866399206))])
3. 9 保存模型
def cv_rmse(model):
rmse = -cross_val_score(model, X_train,y_train,
scoring="neg_root_mean_squared_error",
cv=kfolds)
return (rmse)
def compare_models():
models = {
'Ridge': ridge,
'Lasso': lasso,
'Gradient Boosting': gbr,
'XGBoost': xgbr,
'LightGBM': lgbr,
'Stacking': stack,
# 'SVR': svr, # TODO: Investigate why SVR got such a bad result
}
scores = pd.DataFrame(columns=['score', 'model'])
for name, model in models.items():
score = cv_rmse(model)
print("{:s} score: {:.4f} ({:.4f})\n".format(name, score.mean(), score.std()))
df = pd.Series(score, name='score').to_frame()
df['model'] = name
scores = scores.append(df)
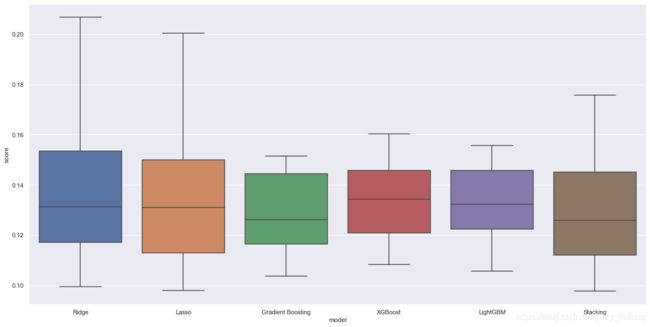
plt.figure(figsize=(20,10))
sns.boxplot(data = scores, x = 'model', y = 'score')
plt.show()
compare_models()
Ridge score: 0.1362 (0.0303)
Lasso score: 0.1341 (0.0294)
Gradient Boosting score: 0.1278 (0.0172)
XGBoost score: 0.1330 (0.0161)
LightGBM score: 0.1330 (0.0166)
Stacking score: 0.1289 (0.0230)
4. 输出预测结果
这里有一个submission.csv,是在下载数据包里面给定的sample_submission.csv,主要是获取其格式。
print('Predict submission')
submission = pd.read_csv("submission.csv")
submission.iloc[:,1] = np.expm1(stack.predict(X_test))
submission.to_csv('submission_2.csv', index=False)
我没有进行进一步的超参数微调,直接将一遍处理之后的结果提交到了比赛官网,排名从之前的20000上升到了大概4000的样子,说明对数据进行预处理之后是可以极大地提高建模的效果。同时使用传统的机器学习算法通过stacking的方法也是可以提高学习的