数据结构之图论算法（一）图的存储结构及其构建算法
数据结构之图论算法（一）图的存储结构
总：图 = 顶点 + 边
1、邻接矩阵存储结构（数组表示法）（Adjacency Matrix）
- 边——二位数组中每个元素及其值
#define INFINITY INT_MAX //最大值，表示无穷大
#define MAX_VERTEX_NUM 20 //最大顶点个数，英文vertex的意思为：顶点
typedef int VRType; //VRtype是顶点关系类型（Vertex Relation type）。
typedef struct ArcCell{
//arc：弧。二维数组中每个元素的数据类型为ArcCell
VRType adj; //表示是否相邻；
//对于带权图，则为权值类型；
//对无权图，用1或0；
InfoType *info; //该弧相关信息的指针；
}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
- 顶点——顶点表（一维数组）
- 图——二维数组整体
（因为数组表示法的特殊性，所以图与顶点一起构建，定义如下：）
typedef enum{
DG, DN, AG, AN}Graphkind; //{有向图，有向网，无向图，无向网}
typedef struct{
VertexType vexs[MAX_VERTEX_NUM]; //顶点向量,即顶点表
AdjMatrix arcs; //arc+s：由多个弧组成的邻接矩阵（二位数组），各元素的类型为ArcCell
int vexnum, arcnum; //图的当前顶点数和边数
Graphkind kind; //图的种类标志
}MGraph;
设图为：A = （V，E），则
注意：A.arcs[ i ][ i ] = 0
上面是无向图的情况。其邻接矩阵是对称的。而有向图的邻接矩阵中，将列看为“出”，行看为“入”， 所以列上的顶点出，行上的顶点入，满足的才是1。因此，有向图不一定对称。
有向网络的邻接矩阵也是同理：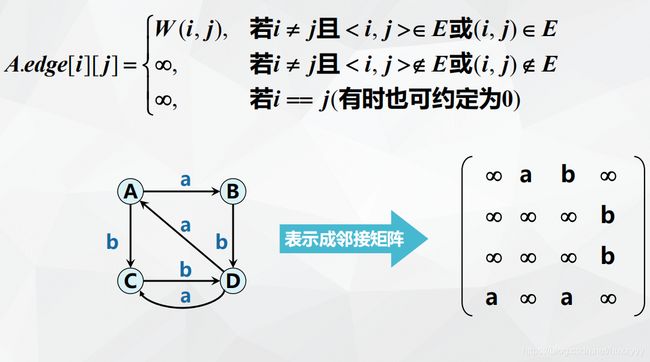
图的创建的算法表示：
//构造无向图的算法：
Status CreateUDN(MGraph &G){
//采用数组（邻接矩阵）表示法，构造无向网G
//相关函数申明
int LocateVex(MGraph, VertexType);
void Input(InfoType *);
int i,j,k, IncInfo; //用IncInfo来标志是否有弧的相关信息
scanf("%d %d %d",&G.vexnum,&G.arcnum, &IncInfo);//分别记录顶点数、弧数、是否存在弧信息（如果IncInfo为0则各弧不含其他信息）
for(i = 0; i < G.vexnum; i++) scanf(&G.vexs[i]);//构造顶点向量
//初始化邻接矩阵
for(i = 0; i < G.vexnum; i++)
for(j = 0; j < G.vexnum; j++){
G.arcs[i][j].adj = INFINITY;
G.arcs[i][j].info = NULL;
}
//构造邻接矩阵
VertexType v1, v2;
VRType w;
for(k = 0; k < G.arcnum;k++){
scanf(&v1, &v2, &w); //输入一条边依附的两个顶点及其权值
i = LocateVex(G, v1); j = LocateVex(G, v2);//确定v1, v2在G中的位置
G.arcs[i][j].adj = w; //弧的权值
if(IncInfo) Input(G.arcs[i][j].info); //若弧含有相关信息，则输入
G.arcs[j][i] = G.arcs[i][j]; //置的对称弧
}
return OK;
}
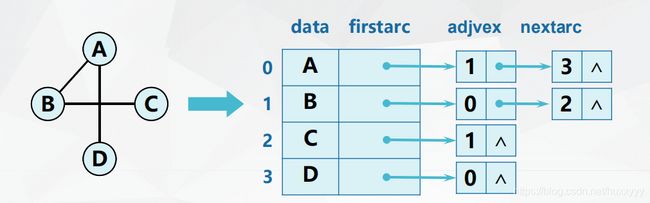
2、邻接表存储结构（Adjacency List）
- 顶点结点——类似于静态链表
| 顶点域 | 边头结点指针 |
|---|---|
| data | firstarc |
#define MAX_VERTEX_NUM 20
typedef struct VNode{
VertexType data; //顶点信息
ArcNode *firstarc; //指向第一条依附该顶点的边的指针，所以指针类型应为边的类型
}VNode,AdjList[MAX_VERTEX_NUM]; //AdjList表示邻接表类型
- 弧结点——类似于动态链表
| 邻接点域 | 权值 | 指针域 |
|---|---|---|
| adjvex | info | nextarc |
typedef struct ArcNode{
int adjvex; //表示该边指向的顶点的位置
InfoType *info; //和边相关的信息
struct ArcNode *nextarc; //指向下一条边
}ArcNode;
- 图——顶点构成的静态链表+图的当前顶点数和弧数
typedef struct{
AdjList vertices; //vertices是vertex的复数
int vexnum, arcnum; //图的当前顶点数和边数
}ALGraph;
算法思想：（采用邻接表创建无向网）
- 输入总顶点数和总边数；
- 建立顶点表：
依次输入点的信存入顶点表中，使每个表头结点的指针域初始化为NULL - 建立邻接表：
依次输入每条边依附的两个顶点，确定两个顶点的序号i和j，建立边结点；
将此边结点分别插入vi和vj对应的两个边链表的头部
Status CreateUDG(ALGraph &G){
//采用邻接表创建无向图G
int LocateVex(ALGraph, VertexType);
int i, k, j;
VertexType v1, v2;
ArcNode *p1, *p2;
scanf("%d %d", &G.vexnum, &G.arcnum); //输入总顶点数、总边数
for(i = 0; i < G.vexnum; i++){
//输入各点，构造表头结点（类似于邻接矩阵的顶点表的建立）
scanf("%d", G.vertices[i].data);
G.vertices[i].firstarc = NULL;
}
for(k = 0; k < G.arcnum; k++){
//输入各边，构造邻接表（构造边）
scanf(&v1,&v2); //输入边依附的两个顶点
i = LocateVex(G, v1); //确定顶点在图G中的位置
j = LocateVex(G, v2);//以上都和创建邻接矩阵相同。
//无向网，相当于边既是从i指向j又是从j指向i
//1.边从i(v1)指向j(v2)：[v1出发到v2]
p1 = (ArcNode *)malloc(sizeof(ArcNode)); //分配一条边的空间
p1->adjvex = j; //边指向结点j(v2)
p1->nextarc = G.vertices[i].firstarc; //把原来头结点指向的边的地址给新结点；
//如果原头结点的firstarc为NULL，则现在变为NULL；
//如果原头结点的firstarc非空，相当于是在原来的头结点和边结点之间插入新结点。
G.vertices[i].firstarc = p1;//最后将头结点指向新结点
//2.边从j(v2)指向i(v1)：[v2出发到v1]
p2 = (ArcNode *)malloc(sizeof(ArcNode)); //先分配边大小的空间
p2->adjvex = i; //边指向结点i(v1)
p2->nextarc = G.vertices[j].firstarc; //在原来的头节点及其指向的结点之间插入新结点
G.vertices[j].firstarc = p2; //使头结点指向新结点
}
return OK;
}
十字链表存储结构
顶点结点：
| 数据域 | 头链表头指针 | 尾链表头指针 |
|---|---|---|
| data | firstin | firstout |
typedef struct VexNode{
VertexType data;
ArcBox *firstin, *firstout; //分别指向该顶点第一条入弧和出弧
}VexNode;
弧结点：
| 尾域 | 头域 | 头链域 | 尾链域 | 数据域 |
|---|---|---|---|---|
| tailvex | headadvex | hlink | tlink | info |
typedef struct ArcBox{
int tailvex, headvex; //该弧的尾和头顶点的位置
struct ArcBox *hlink, *tlink; //分别为弧头相同和弧尾相同的弧的链域
InfoType *info; //该弧相关信息的指针
}ArcBox;
图：顶点表+有向图的总顶点数和总边数
typedef struct{
VexNode xlist[MAX_VERTEX_NUM]; //表头向量
int vexnum, arcnum; //有向图的当前顶点数和弧数
}OLGraph;
用十字链表构造有向图的算法表示：
Status CreateDG(OLGraph &G){
//采用十字链表存储表示，构造有向G（G.kind = DG）
//函数申明
int LocateVex(OLGraph, VertexType);
void Input(InfoType);
VertexType v1, v2;
ArcBox *p;
int IncInfo, i, j, k;
scanf("%d %d %d", &G.vexnum, &G.arcnum, &IncInfo); //IncInfo为0则各弧不含其他信息
for(i = 0; i < G.vexnum; i++){
//构造顶点表
scanf("%d",&G.xlist[i].data); //输入顶点值
G.xlist[i].firstin = NULL; G.xlist[i].firstout = NULL; //指针初始化
}
for(k = 0; k < G.arcnum; k++){
//输入各弧并构造十字链表
scanf(&v1, &v2); //输入一条弧的起始点和终点
i = LocateVex(G, v1);j = LocateVex(G, v2); //确定v1和v2在G中的位置
p = (ArcBox*)malloc(sizeof(ArcBox)); //分配给p一个边
p->tailvex = i;p->headvex = j; //对弧结点赋值，可以一次性赋完
p->hlink = G.xlist[j].firstin;p->tlink = G.xlist[i].firstout;
p->info = NULL;
G.xlist[j].firstin = G.xlist[i].firstout = p; //完成在入弧和出弧立链头之间的插入（类似于邻接表的插入）
if(IncInfo) Input(*p->info); //若弧含有相关信息，则输入
}
return OK;
}
可以说十字链表是邻接表的进阶版
临界多重表存储结构
顶点结点：
| 数据域 | 链表头指针 |
|---|---|
| data | firstedge |
弧结点：
| 顶点域1 | ivex链域 | 顶点域2 | jvex链域 | 数据域 |
|---|---|---|---|---|
| ivex | ilink | jvex | jlink | info |
图：
横向的ivex相同，纵向的jvex相同
顺着ilink可以找到同意依附于ivex的下一条边，同理，顺着jlink可以找到同样依附于jvex的下一条边。