KMP算法讲解的很多,清晰的很少,在此写一个汪汪都能看懂的通俗易懂直观的精讲。文末会给出学习建议。
KMP算法的由来和本文术语解释
KMP算法的中文名称为快速模式匹配算法,是为了快速解决在一个字符串中查找另一个字符串的问题。(为了方便描述,要找到的那个字符串叫模式串,要搜索的那个范围叫文本串。比如要求在字符串abbaf中找到字符串baf,baf就是模式串,abbaf就是文本串)。
针对这种问题,我们其实很容易想到一种暴力的算法,那就是一个一个比。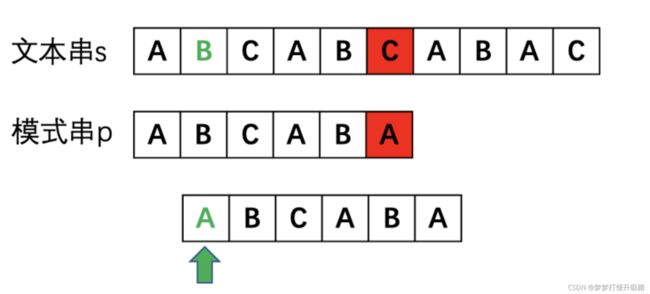
不难发现,遇到不匹配的情况时,模式串每次都是傻傻的挪一下,然后再一位一位地去比较。
暴力太傻了吧,所以就有了KMP算法,让模式串迈开腿,能够大步往前走。但大步走也不是瞎走,不然走过了相等的村就没有相等的店了,得有点策略地走,于是有了next数组。这个数组的名字起的其实还是有点形象的,代表比到某一位不匹配了下一个比哪一位,像一个指导手册似的。
为什么要有next数组以及对他的直观理解
next数组就是一个模式串的行为指导手册。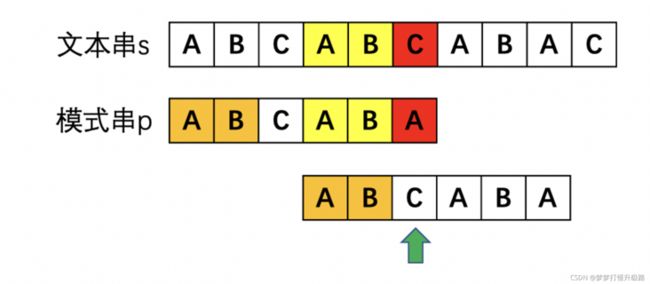
当红色的C和A不匹配时,黄色的AB和AB已经比较过了,而模式串p中橙色和黄色部分是相等的,那挺好,黄色AB都跟文本串比过了,橙色的AB就可以省点事,这样直接比较绿色箭头处就可以了。
那我们怎么决定从哪一位开始比较呢。这里就引入了前后缀的问题。要找到模式串p中不匹配位置A前面的子串"ABCAB"中相同的前缀和后缀,这个相同的部分就是可以偷懒不用比的部分了。那如果相同的前缀和后缀有很多取哪个呢?那肯定取最长的呀,这样就能偷更多懒,下一轮不用比的就更多了。
所以,为了知道如何偷懒,我们定义了一个没有名字的表,这个表告诉我们以某个位置的字符结尾的字符串,最长的相同前后缀的长度是多少。
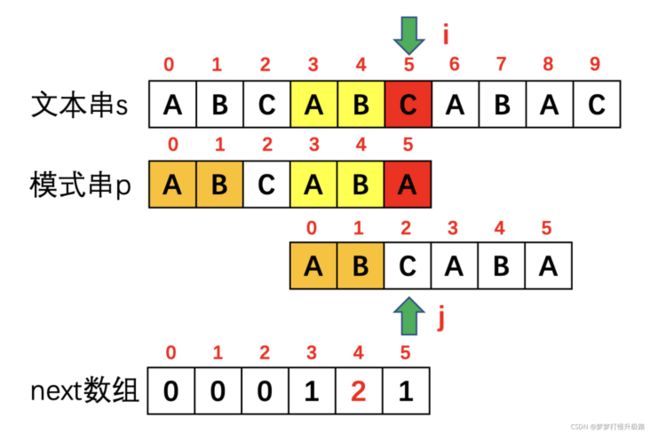
那为啥要知道长度呢?长度其实就是下一次的下标。以下图为例,A前面以B为结尾的字符串ABCAB的最长相同前后缀的长度为2,那下一轮比较的就是2位置的C,前面的不用比了。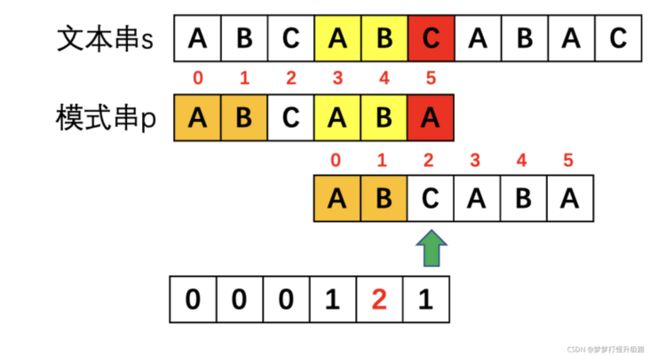
那么这个时候next数组就出场了,他就和这个不知名的表有关系,但又不完全一样,但本质上next都是由这张表变来的。
实际实现时根据需要可能把这个表的所有元素-1,也可能所有元素右移之类的(右移的话AC不匹配时就不用看前一位的next了,直接看自己位置的就行,因为别人的右移到自己的地盘了)。我也不知道为啥就要-1之类的,除了让KMP更难理解以外,好像啥用没有。
本文就不进行这些花里胡哨的操作了。
精华!next数组的代码实现 图预警
到现在大部分人估计都能手写一个模式串的next的数组了,毕竟肉眼看最长的相同前后缀也还行。但是看到代码实现的时候还是会懵的不行,这是因为真的太巧妙了,其中甚至用到了递归的思路。为了好理解,我就直接将前文图中推导的表作为next数组。
递归思路如何画图理解
1.定义两个指针,cur是指向当前位置的,代表要求以cur位置字符结尾的最长相同前后缀,recur有两个含义,可能是上一轮循环之后传过来的(代表以前一个字符结尾的最长相同前后缀),也可能是递归的时候递归到的,反正也不用管这么多,反正recur在赋值给next时候就会指向最长相同前缀的下一位。
2.画图理解递归的思路
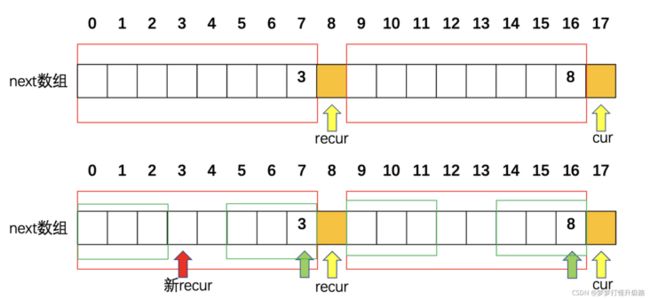
如图显示的是进入某一轮循环,cur=17,recur=8时递归代码的执行过程。
next[cur-1]= next[16] = 8代表红色的两个框相同(时刻牢记next的含义)
- 如果这个时候s[cur] == s[recur]说明next[cur] = recur+1=9,表示最长相同前后缀长度为9。
- 如果这个时候s[cur] != s[recur]说明next[cur] <= recur,这里就要用到递归了。红色框中字符相等,我们求的最长相同后缀是以cur结尾的那一撮,那就可以转化为求recur-1结尾的最长相同前后缀,即next[recur-1]。根据next[recur-1]=next[7]的值3可以知道左边两个绿框相同,所以图中四个绿框就都相同了。但是咱要的其实还是左右边上的两个绿框相等。
- 接下来就还是循环第一步,recur指针移到新的红色位置。如果这时next[cur] == next[recur]的话,next[cur] = recur+1=4。如果不相等,那recur还要递归移动,直到recur = 0时不能再移动或者遇到相等的情况。
void getNext(int* next,string& s){
int recur = 0;
next[0] = recur;
for(int cur = 1;cur < s.size();cur++){
while(recur > 0 && s[cur] != s[recur]){
recur = next[recur-1];//递归部分
}
if(s[cur] == s[recur]){//recur=0或者相等的时候
recur++;
}
next[cur] = recur;
}
}计算next时初始化值如何确定
另外,代码的初始条件也不能看着答案想当然。next[0]=0是因为只有s[0]一个元素时,不存在最长相同前后缀。j的初始化有两种办法可以考虑,一种是观察for循环中的next[i]=j,所以next[0]=0时j就是0。也可以在计算next[1]的时候看看,需要j是几才能得到正确答案。
计算结果的图形化解释
KMP算法的代码实现
利用next实现KMP的关键要点
有了next数组之后,如何利用他呢?大体来说是控制模式串指针和文本串指针的移动,直到到达文本串末尾或者模式串末尾。其中有以下几个要点:
- 遇到某一位不匹配时,要根据这一位前一位的next值确认接下来要比较的是模式串中的哪一位(也就是模式串指针指向哪里)。
- 1中改变了模式串指针之后,文本串指针不能移动到下一位,而是要保持不变,继续比较,否则就会越过一些值。所以for内部需要有while循环,而不能写if让其进入下一轮for循环。
int j = 0;
for(int i = 0;i < haystack.size();i++){
while(j > 0 && needle[j] != haystack[i]){//对应要点2的while循环
cout << "pattern[" << j << "]" << "!=" << "s[" << i << "]" << endl;
cout << "j从" << j << "变为" << next[j-1] << endl;
j = next[j-1];//对应要点1的找前一位
}
if(needle[j] == haystack[i]){
cout << "pattern[" << j << "]" << "==" << "s[" << i << "]" << endl;
j++;
}
if(j == needle.size()) return i - needle.size()+1;//结束坐标-长度+1=起始坐标
}运行结果的图形化解释
加入必要的注释运行,结果如下,与图片完全对应。
pattern[0]==s[0]
pattern[1]==s[1]
pattern[2]==s[2]
pattern[3]==s[3]
pattern[4]==s[4]
pattern[5]!=s[5]
j从5变为2
pattern[2]==s[5]
pattern[3]==s[6]
pattern[4]==s[7]
pattern[5]==s[8]最后的学习建议
找个很长的字符串,按我的推导把getNext函数人工推导一次,这样就拿理解recur变化的巧妙之处了。当递归不好理解时,一定要结合解释递归的那两个红框和绿框去思考。