吴恩达《神经网络和深度学习》第二周编程作业—用神经网络思想实现逻辑回归
吴恩达《神经网络和深度学习》—用神经网络思想实现逻辑回归
- 1 安装包
- 2 问题概述
- 3 学习算法的一般架构
- 4 构建算法的各个部分
-
- 4.1 激活函数
- 4.2 初始化参数
- 4.3 前向和后向传播
- 4.4 使用梯度下降算法更新学习参数
- 4.5 预测
- 5 将所有功能合并到模型中
- 6 学习率的选择
- 7 使用自己的图像进行测试
※※※※※上一篇:【numpy入门,函数向量化实现】※※※※※下一篇:【用一层隐藏层的神经网络分类二维数据】※※※※※
做完该作业将掌握的技能:
∙ \bullet ∙ 建立学习算法的一般架构,包括:
(1)初始化参数
(2)计算损失函数及其梯度
(3)使用优化算法(梯度下降)
∙ \bullet ∙ 按正确的顺序将以上所有三个功能集成到一个主模型上。
本文所使用的资料:【点击下载】,提取码:xoyp。请在开始之前下载好所需资料,然后将文件解压到你的代码文件同一级目录下,请确保你的代码那里有lr_utils.py和datasets文件夹。
1 安装包
我们要做的事是搭建一个能够【识别猫】的简单的神经网络,在开始之前,我们需要引入以下相关库:
∙ \bullet ∙ numpy:是Python科学计算的基本包。
∙ \bullet ∙ h5py:是一个常用的包,可以处理存储为H5文件格式的数据集。
∙ \bullet ∙ matplotlib:是一个著名的Python图形库。
∙ \bullet ∙ lr_utils:在本文的资料包里,一个加载资料包里面的数据的简单功能的库。
如果你没有以上的库,请自行安装,并且在需要时按如下方式加载到程序中。
import numpy as np
import matplotlib.pyplot as plt
import h5py
from lr_utils import load_dataset
2 问题概述
datasets文件夹下包含以下内容的数据集:
∙ \bullet ∙ 标记为cat(y = 1)或非cat(y = 0)的m_train训练图像集
∙ \bullet ∙ 标记为cat或non-cat的m_test测试图像集
∙ \bullet ∙ 图像维度为(num_px,num_px,3),其中3表示3个通道(RGB)。 因此,每个图像都是正方形(高度= num_px)和(宽度= num_px)。
基于该数据集,我们将构建一个简单的图像识别算法,该算法可以将图片正确分类为猫和非猫。
首先,熟悉一下数据集, 通过运行以下代码来加载数据。
# Loading the data (cat/non-cat)
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
其中,load_dataset()函数的定义在lr_utils.py中,源代码如下所示:
【代码】:
import numpy as np
import h5py
def load_dataset():
train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
classes = np.array(test_dataset["list_classes"][:]) # the list of classes
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes
【说明】:
∙ \bullet ∙ train_set_x_orig:保存的是训练集里面的图像数据(本训练集有209张64x64的图像)。
∙ \bullet ∙ train_set_y_orig:保存的是训练集的图像对应的分类值(【0 | 1】,0表示不是猫,1表示是猫)。
∙ \bullet ∙ test_set_x_orig:保存的是测试集里面的图像数据(本训练集有50张64x64的图像)。
∙ \bullet ∙ test_set_y_orig:保存的是测试集的图像对应的分类值(【0 | 1】,0表示不是猫,1表示是猫)。
∙ \bullet ∙ classes:保存的是以bytes类型保存的两个字符串数据,数据为:[b’non-cat’ b’cat’]。
我们还可以看一下我们加载的文件里面的图片都是些什么样子的,比如查看一下训练集里面的第50张图片,当然你也可以改变index的值查看一下其他的图片。
【代码】:
# Example of a picture
index = 50
# 打印出当前的训练标签值
# 使用np.squeeze的目的是压缩维度,【未压缩】train_set_y[:,index]的值为[1] , 【压缩后】np.squeeze(train_set_y[:,index])的值为1
# print("【使用np.squeeze:" + str(np.squeeze(train_set_y[:,index])) + ",不使用np.squeeze: " + str(train_set_y[:,index]) + "】")
# 只有压缩后的值才能进行解码操作
print("y = " + str(train_set_y[:, index]) + ", it's a '" + classes[np.squeeze(train_set_y[:, index])].decode("utf-8") + "' picture.")
plt.imshow(train_set_x_orig[index])
plt.show()
【结果】:
y = [1], it's a 'cat' picture.
深度学习中的许多报错都来自于矩阵/向量尺寸不匹配。如果你可以保持矩阵/向量的尺寸不变,那么将消除大多错误。
【练习】:获取以下各项的值:
∙ \bullet ∙ m_train:训练集里图片的数量
∙ \bullet ∙ m_test:测试集里图片的数量
∙ \bullet ∙ num_px: 训练、测试集里面的图片的宽度和高度(均为64x64)。
请记住,train_set_x_orig是一个维度为(m_train, num_px, num_px, 3)的numpy数组。例如,你可以通过编写train_set_x_orig.shape[0]来访问m_train。
【代码】:
m_train = train_set_x_orig.shape[0] # 训练集里图片的数量。
m_test = test_set_x_orig.shape[0] # 测试集里图片的数量。
num_px = train_set_x_orig.shape[1] # 训练、测试集里面的图片的宽度和高度(均为64x64)。
# 现在看一看我们加载的东西的具体情况
print ("训练集的数量: m_train = " + str(m_train))
print ("测试集的数量 : m_test = " + str(m_test))
print ("每张图片的宽/高 : num_px = " + str(num_px))
print ("每张图片的大小 : (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("训练集_图片的维数 : " + str(train_set_x_orig.shape))
print ("训练集_标签的维数 : " + str(train_set_y.shape))
print ("测试集_图片的维数: " + str(test_set_x_orig.shape))
print ("测试集_标签的维数: " + str(test_set_y.shape))
【结果】:
训练集的数量: m_train = 209
测试集的数量 : m_test = 50
每张图片的宽/高 : num_px = 64
每张图片的大小 : (64, 64, 3)
训练集_图片的维数 : (209, 64, 64, 3)
训练集_标签的维数 : (1, 209)
测试集_图片的维数: (50, 64, 64, 3)
测试集_标签的维数: (1, 50)
为了方便,我们要把维度为(64,64,3)的numpy数组重新构造为(64 x 64 x 3,1)的数组,要乘以3的原因是每张图片是由64x64像素构成的,而每个像素点由(R,G,B)三原色构成的,所以要乘以3。在此之后,我们的训练和测试数据集是一个numpy数组,每列代表一个展平的图像,应该有m_train和m_test列。
【练习】:重塑训练和测试数据集,以便将大小(num_px,num_px,3)的图像展平为单个形状的向量(num_px ∗ \ast ∗ num_px ∗ \ast ∗ 3, 1)。
【说明】:当你想将维度为(a,b,c,d)的矩阵X展平为形状为(b ∗ \ast ∗c ∗ \ast ∗d, a)的矩阵X_flatten时的一个技巧是:
X_flatten = X.reshape(X.shape [0],-1).T # 其中X.T是X的转置矩阵
【代码】:
# Reshape the training and test examples
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
print("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print("train_set_y shape: " + str(train_set_y.shape))
print("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))
print("test_set_y shape: " + str(test_set_y.shape))
这一段意思是指把数组变为209行的矩阵(因为训练集里有209张图片),但是我懒得算列有多少,于是我就用-1告诉程序你帮我算,最后程序算出来是12288列,我再最后用一个T表示转置,这就变成了12288行,209列。测试集亦如此。
【结果】:
train_set_x_flatten shape: (12288, 209)
train_set_y shape: (1, 209)
test_set_x_flatten shape: (12288, 50)
test_set_y shape: (1, 50)
为了表示彩色图像,必须为每个像素指定红、绿、蓝色通道(RGB),因此像素值实际上是一个从0到255的三个数字的向量。机器学习中一个常见的预处理步骤是对数据集进行居中和标准化,这意味着可以减去每个示例中整个numpy数组的平均值,然后将每个示例除以整个numpy数组的标准偏差。但对于图片数据集,它更简单,更方便,几乎可以将数据集的每一行除以255(像素通道的最大值),因为在RGB中不存在比255大的数据,所以我们可以放心的除以255,让标准化的数据位于[0,1]之间,现在标准化我们的数据集:
【总结】:预处理数据集的常见步骤是:
∙ \bullet ∙ 找出数据的尺寸和维度(m_train,m_test,num_px等)
∙ \bullet ∙ 重塑数据集,以使每个示例都是大小为(num_px ∗ \ast ∗ num_px ∗ \ast ∗ 3,1)的向量
∙ \bullet ∙ “标准化”数据
3 学习算法的一般架构
预处理完完数据之后就可以开始来设计一种简单的算法来区分猫图像和非猫图像了。
我们将使用神经网络思维方式建立Logistic回归。下图说明了为什么逻辑回归实际上是一个非常简单的神经网络!
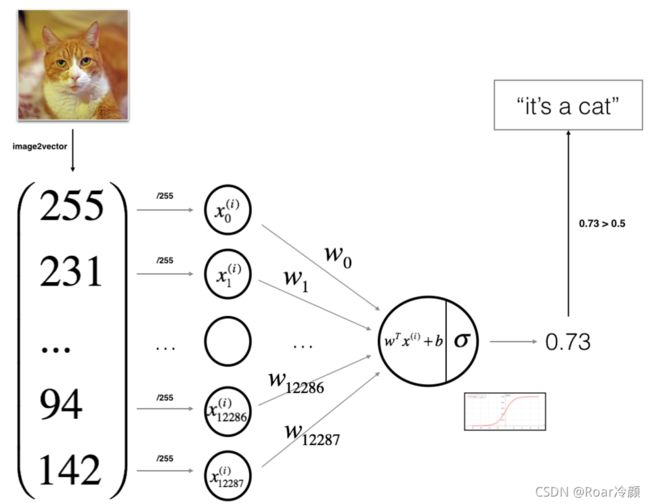
【算法的数学表达式】:
对于第 i i i 个样本 x ( i ) x^{\left ( i \right )} x(i):
z ( i ) = w T x ( i ) + b (1) z^{\left ( i \right )}=w^{T}x^{\left ( i \right )}+b \tag{1} z(i)=wTx(i)+b(1) y ^ ( i ) = a ( i ) = s i g m o i d ( z ( i ) ) (2) \hat{y}^{\left ( i \right )}=a^{\left ( i \right )}=sigmoid\left ( z^{\left ( i \right )} \right ) \tag{2} y^(i)=a(i)=sigmoid(z(i))(2) £ ( a ( i ) , y ( i ) ) = − y ( i ) l o g ( a ( i ) ) − ( 1 − y ( i ) ) l o g ( 1 − a ( i ) ) (3) \pounds \left ( a^{\left ( i \right )},\, y^{\left ( i \right )} \right ) = -y^{\left ( i \right )}log\left ( a^{\left ( i \right )} \right )-\left ( 1-y^{\left ( i \right )} \right )log\left ( 1-a^{\left ( i \right )} \right ) \tag{3} £(a(i),y(i))=−y(i)log(a(i))−(1−y(i))log(1−a(i))(3)
然后通过对所有训练样例求和来计算成本:
J = 1 m ∑ i = 1 m £ ( a ( i ) , y ( i ) ) (4) J = \frac{1}{m}\sum_{i=1}^{m}\pounds \left ( a^{\left ( i \right )},\, y^{\left ( i \right )} \right ) \tag{4} J=m1i=1∑m£(a(i),y(i))(4)
【关键步骤】:
∙ \bullet ∙ 初始化模型参数
∙ \bullet ∙ 通过最小化损失来学习模型的参数
∙ \bullet ∙ 使用学习到的参数进行预测(在测试集上)
∙ \bullet ∙ 分析结果并得出结论
4 构建算法的各个部分
【建立神经网络的主要步骤是】:
1. 定义模型结构(例如输入特征的数量)
2. 初始化模型的参数
3. 循环:
∙ \bullet ∙ 计算当前损失(正向传播)
∙ \bullet ∙ 计算当前梯度(向后传播)
∙ \bullet ∙ 更新参数(梯度下降)
我们通常会分别构建1-3,然后将它们集成到一个称为model()的函数中。
4.1 激活函数
现在构建sigmoid()函数,根据【算法的数学表达式】可知我们需要计算 s i g m o i d ( w T x + b ) = 1 1 + e − ( w T x + b ) sigmoid\left ( w^{T}x+b \right )=\frac{1}{1+e^{-\left ( w^{T}x+b \right )}} sigmoid(wTx+b)=1+e−(wTx+b)1来做出预测。可以使用np.exp()来实现。
【代码】:
# GRADED FUNCTION: sigmoid
def sigmoid(z):
"""
参数:
z -- 任何大小的标量或numpy数组。
返回:
s -- sigmoid(z)
"""
s = 1 / (1 + np.exp(-z))
return s
我们可以测试一下sigmoid(),检查一下是否符合我们所需要的条件。
【测试】:
# 测试sigmoid()
print("====================测试sigmoid====================")
print("sigmoid([0, 2]) = " + str(sigmoid(np.array([0,2]))))
【结果】:
====================测试sigmoid====================
sigmoid([0, 2]) = [0.5 0.88079708]
4.2 初始化参数
接下来,我们需要初始化参数 w w w 和 b b b,可以使用np.zeros()。
【代码】:
# GRADED FUNCTION: initialize_with_zeros
def initialize_with_zeros(dim):
"""
此函数为w创建一个维度为(dim,1)的0向量,并将b初始化为0。
参数:
dim -- 我们想要的w矢量的大小(或者这种情况下的参数数量)
返回:
w -- 维度为(dim,1)的初始化向量。
b -- 初始化的标量(对应于偏差)
"""
w = np.zeros(shape=(dim, 1))
b = 0
# 使用断言来确保我要的数据是正确的
assert (w.shape == (dim, 1)) # w的维度是(dim,1)
assert (isinstance(b, float) or isinstance(b, int)) # b的类型是float或者是int
return w, b
同样,我们可以测试一下initialize_with_zeros(dim),检查一下是否符合我们所需要的条件。
【测试】:
# 测试initialize_with_zeros(dim)
print("====================测试initialize_with_zeros(dim)====================")
dim = 2
w, b = initialize_with_zeros(dim)
print("w = " + str(w))
print("b = " + str(b))
====================测试initialize_with_zeros(dim)====================
w = [[0.]
[0.]]
b = 0
对于图像输入, w w w 的维度为(num_px ∗ \ast ∗ num_px ∗ \ast ∗ 3,1)。
4.3 前向和后向传播
现在,参数已初始化,接下来可以执行“向前”和“向后”传播步骤来学习参数。
【前向传播】:
∙ \bullet ∙ 构建样本矩阵 X X X
∙ \bullet ∙ 计算 A = σ ( w T X + b ) = ( a ( 1 ) , a ( 2 ) , ⋯ , a ( m ) ) A = \sigma \left ( w^{T}X + b \right )=\left ( a^{\left ( 1 \right )},\, a^{\left ( 2 \right )},\cdots ,a^{\left ( m \right )} \right ) A=σ(wTX+b)=(a(1),a(2),⋯,a(m))
∙ \bullet ∙ 计算损失函数: J = − 1 m ∑ i = 1 m y ( i ) l o g ( a ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − a ( i ) ) J =-\frac{1}{m}\sum_{i=1}^{m} y^{\left ( i \right )}log\left ( a^{\left ( i \right )} \right )+\left ( 1-y^{\left ( i \right )} \right )log\left ( 1-a^{\left ( i \right )} \right ) J=−m1i=1∑my(i)log(a(i))+(1−y(i))log(1−a(i))
【后向传播】:
∂ J ∂ w = 1 m X ( A − Y ) T (5) \frac{\partial J}{\partial w}=\frac{1}{m}X\left ( A-Y \right )^{T} \tag{5} ∂w∂J=m1X(A−Y)T(5) ∂ J ∂ b = 1 m ∑ i = 1 m ( a ( i ) − y ( i ) ) (6) \frac{\partial J}{\partial b}=\frac{1}{m}\sum_{i=1}^{m}\left ( a^{\left ( i \right )}- y^{\left ( i \right )}\right ) \tag{6} ∂b∂J=m1i=1∑m(a(i)−y(i))(6)
首先,我们需要实现函数propagate()来计算损失函数及其梯度。
【代码】:
# GRADED FUNCTION: propagate
def propagate(w, b, X, Y):
"""
实现前向和后向传播的成本函数及其梯度。
参数:
w -- 权重,大小不等的数组(num_px * num_px * 3,1)
b -- 偏差,一个标量
X -- 矩阵类型为(num_px * num_px * 3,训练数量)
Y -- 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据数量)
返回:
cost -- 逻辑回归的负对数似然成本
dw -- 相对于w的损失梯度,因此与w相同的形状
db -- 相对于b的损失梯度,因此与b的形状相同
"""
m = X.shape[1]
# 正向传播
A = sigmoid(np.dot(w.T, X) + b) # 计算激活值,请参考公式2。
cost = (- 1 / m) * np.sum(Y * np.log(A) + (1 - Y) * (np.log(1 - A))) # 计算成本,请参考公式3和4。
# 反向传播
dw = (1 / m) * np.dot(X, (A - Y).T) # 请参考视频中的偏导公式。
db = (1 / m) * np.sum(A - Y) # 请参考视频中的偏导公式。
# 使用断言确保我的数据是正确的
assert (dw.shape == w.shape)
assert (db.dtype == float)
cost = np.squeeze(cost)
assert (cost.shape == ())
# 创建一个字典,把dw和db保存起来。
grads = {
"dw": dw,
"db": db
}
return grads, cost
【测试】:写好之后我们来测试一下。
# 测试一下propagate
print("====================测试propagate====================")
# 初始化一些参数
w, b, X, Y = np.array([[1], [2]]), 2, np.array([[1, 2], [3, 4]]), np.array([[1, 0]])
grads, cost = propagate(w, b, X, Y)
print("dw = " + str(grads["dw"]))
print("db = " + str(grads["db"]))
print("cost = " + str(cost))
【结果】:
====================测试propagate====================
dw = [[0.99993216]
[1.99980262]]
db = 0.49993523062470574
cost = 6.000064773192205
4.4 使用梯度下降算法更新学习参数
接下来,我们需要编写优化函数optimize(),其原理为使用梯度下降算法更新学习参数,即通过最小化成本函数 J J J 来学习 w w w 和 b b b。对于参数 θ \theta θ,更新规则为 θ = θ − α d θ \theta = \theta - \alpha d\theta θ=θ−αdθ,其中 α \alpha α 为学习率。
【代码】:
# GRADED FUNCTION: optimize
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost=False):
"""
此函数通过运行梯度下降算法来优化w和b
参数:
w -- 权重,大小不等的数组(num_px * num_px * 3,1)
b -- 偏差,一个标量
X -- 维度为(num_px * num_px * 3,训练数据的数量)的数组。
Y -- 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据的数量)
num_iterations -- 优化循环的迭代次数
learning_rate -- 梯度下降更新规则的学习率
print_cost -- 每100步打印一次损失值
返回:
params -- 包含权重w和偏差b的字典
grads -- 包含权重和偏差相对于成本函数的梯度的字典
costs -- 优化期间计算的所有成本列表,将用于绘制学习曲线。
提示:
我们需要写下两个步骤并遍历它们:
1)计算当前参数的成本和梯度,使用propagate()。
2)使用w和b的梯度下降法则更新参数。
"""
costs = []
for i in range(num_iterations):
grads, cost = propagate(w, b, X, Y)
dw = grads["dw"]
db = grads["db"]
w = w - learning_rate * dw
b = b - learning_rate * db
# 记录成本
if i % 100 == 0:
costs.append(cost)
# 打印成本数据
if (print_cost) and (i % 100 == 0):
print("迭代的次数: %i , 误差值: %f" % (i, cost))
params = {
"w": w,
"b": b}
grads = {
"dw": dw,
"db": db}
return params, grads, costs
【测试】:写好之后我们来测试一下优化函数:
# 测试optimize
print("====================测试optimize====================")
w, b, X, Y = np.array([[1], [2]]), 2, np.array([[1, 2], [3, 4]]), np.array([[1, 0]])
params, grads, costs = optimize(w, b, X, Y, num_iterations=100, learning_rate=0.009, print_cost=False)
print("w = " + str(params["w"]))
print("b = " + str(params["b"]))
print("dw = " + str(grads["dw"]))
print("db = " + str(grads["db"]))
print(costs)
【结果】:
====================测试optimize====================
w = [[0.1124579 ]
[0.23106775]]
b = 1.5593049248448891
dw = [[0.90158428]
[1.76250842]]
db = 0.4304620716786828
[6.000064773192205]
4.5 预测
optimize()函数会输出已学习的 w w w 和 b b b 的值,我们可以使用 w w w 和 b b b 来预测数据集 X X X 的标签。
现在我们要实现预测函数predict()。计算预测有两个步骤:
∙ \bullet ∙ 计算 Y ^ = A = σ ( w T X + b ) \hat{Y}=A=\sigma\left ( w^{T}X+b \right ) Y^=A=σ(wTX+b)
∙ \bullet ∙ 将 a a a 的项转换为0(如果激活<= 0.5)或1(如果激活> 0.5),并将预测结果存储在向量Y_prediction中。
【代码】:
# GRADED FUNCTION: predict
def predict(w, b, X):
"""
使用学习逻辑回归参数logistic (w,b)预测标签是0还是1,
参数:
w -- 权重,大小不等的数组(num_px * num_px * 3,1)
b -- 偏差,一个标量
X -- 维度为(num_px * num_px * 3,训练数据的数量)的数据
返回:
Y_prediction - 包含X中所有图片的所有预测【0 | 1】的一个numpy数组(向量)
"""
m = X.shape[1] # 图片的数量
Y_prediction = np.zeros((1, m))
w = w.reshape(X.shape[0], 1)
# 预测猫在图片中出现的概率
A = sigmoid(np.dot(w.T, X) + b)
for i in range(A.shape[1]):
# 将概率a [0,i]转换为实际预测p [0,i]
Y_prediction[0, i] = 1 if A[0, i] > 0.5 else 0
# 使用断言
assert (Y_prediction.shape == (1, m))
return Y_prediction
【测试】:同样,我们来测试一下。
# 测试predict
print("====================测试predict====================")
w, b, X, Y = np.array([[1], [2]]), 2, np.array([[1, 2], [3, 4]]), np.array([[1, 0]])
print("predictions = " + str(predict(w, b, X)))
【结果】:
====================测试predict====================
predictions = [[1. 1.]]
至此,我们已经实现了以下几个函数:
1. 初始化 ( w , b ) (w,b) (w,b)
2. 迭代优化损失以学习参数 ( w , b ) (w,b) (w,b) :
∙ \bullet ∙ 计算损失及其梯度
∙ \bullet ∙ 使用梯度下降更新参数
3. 使用学到的 ( w , b ) (w,b) (w,b) 来预测给定示例集的标签
5 将所有功能合并到模型中
就目前而言,我们基本上把所有的东西都做完了,现在我们要把这些函数统统整合到一个model()函数中,届时只需要调用一个model()就基本上完成所有的事了。
【代码】:
# GRADED FUNCTION: model
def model(X_train, Y_train, X_test, Y_test, num_iterations=2000, learning_rate=0.5, print_cost=False):
"""
通过调用之前实现的函数来构建逻辑回归模型
参数:
X_train -- numpy的数组,维度为(num_px * num_px * 3,m_train)的训练集
Y_train -- numpy的数组,维度为(1,m_train)(矢量)的训练标签集
X_test -- numpy的数组,维度为(num_px * num_px * 3,m_test)的测试集
Y_test -- numpy的数组,维度为(1,m_test)的(向量)的测试标签集
num_iterations -- 表示用于优化参数的迭代次数的超参数
learning_rate -- 表示optimize()更新规则中使用的学习速率的超参数
print_cost -- 设置为true以每100次迭代打印成本
返回:
d - 包含有关模型信息的字典。
"""
w, b = initialize_with_zeros(X_train.shape[0])
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
# 从字典“参数”中检索参数w和b
w, b = parameters["w"], parameters["b"]
# 预测测试/训练集的例子
Y_prediction_test = predict(w, b, X_test)
Y_prediction_train = predict(w, b, X_train)
# 打印训练后的准确性
print("训练集准确性:", format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100), "%")
print("测试集准确性:", format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100), "%")
d = {
"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediciton_train": Y_prediction_train,
"w": w,
"b": b,
"learning_rate": learning_rate,
"num_iterations": num_iterations}
return d
【测试】:把整个model()构建好之后我们就可以开始实际的测试了。
print("====================测试model====================")
# 这里加载的是真实的数据,请参见上面的代码部分。
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations=2000, learning_rate=0.005, print_cost=True)
【结果】:
====================测试model====================
迭代的次数: 0 , 误差值: 0.693147
迭代的次数: 100 , 误差值: 0.584508
迭代的次数: 200 , 误差值: 0.466949
迭代的次数: 300 , 误差值: 0.376007
迭代的次数: 400 , 误差值: 0.331463
迭代的次数: 500 , 误差值: 0.303273
迭代的次数: 600 , 误差值: 0.279880
迭代的次数: 700 , 误差值: 0.260042
迭代的次数: 800 , 误差值: 0.242941
迭代的次数: 900 , 误差值: 0.228004
迭代的次数: 1000 , 误差值: 0.214820
迭代的次数: 1100 , 误差值: 0.203078
迭代的次数: 1200 , 误差值: 0.192544
迭代的次数: 1300 , 误差值: 0.183033
迭代的次数: 1400 , 误差值: 0.174399
迭代的次数: 1500 , 误差值: 0.166521
迭代的次数: 1600 , 误差值: 0.159305
迭代的次数: 1700 , 误差值: 0.152667
迭代的次数: 1800 , 误差值: 0.146542
迭代的次数: 1900 , 误差值: 0.140872
训练集准确性: 99.04306220095694 %
测试集准确性: 70.0 %
【分析】:
训练准确性接近100%。 这是一个很好的情况:你的模型正在运行,并且具有足够的容量来适合训练数据。 测试误差为70%。 考虑到我们使用的数据集很小,并且逻辑回归是线性分类器,对于这个简单的模型来说,这实际上还不错。
使用下面的代码(并更改index变量),你可以查看测试集图片上的预测。
【测试】:
# Example of a picture that was wrongly classified.
index = 1
print("y = " + str(test_set_y[0, index]) + ", you predicted that it is a \"" +
classes[int(d["Y_prediction_test"][0, index])].decode("utf-8") + "\" picture.")
plt.imshow(test_set_x[:, index].reshape((num_px, num_px, 3)))
plt.show()
【结果】:
y = 1, you predicted that it is a "cat" picture.
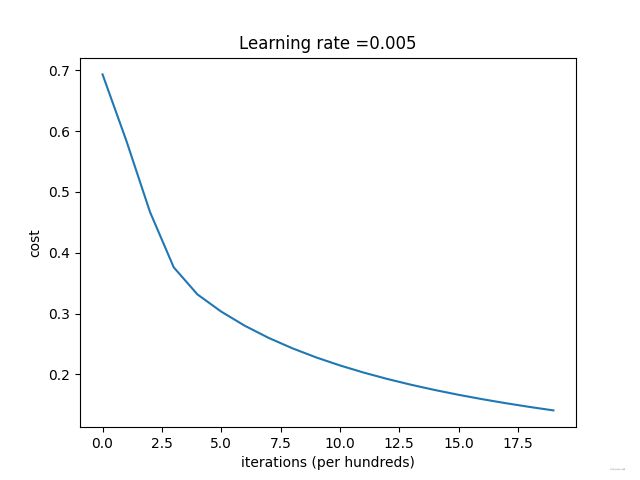
最后,我们可以绘制一下成本函数的变化趋势,从而直观的看出学习效果:
【代码】:
# Plot learning curve (with costs)
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()
损失下降表明正在学习参数。但是,你看到可以在训练集上训练更多模型。我们更改一下学习率和迭代次数,有可能会发现训练集的准确性可能会提高,但是测试集准确性会下降,这是由于过拟合造成的,但是我们并不需要担心,我们以后会使用更好的算法来解决这些问题的。
6 学习率的选择
为了使梯度下降起作用,你必须明智地选择学习率 α \alpha α。学习率决定我们更新参数的速度。 如果学习率太大,我们可能会“超出”最佳值。同样,如果太小,将需要更多的迭代才能收敛到最佳值。 这也是为什么调整好学习率至关重要。
我们可以比较一下我们模型的学习曲线和几种学习速率的选择。也可以尝试使用不同于我们初始化的learning_rates变量包含的三个值,并看一下会发生什么。
【代码】:
learning_rates = [0.01, 0.001, 0.0001]
models = {
}
for i in learning_rates:
print("learning rate is: " + str(i))
models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y,
num_iterations=1500, learning_rate=i, print_cost=False)
print('\n' + "-------------------------------------------------------" + '\n')
for i in learning_rates:
plt.plot(np.squeeze(models[str(i)]["costs"]), label=str(models[str(i)]["learning_rate"]))
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()
【结果】:
learning rate is: 0.01
训练集准确性: 99.52153110047847 %
测试集准确性: 68.0 %
-------------------------------------------------------
learning rate is: 0.001
训练集准确性: 88.99521531100478 %
测试集准确性: 64.0 %
-------------------------------------------------------
learning rate is: 0.0001
训练集准确性: 68.42105263157895 %
测试集准确性: 36.0 %
-------------------------------------------------------
【分析】:
1. 不同的学习率会带来不同的损失,因此会有不同的预测结果。
2. 如果学习率太大(0.01),则成本可能会上下波动。它甚至可能会发散(尽管在此示例中,使用0.01最终仍会以较高的损失值获得收益)。
3. 较低的损失并不意味着模型效果很好。当训练精度比测试精度高很多时,就会发生过拟合情况。
4. 在深度学习中,对于学习率的选择通常有以下建议:
∙ \bullet ∙ 选择好能最小化损失函数的学习率。
∙ \bullet ∙ 如果模型过度拟合,请使用其他方法来减少过度拟合。 (我们将在后面教程中讨论。)
【完整代码】:
# -*- coding: utf-8 -*-
"""
Created on Wed Nov 21 14:00:00 2021
博客地址 :https://blog.csdn.net/qq_29923461?spm=1018.2226.3001.5343&type=blog
@author: 冷颜
"""
import numpy as np
import matplotlib.pyplot as plt
import h5py
from lr_utils import load_dataset
train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = load_dataset()
m_train = train_set_y.shape[1] # 训练集里图片的数量。
m_test = test_set_y.shape[1] # 测试集里图片的数量。
num_px = train_set_x_orig.shape[1] # 训练、测试集里面的图片的宽度和高度(均为64x64)。
# 现在看一看我们加载的东西的具体情况
print ("训练集的数量: m_train = " + str(m_train))
print ("测试集的数量 : m_test = " + str(m_test))
print ("每张图片的宽/高 : num_px = " + str(num_px))
print ("每张图片的大小 : (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("训练集_图片的维数 : " + str(train_set_x_orig.shape))
print ("训练集_标签的维数 : " + str(train_set_y.shape))
print ("测试集_图片的维数: " + str(test_set_x_orig.shape))
print ("测试集_标签的维数: " + str(test_set_y.shape))
# 将训练集的维度降低并转置。
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
# 将测试集的维度降低并转置。
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
print("训练集降维最后的维度: " + str(train_set_x_flatten.shape))
print("训练集_标签的维数 : " + str(train_set_y.shape))
print("测试集降维之后的维度: " + str(test_set_x_flatten.shape))
print("测试集_标签的维数 : " + str(test_set_y.shape))
train_set_x = train_set_x_flatten / 255
test_set_x = test_set_x_flatten / 255
def sigmoid(z):
"""
参数:
z -- 任何大小的标量或numpy数组。
返回:
s -- sigmoid(z)
"""
s = 1 / (1 + np.exp(-z))
return s
def initialize_with_zeros(dim):
"""
此函数为w创建一个维度为(dim,1)的0向量,并将b初始化为0。
参数:
dim -- 我们想要的w矢量的大小(或者这种情况下的参数数量)
返回:
w -- 维度为(dim,1)的初始化向量。
b -- 初始化的标量(对应于偏差)
"""
w = np.zeros(shape=(dim, 1))
b = 0
# 使用断言来确保我要的数据是正确的
assert(w.shape == (dim, 1)) # w的维度是(dim,1)
assert(isinstance(b, float) or isinstance(b, int)) # b的类型是float或者是int
return w, b
def propagate(w, b, X, Y):
"""
实现前向和后向传播的成本函数及其梯度。
参数:
w -- 权重,大小不等的数组(num_px * num_px * 3,1)
b -- 偏差,一个标量
X -- 矩阵类型为(num_px * num_px * 3,训练数量)
Y -- 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据数量)
返回:
cost -- 逻辑回归的负对数似然成本
dw -- 相对于w的损失梯度,因此与w相同的形状
db -- 相对于b的损失梯度,因此与b的形状相同
"""
m = X.shape[1]
# 正向传播
A = sigmoid(np.dot(w.T, X) + b) # 计算激活值,请参考公式2。
cost = (- 1 / m) * np.sum(Y * np.log(A) + (1 - Y) * (np.log(1 - A))) # 计算成本,请参考公式3和4。
# 反向传播
dw = (1 / m) * np.dot(X, (A - Y).T) # 请参考视频中的偏导公式。
db = (1 / m) * np.sum(A - Y) # 请参考视频中的偏导公式。
# 使用断言确保我的数据是正确的
assert(dw.shape == w.shape)
assert(db.dtype == float)
cost = np.squeeze(cost)
assert(cost.shape == ())
# 创建一个字典,把dw和db保存起来。
grads = {
"dw": dw,
"db": db
}
return grads, cost
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost=False):
"""
此函数通过运行梯度下降算法来优化w和b
参数:
w -- 权重,大小不等的数组(num_px * num_px * 3,1)
b -- 偏差,一个标量
X -- 维度为(num_px * num_px * 3,训练数据的数量)的数组。
Y -- 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据的数量)
num_iterations -- 优化循环的迭代次数
learning_rate -- 梯度下降更新规则的学习率
print_cost -- 每100步打印一次损失值
返回:
params -- 包含权重w和偏差b的字典
grads -- 包含权重和偏差相对于成本函数的梯度的字典
成本 -- 优化期间计算的所有成本列表,将用于绘制学习曲线。
提示:
我们需要写下两个步骤并遍历它们:
1)计算当前参数的成本和梯度,使用propagate()。
2)使用w和b的梯度下降法则更新参数。
"""
costs = []
for i in range(num_iterations):
grads, cost = propagate(w, b, X, Y)
dw = grads["dw"]
db = grads["db"]
w = w - learning_rate * dw
b = b - learning_rate * db
# 记录成本
if i % 100 == 0:
costs.append(cost)
# 打印成本数据
if print_cost and (i % 100 == 0):
print("迭代的次数: %i , 误差值: %f" % (i, cost))
params = {
"w": w,
"b": b}
grads = {
"dw": dw,
"db": db}
return params, grads, costs
def predict(w, b, X):
"""
使用学习逻辑回归参数logistic (w,b)预测标签是0还是1,
参数:
w -- 权重,大小不等的数组(num_px * num_px * 3,1)
b -- 偏差,一个标量
X -- 维度为(num_px * num_px * 3,训练数据的数量)的数据
返回:
Y_prediction -- 包含X中所有图片的所有预测【0 | 1】的一个numpy数组(向量)
"""
m = X.shape[1] # 图片的数量
Y_prediction = np.zeros((1, m))
w = w.reshape(X.shape[0], 1)
# 预测猫在图片中出现的概率
A = sigmoid(np.dot(w.T, X) + b)
for i in range(A.shape[1]):
# 将概率a [0,i]转换为实际预测p [0,i]
Y_prediction[0, i] = 1 if A[0, i] > 0.5 else 0
# 使用断言
assert(Y_prediction.shape == (1, m))
return Y_prediction
def model(X_train, Y_train, X_test, Y_test, num_iterations=2000, learning_rate=0.5, print_cost=False):
"""
通过调用之前实现的函数来构建逻辑回归模型
参数:
X_train -- numpy的数组,维度为(num_px * num_px * 3,m_train)的训练集
Y_train -- numpy的数组,维度为(1,m_train)(矢量)的训练标签集
X_test -- numpy的数组,维度为(num_px * num_px * 3,m_test)的测试集
Y_test -- numpy的数组,维度为(1,m_test)的(向量)的测试标签集
num_iterations -- 表示用于优化参数的迭代次数的超参数
learning_rate -- 表示optimize()更新规则中使用的学习速率的超参数
print_cost -- 设置为true以每100次迭代打印成本
返回:
d -- 包含有关模型信息的字典。
"""
w, b = initialize_with_zeros(X_train.shape[0])
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
# 从字典“参数”中检索参数w和b
w, b = parameters["w"], parameters["b"]
# 预测测试/训练集的例子
Y_prediction_test = predict(w, b, X_test)
Y_prediction_train = predict(w, b, X_train)
# 打印训练后的准确性
print("训练集准确性:", format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100),"%")
print("测试集准确性:", format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100),"%")
d = {
"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediciton_train": Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate": learning_rate,
"num_iterations": num_iterations}
return d
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations=2000, learning_rate=0.005, print_cost=True)
# 绘制图
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()
7 使用自己的图像进行测试
最后,我们可以使用自己的图像并查看模型的预测输出,从而验证一下该模型。 要做到这一点:
1. 在源代码所在位置创建一个images文件夹,用于存放待测试的图片
2. 在以下代码中更改图像的名称
3. 运行代码,检查算法是否正确(1 = cat,0 = non-cat)
【代码】:
# image = "test2.jpg", 需要根据自己的文件名字进行修改
fname = 'my_images/test2.jpg'
image = np.array(plt.imread(fname))
size = (num_px, num_px, 3)
my_image = np.resize(image, size).reshape((1, num_px*num_px*3)).T # 重置原始图片的大小
my_predicted_image = predict(d["w"], d["b"], my_image)
print("y = " + str(np.squeeze(my_predicted_image)) + ", your algorithm predicts a \"" +
classes[int(np.squeeze(my_predicted_image)), ].decode("utf-8") + "\" picture.")
plt.imshow(image)
plt.show()
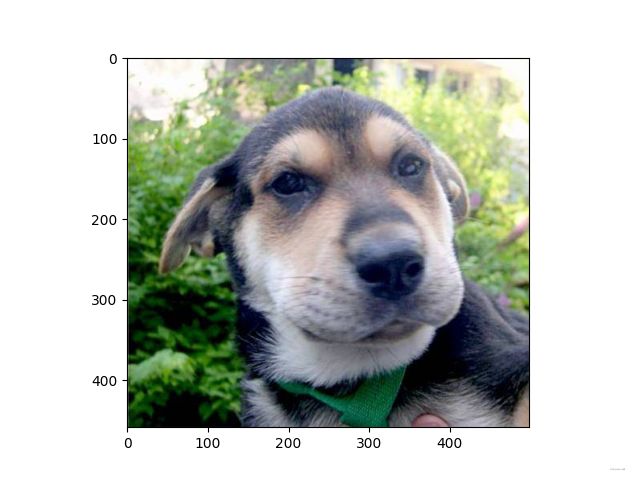
【结果】:我在images文件夹放置了两张测试图片,一张猫的图片,一张狗的图片,测试结果分别如下所示:
y = 1.0, your algorithm predicts a "cat" picture.
y = 0.0, your algorithm predicts a "non-cat" picture.
哈哈,测试结果还不错,大功告成!!!