r ridge回归_机器学习 | LASSO回归姊妹篇：R语言实现岭回归分析

作者：科研猫 | 西红柿

责编：科研猫 | 馋猫

前面的教程中，我们讲解了在高通量数据中非常常用的一种模型构建方法，LASSO 回归（见临床研究新风向，巧用LASSO回归构建属于你的心仪模型）。作为正则化方法的一种，除了LASSO，还有另外一种模型值得我们学习和关注，那就是岭回归（ridge regression）。今天，我们将简要介绍什么是岭回归，它能做什么和不能做什么。在岭回归中，范数项是所有系数的平方和，称为 L2-Norm。在回归模型中，我们试图最小化 RSS+λ (sumβj2)。随着λ增加，回归系数 β 减小，趋于 0，但从不等于 0。岭回归的优点是可以提高预测精度，但由于它不能使任何变量的系数等于零，很难满足减少变量个数的要求，因此在模型的可解释性方面会存在一些问题。为了解决这个问题，我们可以使用之前提到的 LASSO 回归。

此外，岭回归更常用于处理线性回归中的共线性问题。通常认为共线性会导致过度拟合，并且参数估计会非常大。因此，在回归系数β的最小二乘的目标函数中加入惩罚函数可以解决这个问题。正则化思想是一致的，因此岭回归可以解决这个问题。

案例分析

• 案例一

数据介绍

我们选择载入同 LASSO 回归一样的数据 Biopsy Data on Breast Cancer Patients。我们载入MASS 包中来自威斯康星乳腺癌患者的数据集。目的是确定活检结果是良性还是恶性。研究人员使用细针抽吸 (FNA) 技术收集样本并进行活检以确定诊断(恶性或良性)。我们的任务是开发尽可能精确的预测模型来确定肿瘤的性质。数据集包含 699 名患者的组织样本，并存储在包含 11 个变量的数据框中。此数据框包含以下列：

ID:  sample code number (not unique).
 V1:  clump thickness.
 V2:  uniformity of cell size.
 V3:  uniformity of cell shape.
 V4:  marginal adhesion.
 V5:  single epithelial cell size.
 V6:  bare nuclei (16 values are missing).
 V7:  bland chromatin.
 V8:  normal nucleoli.
 V9:  mitoses.
 class:  “benign” or “malignant”.

数据处理

我们首先加载 MASS 包并准备乳腺癌数据：

1library(glmnet)
2library(MASS)
3biopsy$ID =NULL
4names(biopsy) =c(“thick”, “u.size”, “u.shape”, “adhsn”, “s.size”, “nucl”, “chrom”, “n.nuc”, “mit”, “class”)
5biopsy.v2 <-na.omit(biopsy)
6set.seed(123) #random number generator
7ind<-sample(2, nrow(biopsy.v2), replace =TRUE, prob =c(0.7, 0.3))
8 train <-biopsy.v2[ind==1, ] #the training data set
9Convert data to generate input matrices and labels:
10x <-as.matrix(train[, 1:9])
11y <-train[, 10]

岭回归模型

我们首先使用岭回归建立模型，并将结果存储在对象 ridge 中。请注意：glmnet 包在计算lambda 值之前对输入值进行了标准化。我们需要将响应变量的分布指定为“二项式”，因为这是一个二进制结果；同时指定 alpha = 0 来表示此时的岭回归。R 代码如下：

1ridge <- glmnet(x, y, family = "binomial", alpha = 0)

此对象包含评估模型所需的所有信息。要做的第一件事是使用 print() 函数，该函数显示非零回归系数的值，解释百分比偏差或相应的 lambda 值。包中的默认计算数为 100，但是如果两个lambda 值的百分比偏差的改善不明显，则算法将在 100 次计算之前停止。换句话说，算法将收敛到最优解。

1  ## [100,] 9 8.389e-01 0.03951

以第 100 行为例，可以看出非零回归系数，即模型中包含的特征数为 9。在岭回归中，这个数字是常数。你还可以看到解释偏差的百分比是 0.8389，调协系数是 0.03951，但为了简单起见，我们将测试集的 lambda 设置为 0.05。

那么，让我们以图形的方式来看看回归系数是如何随 lambda 的变化而变化的。只需将参数xvar=“lambda” 添加到 plot() 函数中。

1  plot(ridge, xvar = “lambda”, label = TRUE)

此图显示当 lambda 下降时，压缩参数减小，但绝对系数增加。要查看特定值处 lambda 的系数，请使用 predict() 函数。现在，让我们看看当 λ 为 0.05 时，系数是多少。我们指定参数s = 0.05 和参数 type = “coefficients”。glmnet() 函数配置为在拟合模型时使用特定于 lambda 的值，而不是从 lambda 特定的两边插入值。R代码如下：

1  ridge.coef <- predict(ridge, s=0.05, type = “coefficients”)
ridge.coef

可以看出，对于所有的特征都得到了一个非零的回归系数。接下来，我们在将测试集转换为矩阵形式，就像我们在训练集中所做的那样：

1  newx <- as.matrix(test[, 1:9])

然后使用 predict() 函数构建一个名为 ridge.y 的对象，指定参数 type=“response” 和 lambda 值为 0.05

1  ridge.y <- predict(ridge, newx = newx, type = “response”, s=0.05)

通过计算误差和 AUC，我们可以看到该模型在测试集上的性能：

1   library(InformationValue)
2actuals <- ifelse(test$class == "malignant", 1, 0)
3misClassError(actuals, ridge.y )
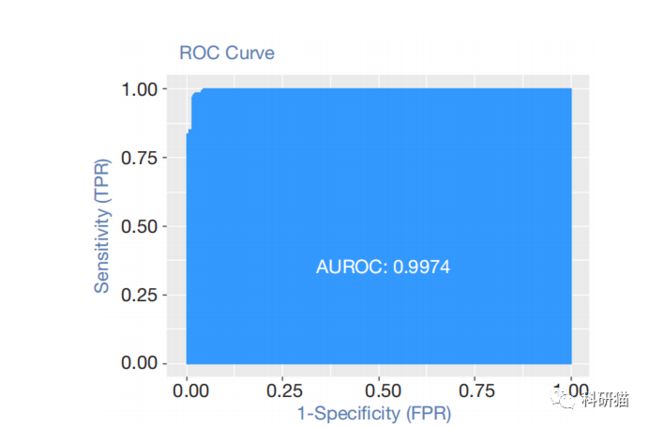
4plotROC(actuals, ridge.y)

该误分类率仅为 0.0191，表明该模型具有较高的分类和预测能力。

• 案例二

数据介绍

案例 2 是一个前列腺癌的数据。虽然这个数据集相对较小，只有 97 个观测值和 9 个变量，但与传统方法相比，这足以让我们掌握正则化方法。斯坦福大学医学中心为 97 名接受根治性前列腺切除术的患者提供了前列腺特异性抗原 (PSA) 数据。我们的目标是建立一个预测模型，利用来自临床测试的数据预测术后 PSA 水平。在预测患者术后能否恢复时，PSA 可能是一个比其他变量更有效的预后变量。手术后，医生会每隔一段时间检查患者的 PSA 水平，通过各种公式判断患者是否康复。术前预测模型和术后数据(此处未提供)共同改善前列腺癌的诊断和预后。从 97 名男性收集的数据集存储在包含 10 个变量的数据框中，如下所示：

 1  lcavol：肿瘤体积的对数；
 2  lweight：前列腺重量的对数；
 3  age：患者年龄(岁)；
 4  lbph：良性前列腺增生（BPH）、非癌性前列腺增生的对数；
 5  svi：是否侵犯精囊，表明癌细胞是否通过前列腺壁侵入精囊（1=是，0=否）；
 6  lcp：包膜穿透的对数，表示癌细胞扩散到前列腺包膜外的程度；
 7  Gleason：患者的Gleason评分。由病理学家在活检后给出，表明癌细胞的变异程度。分数越高，疾病危险度越大；
 8  pgg45：Gleason分数的百分比为4或5；
 9  lpsa：PSA值的对数值，这是结果变量；
 10 train：一个逻辑向量(TRUE或FALSE，用以区分训练数据集和测试数据集)。

数据处理

这个数据集包含在 R 的 ElemStatLearn 包中。加载所需的包和数据集。也可以找我们的工作人员领取。

 1 library(glmnet) 
 2 library(caret) 
 3 prostate <- load("prostate.RData")
 4 str(prostate)
 5 ## ‘data.frame’:    97 obs. of  10 variables:
 6 ##  $ lcavol : num  -0.58 -0.994 -0.511 -1.204 0.751 ...
 7 ##  $ lweight: num  2.77 3.32 2.69 3.28 3.43 ...
 8 ##  $ age    : int  50 58 74 58 62 50 64 58 47 63 ...
 9 ##  $ lbph   : num  -1.39 -1.39 -1.39 -1.39 -1.39 ...
10 ##  $ svi    : int  0 0 0 0 0 0 0 0 0 0 ...
11 ##  $ lcp    : num  -1.39 -1.39 -1.39 -1.39 -1.39 ...
12 ##  $ gleason: int  6 6 7 6 6 6 6 6 6 6 ...
13 ##  $ pgg45  : int  0 0 20 0 0 0 0 0 0 0 ...
14 ##  $ lpsa   : num  -0.431 -0.163 -0.163 -0.163 0.372 ...
15 ##  $ train  : logi  TRUE TRUETRUETRUETRUETRUE ...

在检查数据结构时，需要考虑一些问题。svi、lcp、Gleason 和 pgg45 的前10个观察值具有相同的数字，只有一个例外：Gleason 的第三个观察值。为了确保这些特征作为输入特征确实可行，我们将 Gleason 变量转换为二分类变量，0 代表 6 分，1 代表 7 分或更高。代码如下：

1  prostate$gleason<-ifelse(prostate$gleason==6, 0, 1) table(prostate$gleason)

首先，建立训练数据集和测试数据集。因为已经有一个变量指示观察值是否属于训练集，所以我们可以使用 subset( )函数将 train 变量中 TRUE 的观察对象分配给训练集，将 train 变量中FALSE 的观察对象分配给测试集。还需要删除 “train”，因为我们不想用它作为预测变量。如下所示:

1  train <-subset(prostate, train ==TRUE)[, 1:9]str(train)test <-subset(prostate, train==FALSE)[,1:9]str(test)

岭回归模型

我们使用 glmnet 包构建岭回归模型。这个包要求输入变量存储在矩阵中，而不是数据集中。岭回归的要求是 glmnet（x = 输入矩阵，y = 响应变量，family = 分布函数，alpha = 0）。当alpha 为 0时，表示进行了岭回归；当 alpha 为 1 时，表示 LASSO 回归。为 glmnet 准备训练集数据也很容易，使用 as.matrix() 函数处理输入数据，并创建一个向量作为响应变量，如下所示:

1  x <-as.matrix(train[, 1:8]) y <-train[, 9]

现在我们可以创建岭回归模型。我们将结果保存在对象中，并给对象指定一个适当的名称，如 ridge。有一点非常重要，请务必注意：glmnet 包将在计算λ值之前首先对输入进行规范化，然后计算非规范化系数。因此，我们需要将响应变量的分布指定为高斯分布（正态分布），因为它是连续的。如下所示:

1  ridge <-glmnet(x, y, family =“gaussian”, alpha =0)

这个对象包含评估模型所需的所有信息。首先尝试 print() 函数，它会显示非零系数的数目，解释偏差的百分比和相应的 λ 值。程序包中算法的默认计算次数是 100，但是如果两个 λ 值之间的百分比增加不显著，则算法将在 100 次计算之前停止。也就是说，算法收敛到最优解。所有 λ 结果如下所示:

1  print(ridge)

以第 100 行为例。可见非零系数，也就是模型包含的变量数是 8，记住在岭回归中，这个数字是恒定的。还可以看到，解释偏差百分比为 0.6971，调谐系数 λ 的值为 0.08789。在这里，我们可以决定在测试集上使用哪个 λ。这个 λ 值应该是 0.08789，但是为了简单起见，我们可以在测试集上尝试 0.1。

在这一点上，一些图表非常有用。让我们看一下包中的默认图表。将 labe l= TRUE 以注释曲线，如下所示：

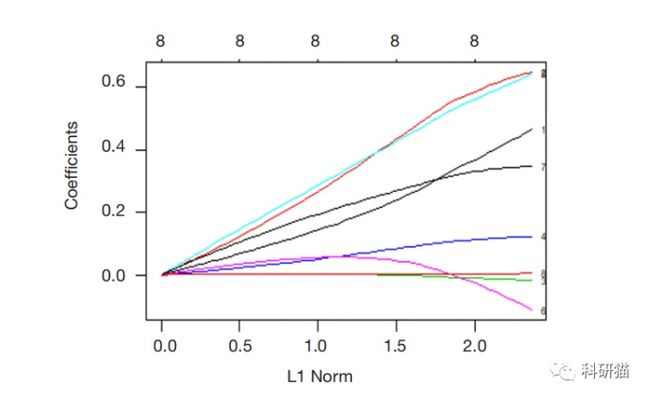
1  plot(ridge, label =TRUE)

在默认图表中，Y 轴是回归系数，X 轴是 L1 范数。系数和 L1 范数之间的关系如图所示。图形上方还有另一个 X 轴，其上的数字表示模型中的特征数。我们还可以看到系数是如何随λ变化的。只需使用 plot() 函数和参数 xvar=“lambda” 对其进行轻微调整。

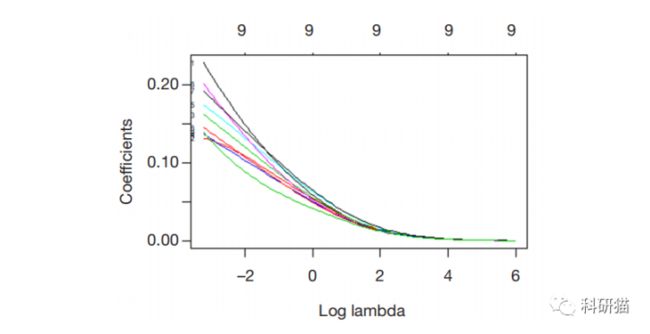
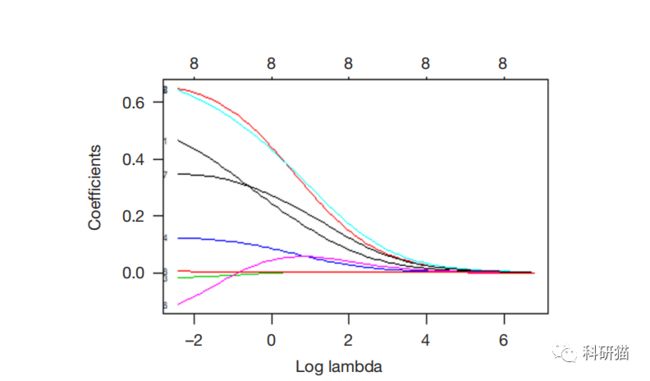
1  plot(ridge, xvar =“lambda”, label =TRUE)

此图显示，随着 λ 的减少，压缩参数减少，系数的绝对值增加。当λ为特定值时，我们还可以使用 predict() 函数查看系数值。如果我们想知道 λ 为 0.1 时系数的值，我们可以指定参数s = 0.1，指定 type=“coefficients”，当使用 glmnet() 来拟合模型时，我们应该使用特定的 glmnet值，而不是使用来自 λ 两边的值。具体如下：

1  ridge.coef<-predict(ridge, s=0.1, type =“coefficients”) ridge.coef

重要的是要注意，age、lcp 和 pgg45 变量的系数非常接近于零，但还不是零。别忘了看看偏差和系数之间的关系：

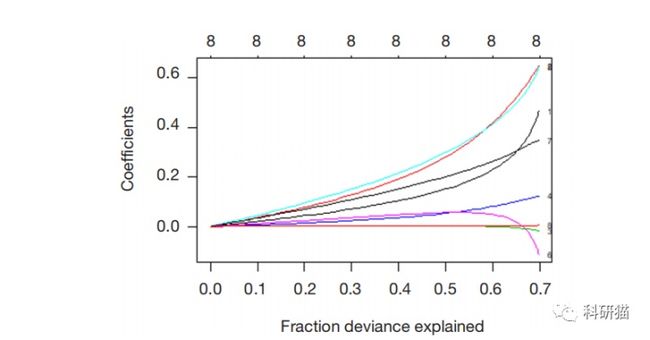
1  plot(ridge, xvar =“dev”, label =TRUE)

与前两张图相比，从这张图中我们可以看到，随着λ的减少，所解释的系数和分数偏差将会增加。如果 λ 值为 0，则将忽略收缩惩罚，并且模型将等同于 OLS。为了在测试集上证明这一点，我们需要先将测试集转换为矩阵：

1  newx<-as.matrix(test[, 1:8])

然后，我们使用 predict() 函数创建一个名为 ridge.y 的对象，指定 type=“response” 和 λ 值为 0.10。绘制表示预测值与实际值关系的统计图，如下图所示：

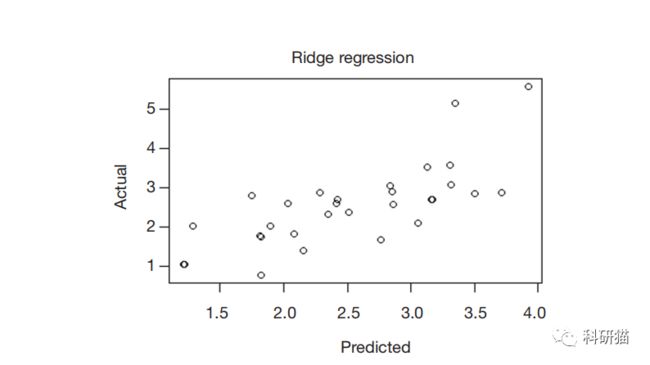
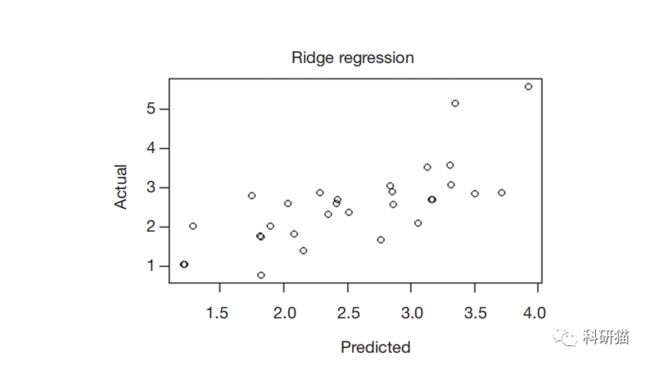
1  ridge.y =predict(ridge, newx =newx, type =“response”, s=0.1) plot(ridge.y , test$lpsa, xlab =“Predicted”, ylab =“Actual”, main =“Ridge Regression”)

下图显示了岭回归中预测值和实际值之间的关系。同样，在较大的 PSA 测量值中有两个有趣的异常值。在实际情况中，我们建议对异常值进行更深入的研究，以找出它们是否真的与其他数据不同，或者我们错过了什么。与 MSE 基准的比较可能会告诉我们一些不同的东西。我们可以先计算残差，然后再计算残差平方的平均值。岭回归分析均方差 = 0.4783559。

1  ridge.resid<-ridge.y-test$lpsa mean(ridge.resid^2)

小结

在这里，我们使用两个案例帮助大家了解岭回归模型。希望大家可以认识到正则化是一种提高计算效率和提取更多有意义特征的强大技术。合理使用岭回归和 LASSO 回归来构建准确的模型。

同名微信公众号联系客服领取代码和测试数据。

LASSO回归姊妹篇：R语言实现岭回归分析​mp.weixin.qq.com