Pytorch深度学习——处理多维度特征的输入（B站刘二大人P7学习笔记）

目录

1 模型的改变

1.1 采用Mini-Batch(N samples)的形式

2 代码的改变

2.1 构造一个多层的神经网络

2.2 代码的改变

2.2.1  数据集

2.2.2  定义多层次的神经网络函数

2.2.3  损失函数和优化器

2.2.4 训练函数

2.2.5 完整代码

---

      本节课以糖尿病病人的数据集为例展开，如图所示是糖尿病病人的数据集，其中X1~X8表示病人8项特征的详细数据，Y表示未来一年内糖尿病病人的病情是否会加重。而我们需要做的事情就是：根据数据集中的数据，利用深度学习，让机器能够自己判断Y的取值（1表示未来一年糖尿病会加重，0表示未来一年糖尿病不会加重）。

      X1~X8的值构成一个八维矩阵，Y构成一个一维矩阵，就完成输入的数据集。

      注：在数据库中的表，每一行表示一个记录，每一列表示一个字段；而在深度学习的数据集中，每一行表示一个分类，每一列表示一个特征。

---

1 模型的改变

       在之前的学习中，因为一个样本里只有一个特征，所以只用这单个特征值乘以权重在加上偏置量，输入Sigmoid函数中，即可得到一个0到1之间的数值；

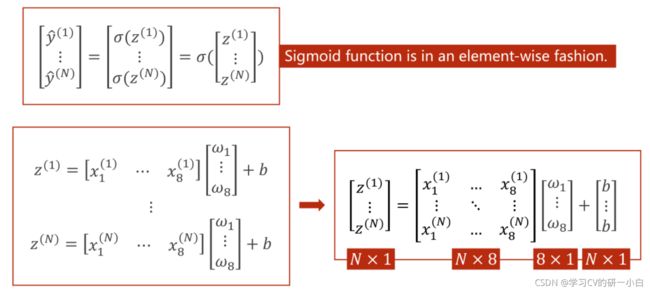
       但在本节课，一个样本里有八个特征，但计算的最终结果需要是一个实数，所以将样本中的每一个特征值都都和一个权重相乘再求和，再加一个偏置量 ，最后整体再录入到sigmoid函数中，获得  值。

1.1 采用Mini-Batch(N samples)的形式

       采用Mini-Batch的形式可以将方程运算转换矩阵的运算。

       为什么要把方程运算转换成矩阵运算？

       把方程运算转换成矩阵这种向量化的运算之后，可以利用计算机GPU/CPU的并行运算的能力来提高整个运算的速度。

 模型的改变：

       Pytorch提供的Sigmoid函数是一个按照向量内每个元素计算的函数（Sigmoid function is in an element-wise dashion.）

---

2 代码的改变

2.1 构造一个多层的神经网络

       神经网络层次叠加的过程，就是维度不断下降的过程。如下图所示，就是多层神经网络不断嵌套的过程：

        神经网络的本质：就是寻找一种最优的非线性的空间变换函数。而这种非线性的空间变换函数是通过多个线性变换层，通过找到最优的权重，组合起来的模拟的一种非线性的变化。

        为什么选择Sigmoid函数，因为激活函数（Sigmoid函数）可以将线性变换增加一些非线性的因子，这样我们就可以拟合一些非线性的变换。（如果每一层的神经网络只是不断的叠加线性函数的话，最终的函数还会只是一个线性函数。）

(神经网络并不是学习能力越强越好，学习能力太强，会学习数据集中的一些噪声，并不利于优化模型）

2.2 代码的改变

本例中并没有采用Mini-Batch的方法，依然采用的是full-batch。

2.2.1  数据集

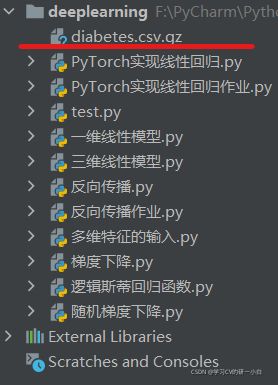
将糖尿病数据集为解压文件放在与代码同目录下，如下图：

数据集下载地址：链接：百度网盘 请输入提取码   提取码：vlfd

 具体代码如下：

xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype=np.float32)
# 取前8列
x_data = torch.from_numpy(xy[:, :-1])
# 取最后1列
y_data = torch.from_numpy(xy[:, [-1]])

2.2.2  定义多层次的神经网络函数

代码如下：

class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8, 6)
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 2)
        self.linear4 = torch.nn.Linear(2, 1)
        self.sigmoid = torch.nn.Sigmoid()

    def forward(self, x):
        # 注意所有输入参数都使用x
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        x = self.sigmoid(self.linear4(x))
        return x

model = Model()

2.2.3  损失函数和优化器

损失函数如下：

      损失函数依然采用交叉熵公式，但是需要取均值，所有reduction=‘mean’，课堂中老师讲的size_average=True 已经弃用。具体代码如下：

criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)

2.2.4 训练函数

具体代码如下：

for epoch in range(1000000):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())

    # 反馈
    optimizer.zero_grad()
    loss.backward()

    optimizer.step()

2.2.5 完整代码

import numpy as np
import torch
import matplotlib.pyplot as plt

xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype=np.float32)
# 取前8列
x_data = torch.from_numpy(xy[:, :-1])
# 取最后1列
y_data = torch.from_numpy(xy[:, [-1]])


class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8, 6)
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 2)
        self.linear4 = torch.nn.Linear(2, 1)
        self.sigmoid = torch.nn.Sigmoid()

    def forward(self, x):
        # 注意所有输入参数都使用x
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        x = self.sigmoid(self.linear4(x))
        return x


model = Model()

criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)

for epoch in range(1000000):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())

    # 反馈
    optimizer.zero_grad()
    loss.backward()

    optimizer.step()

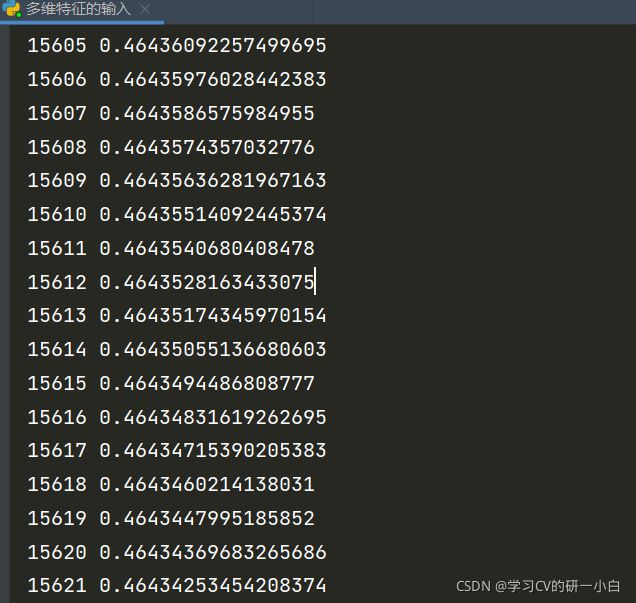
部分运行截图如下：